LeetCode-1206-设计跳表

不使用任何库函数，设计一个 跳表 。

跳表 是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

例如，一个跳表包含 [30, 40, 50, 60, 70, 90] ，然后增加 80、45 到跳表中，以下图的方式操作：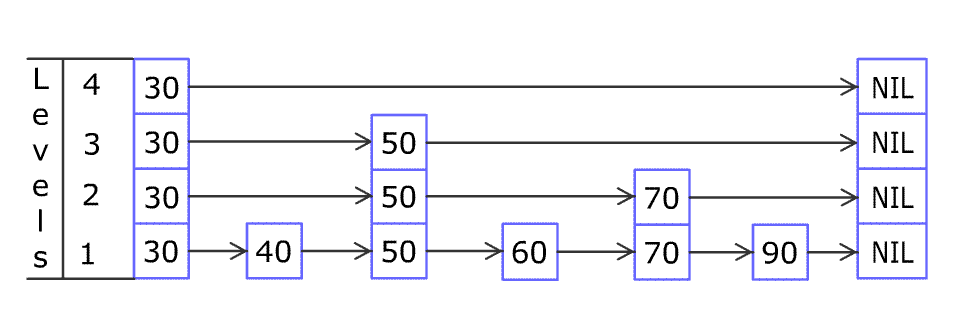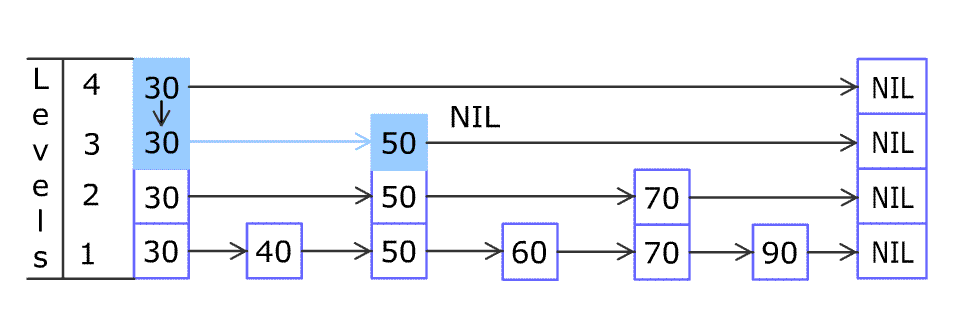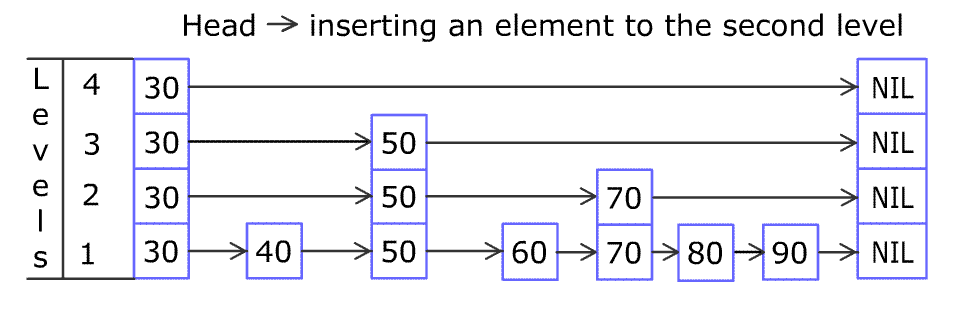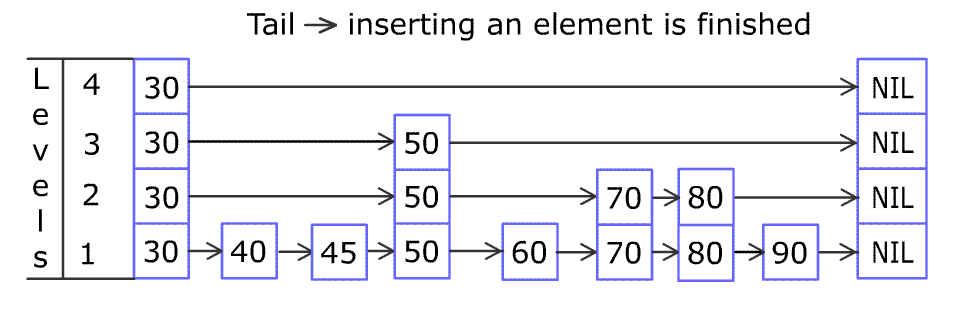

Artyom Kalinin [CC BY-SA 3.0], via Wikimedia Commons

跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

了解更多 : https://en.wikipedia.org/wiki/Skip_list

在本题中，你的设计应该要包含这些函数：

• bool search(int target) : 返回target是否存在于跳表中。
• void add(int num): 插入一个元素到跳表。
• bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回false. 如果存在多个 num ，删除其中任意一个即可。

注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

示例 1:

输入
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
输出
[null, null, null, null, false, null, true, false, true, false]

解释
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   // 返回 false
skiplist.add(4);
skiplist.search(1);   // 返回 true
skiplist.erase(0);    // 返回 false，0 不在跳表中
skiplist.erase(1);    // 返回 true
skiplist.search(1);   // 返回 false，1 已被擦除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

提示:

• 0 <= num, target <= 2 * 104
• 调用search, add, erase操作次数不大于 5 * 104

class Skiplist {
    class SkipNode {
        int val;
        /**
         * 每一个层级的指针
         */
        SkipNode[] next;

        public SkipNode(int val, int maxLevel) {
            this.val = val;
            this.next = new SkipNode[maxLevel];
        }
    }

    /**
     * 建立的调表所能达到的最高层级
     */
    private final int MAX_LEVEL = 32;
    /**
     * 概率因子
     */
    private final double SKIPLIST_P = 0.25;
    private SkipNode head;
    /**
     * 当前建立的最高层级
     */
    private int curLevel;

    public Skiplist() {
        head = new SkipNode(Integer.MIN_VALUE, MAX_LEVEL);
        curLevel = 0;
    }

    /**
     * 添加节点时, 该节点能达到的层数
     */
    private int getRandomLevel() {
        int level = 0;
        while (Math.random() < SKIPLIST_P && level < MAX_LEVEL) {
            level++;
        }
        return level;
    }

    /**
     * 从最高层级开始查找, 如果当前节点小于查找节点, 往右走, 否则往下走
     */
    public boolean search(int target) {
        SkipNode cur = head;
        for (int level = curLevel; level >= 0; level--) {
            // 找到第0层小于target的最大值
            while (cur.next[level] != null && cur.next[level].val < target) {
                cur = cur.next[level];
            }
        }
        // 指向下一个位置
        cur = cur.next[0];
        return cur != null && cur.val == target;
    }

    /**
     * 先找到每一个层级的小于 num 的最大节点, 即前继节点
     * 然后获取插入节点能到达的最高层级
     * 最后将 num 节点插入即可
     */
    public void add(int num) {
        SkipNode[] temp = new SkipNode[MAX_LEVEL];
        Arrays.fill(temp, head);
        SkipNode cur = head;
        // 找到所有层级的小于插入节点的最大节点
        for (int level = curLevel; level >= 0; level--) {
            // 找到第0层小于target的最大值
            while (cur.next[level] != null && cur.next[level].val < num) {
                cur = cur.next[level];
            }
            temp[level] = cur;
        }

        // 获取新插入节点所能达到的最高层级
        int randomLevel = getRandomLevel();
        SkipNode newNode = new SkipNode(num, randomLevel + 1);
        // 插入节点
        for (int i = 0; i <= randomLevel; i++) {
            newNode.next[i] = temp[i].next[i];
            temp[i].next[i] = newNode;
        }
    }

    /**
     * 先找到每一个层级的小于 num 的最大节点, 即前继节点
     * 然后判断是否存在该 num 节点, 不存在返回 false 即可
     * 存在则从第 0 层开始删除, 当某个层级找不到 num 节点时, 不需要继续往上层找
     * 判断删除 num 节点后, 最高层是否只剩下 head 节点, 如果是, 层级减一
     */
    public boolean erase(int num) {
        SkipNode[] temp = new SkipNode[MAX_LEVEL];
        Arrays.fill(temp, head);
        SkipNode cur = head;
        // 找到所有层级的小于插入节点的最大节点
        for (int level = curLevel; level >= 0; level--) {
            // 找到第0层小于target的最大值
            while (cur.next[level] != null && cur.next[level].val < num) {
                cur = cur.next[level];
            }
            temp[level] = cur;
        }

        cur = cur.next[0];
        if (cur == null || cur.val != num) {
            return false;
        }

        for (int i = 0; i <= curLevel; i++) {
            // 如果低层没有目标节点, 高层也不会有, 结束即可
            if (temp[i].next[i] != cur) {
                break;
            }
            temp[i].next[i] = cur.next[i];
        }

        if (curLevel > 0 && head.next[curLevel] == null) {
            curLevel--;
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126

指针版 有问题 日后修复

public class SkipNode<T> {
    int key;
    T value;
    SkipNode<T> right, down;
    public SkipNode(int key, T value) {
        this.key = key;
        this.value = value;
    }
}
1
2
3
4
5
6
7
8
9

public class SkipList<T> {
    /**
     * 头节点, 入口
     */
    private SkipNode<T> head;
    /**
     * 当前跳表索引层数
     */
    private int highLevel;
    /**
     * 用于投掷硬币
     */
    private Random random;
    /**
     * 最大层级
     */
    private final int MAX_LEVEL = 32;

    public SkipList() {
        random = new Random();
        head = new SkipNode<>(Integer.MIN_VALUE, null);
        highLevel = 0;
    }

    public SkipNode<T> search(int key) {
        SkipNode<T> cur = head;
        while (cur != null) {
            if (cur.key == key) {
                // 找到相应key
                return cur;
            } else if (cur.right == null || cur.right.key > key) {
                // 当前层次已经走到最后, 或者当前节点大于key, 往下层查找
                cur = cur.down;
            } else {
                // 右侧小于key
                cur = cur.right;
            }
        }
        return null;
    }

    public boolean erase(int key) {
        boolean res = false;
        SkipNode<T> cur = head;
        while (cur != null) {
            if (cur.right == null) {
                // 右边为空, 往下找
                cur = cur.down;
            } else if (cur.right.key == key) {
                res = true;
                // 删除当前层次的key节点, 继续往下一层找
                SkipNode<T> right = cur.right;
                cur.right = right.right;
                right.right = right.down = null;
            } else if (cur.right.key > key) {
                // 当前层级右侧不可能存在key节点
                cur = cur.down;
            } else {
                // 当前层级右侧节点小于key, 往右边找
                cur = cur.right;
            }
        }
        return res;
    }

    public void add(SkipNode<T> node) {
        int key = node.key;
        SkipNode<T> findNode = search(key);
        if(findNode != null) {
            //如果存在这个key的节点
            findNode.value=node.value;
            return;
        }
        SkipNode<T> cur = head;
        Stack<SkipNode<T>> stack = new Stack<>();
        // 找到每一个层级的待插入节点的左节点
        while (cur != null) {
            if (cur.right == null || cur.right.key > key) {
                // 如果右侧节点为空或者右侧节点的大于key节点, 往左走
                stack.add(cur);
                cur = cur.down;
            } else {
                // 右侧节点小于左侧节点, 往右走
                cur = cur.right;
            }
        }
        // 从第一层开始插入
        int level = 1;
        // 记录插入当前层级的插入节点, 以便在上一层插入时进行连接
        SkipNode<T> downNode = null;
        while (!stack.isEmpty()) {
            SkipNode<T> temp = stack.pop();

            // 创建新节点, 并连接新节点
            SkipNode<T> newNode = new SkipNode<>(node.key, node.value);
            newNode.down = downNode;
            // downNode记录当前节点
            downNode = newNode;
            if (temp.right == null) {
                temp.right = newNode;
            } else {
                newNode.right = temp.right;
                temp.right = newNode;
            }

            // 判断是否还需要向上插入
            if (level > MAX_LEVEL) {
                break;
            }
            // 概率插入
            if (random.nextDouble() > 0.5) {
                break;
            }
            level++;
            // 如果当前最大高度还要大(即新增了一层), 需要改变head节点
            if (level > highLevel) {
                highLevel = level;
                // 需要创建一个新的节点
                SkipNode<T> newHead = new SkipNode<>(Integer.MIN_VALUE, null);
                newHead.down = head;
                // 改变head
                head = newHead;
                stack.add(head);
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127