【通信原理】第三章 -- 随机过程[补充]

补充1：图解法求卷积

卷积定义

$$f_1(t)\ast f_2(t)={\int }_{-\infty }^{\infty }{f}_1(\tau )f_2(t-\tau )d\tau$$

卷积运算三步：翻转、分段平移、相乘积分

一个小例子

• 分析：

  1. f₁(t) -> f₁(τ)
  2. f₂(t) -> f₂(τ) -> f₂[-(τ - t)] 翻转并向右平移t个单位
  3. 相乘积分

• 结果：
  y ( t ) = { 0 , t < 0 ∫ 0 t A 2 d τ = A 2 t , 0 ≤ t ≤ T ∫ t − T T A 2 d τ = 2 A 2 T − A 2 t , T ≤ t ≤ 2 T 0 , t ≥ 2 T . y(t) =

  {0,t<0∫0tA2dτ=A2t,0≤t≤T∫t−TTA2dτ=2A2T−A2t,T≤t≤2T0,t≥2T" role="presentation" style="position: relative;">⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪0,∫t0A2dτ=A2t,∫Tt−TA2dτ=2A2T−A2t,0,t<00≤t≤TT≤t≤2Tt≥2T$$\{\begin{array}{ll}0,& t<0\\ {\int }_0^t{A}^{2}d\tau =A^{2}t,& 0\le t\le T\\ {\int }_{t-T}^T{A}^{2}d\tau =2A^{2}T-A^{2}t,& T\le t\le 2T\\ 0,& t\ge 2T\end{array}$$
  . y(t)=⎩ ⎨ ⎧​0,∫0t​A2dτ=A2t,∫t−TT​A2dτ=2A2T−A2t,0,​t<00≤t≤TT≤t≤2Tt≥2T​.

补充2：瑞利分布、莱斯分布、正态分布与均匀分布

均匀分布

• 也叫矩形分布，他是对称概率分布，在相同长度间隔的分布概率是等可能的
  f ( x ) = { 1 b − a , a < x < b 0 , o t h e r s f(x) =
  {1b−a,a<x<b0,others" role="presentation" style="position: relative;">⎧⎩⎨⎪⎪1b−a,0,a<x<bothers$$\{\begin{array}{ll}\frac{1}{b-a},& a<x<b\\ 0,& others\end{array}$$
  f(x)=⎩ ⎨ ⎧​b−a1​,0,​a<x<bothers​
  

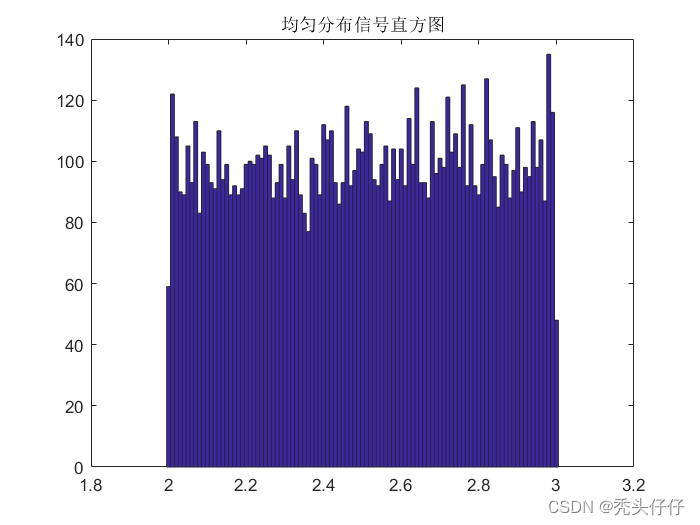
% 均匀分布
a=2;        % (a-b)均匀分布下限
b=3;        % (a-b)均匀分布上限
fs=1e7;     % 采样率，单位：Hz
t=1e-3;     % 随机序列长度，单位：s
n=t*fs;
hist(x,2:0.01:3);  % 输出信号的直方图
title('均匀分布信号直方图');
1
2
3
4
5
6
7
8

正态分布

• 正态分布也称“常态分布”，又名高斯分布
• 若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)
• 其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度
• 当μ = 0,σ = 1时的正态分布是标准正态分布
  $$f(x)=\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{{x-\mu }^2}{2{\sigma }^2})$$
  

% 正态分布
x = -10 : 0.01 : 10;
y = normpdf(x, 0, 1); %正态分布函数
figure;
axes1 = axes('Pos', [0.1 0.1 0.85 0.85]);
plot(x, y);
set(axes1, 'YLim', [-0.01 0.43], 'XLim', [-3, 3]);
1
2
3
4
5
6
7

瑞利分布

• 当一个随机二维向量的两个分量成独立的、有着相同的方差的正态分布时，这个向量的模成瑞利分布
• 瑞利分布式最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型
• 两个正交高斯噪声信号之和的包络服从瑞利分布
  $$f(x)=\frac{x}{{\sigma }^2}{e}^{-\frac{x^2}{2{\sigma }^2}},x>0$$
  

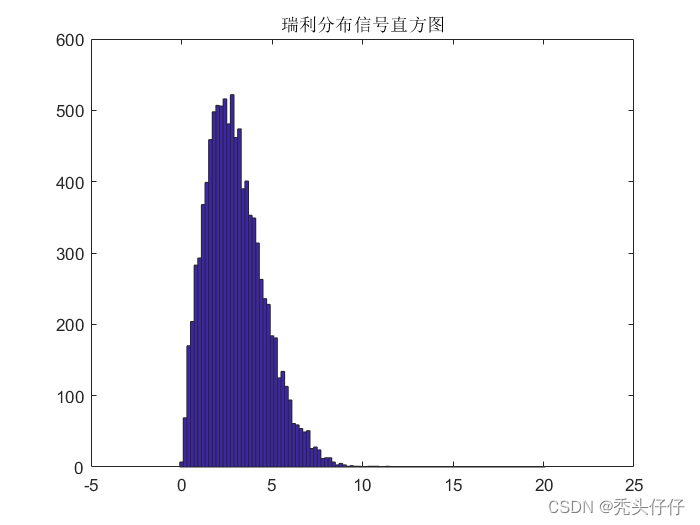
% 瑞利分布
sigma=2; % 瑞利分布参数sigma
fs=1e7;  % 采样率，单位：Hz
t=1e-3;  % 随机序列长度，单位：s
t1=0:1/fs:t-1/fs;
n=length(t1);
rand('state',0); % 把均匀分布伪随机发生器置为0状态
u=rand(1,n); % 产生（0-1）单位均匀信号
x=sqrt(2*log2(1./u))*sigma; % 广义均匀分布与单位均匀分布之间的关系
xlabel('t(单位:s)');
title('瑞利分布信号'); % 输出信号的直方图
hist(x,0:0.2:20);
title('瑞利分布信号直方图');
1
2
3
4
5
6
7
8
9
10
11
12
13

莱斯分布

• 实际上可以理解为主信号与服从瑞利分布的多径信号分量的和
• 在通信中，有一个信号站主要成分的噪声中，信道噪声一般呈现莱斯分布
  $$p(R)=\frac{R}{{\sigma }^2}exp(-\frac{R^2+A^2}{2{\sigma }^2})I_0(\frac{RA}{{\sigma }^2})$$

补充3：巴塞伐尔定理

• 能量信号能量 = 信号时域的能量 = 信号的频域不同频率分量的能量之和
  $$E={\int }_{-\infty }^{\infty }{s}^2(t)dt={\int }_{-\infty }^{\infty }|S(f){|}^{2}df$$

• 功率信号的功率 = 能量/无限大周期 = 对功率谱密度的无穷积分