-
2022深圳杯D题思路:复杂水平井三维轨道设计
题目描述
在油气田开采过程中,井眼轨迹直接影响着整个钻井整体效率。对于复杂水平井,较差的井眼轨迹很可能会造成卡钻或施加钻压困难等重大事故的发生。因而,在施工之前分析影响井眼轨迹走向规律的诸多因素,设计最适当的井眼轨迹显得十分重要。在井眼轨道设计模型中,设计轨道往往由一些连续的曲线构成。
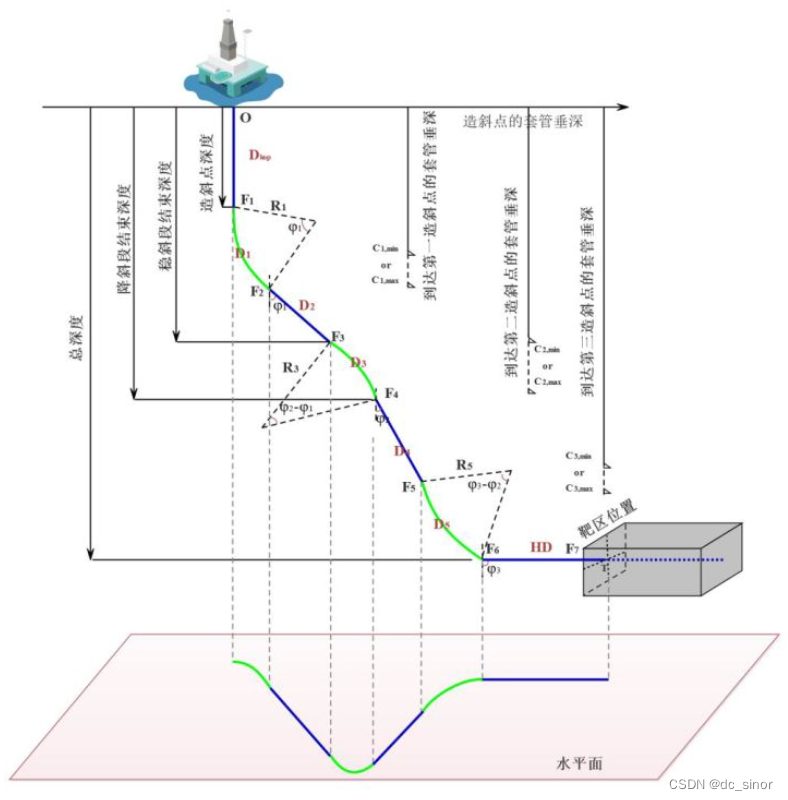
目前常用的复杂水平井的井眼轨道设计模型有“垂直段 + 增斜段 + 稳斜段 + 扭方位段 + 稳斜段 + 增斜段 + 水平段”的七段式井眼轨道设计模型,如图 1所示。描述井眼轨道的参数可分为基本测斜参数、坐标参数、挠曲参数和工艺参数,基本测斜参数包括井深、井斜角、方位角;坐标参数用来确定轨道上一点的空间位置,在空间直角坐标系下,空间坐标可由北坐标、东坐标和垂深表示 挠曲参数主要指井眼轨道的曲率、挠率等参数;工艺参数是指钻井施工中用来确定井眼轨道的参数,主要包括造斜点、工具造斜率和工具面角。七段式井眼轨道设计模型由空间上的圆弧(如增斜段、扭方位段)和直线(如垂直段、稳斜段)构成,相邻曲线、直线之间光滑 连接 。
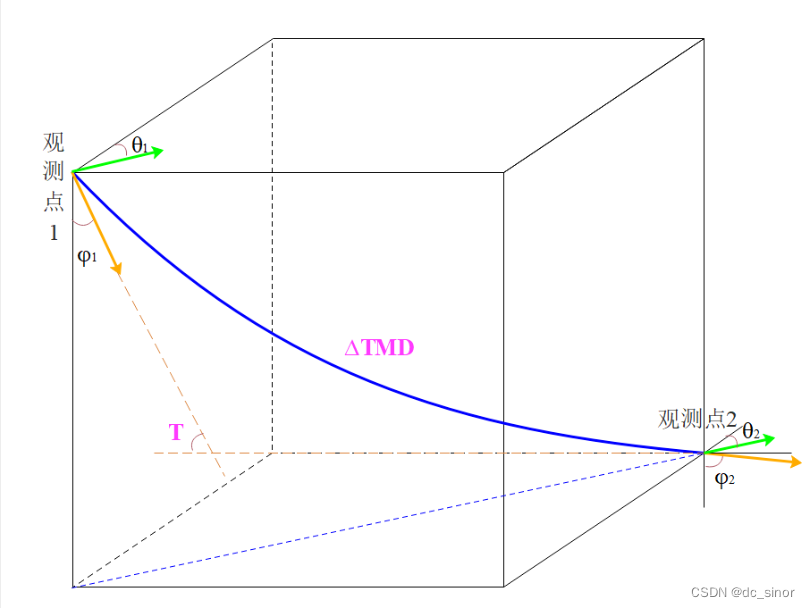
对于井眼轨道设计模型的每个井段,通过表征三维井眼轨道所需要 的特征参数将观测点 1到观测点 2处确定井眼轨道的形状和姿态,如图 2所示。图 2中所示井段是由观测点 1的方位角( 1)和井斜角 1)、观测点 2的方位角( 2)和井斜角 2)以及狗腿度( )征成。狗腿度为从井眼内的一点到另一点,井眼前进方向变化的角度。狗腿度既反映了井斜角度的变化,又反映了方位角度的变化。石油套管是用于支撑油、气井井壁的钢管,以保证完井后整个油井的正常运行。为此,套管坐封点应该位于合适的地层中,以便在固井后为套管鞋提供压力完整性。对于七段式井眼轨道设计模型,套管坐封点限制了井斜角的角 度。为此,在设计时需要考虑套管坐封点的影响,如图 1所示。
钻井公司作为采油厂的服务方,合理的完工验收标准是服务合同的要件。由于地层的复杂性,完全精准地按设计的井 眼轨道 完成钻井的可能性较小。如何平衡 钻井 成本 和 风险与完井采油的 方便 之间的冲突,提出一套合理的钻井完工验收标准也是本题目的任务 之一 。
请根据附录中的要求及相关参数建立模型解决以下问题:1、以井段为研究对象, 采用七段式井眼轨道设计模型, 结合井眼轨道优化设计参数范围表,确定理想的井眼轨道模型。
2、对于复杂水平井来说,当管柱在井眼轨道中上下移动时,就会产生阻力。小的阻力和扭矩有助于获得光滑的井眼轨道。 在 问 题 1的 基础上,考虑摩阻扭矩和阻力等情况下,确定理想的井眼轨道模型。
3、假设靶区窗口为长方形(如图 1所示),靶心位 于 窗口中心处。由于测量的影响,井眼轨道定位不可能绝对准确。因此, 在 问 题 2的 基础上,考虑命中率 的 情况,确定理想的井眼轨道模型。
4、通过平衡钻井成本和风险与完井采油的方便 之间的冲突,试提出一套合理的水平井钻井完工验收标准。
附录
-
为了计算扭矩和阻力,假设钻柱在轨道中以重型电缆的形式存在,忽略钻杆引起的管状刚度影响。计算只考虑钻柱旋转的状态,没有任何向上或向下的轴向运动。此外,钻柱的半径为 0.1英尺,重量为 0.3kN/英尺,摩擦系数为 0.2,浮力系数为 0.7。
-
假设靶区窗口为长方形, 窗口处的 靶心坐标由空间坐标表示为(5107.5,−3179,10875)(北坐标,东坐标和垂深 此外,目标区域的南北范围为 [3930,6284],目标区域的东西范围为 [−3228,−3130],目标区域的垂深为[−10900,−10850]。 此外,井眼轨道末端与靶区窗口垂直。
-
表 1为井眼轨道优化设计参数范围表。
思路-建模过程
画出受力分析图如下,i代表第i段
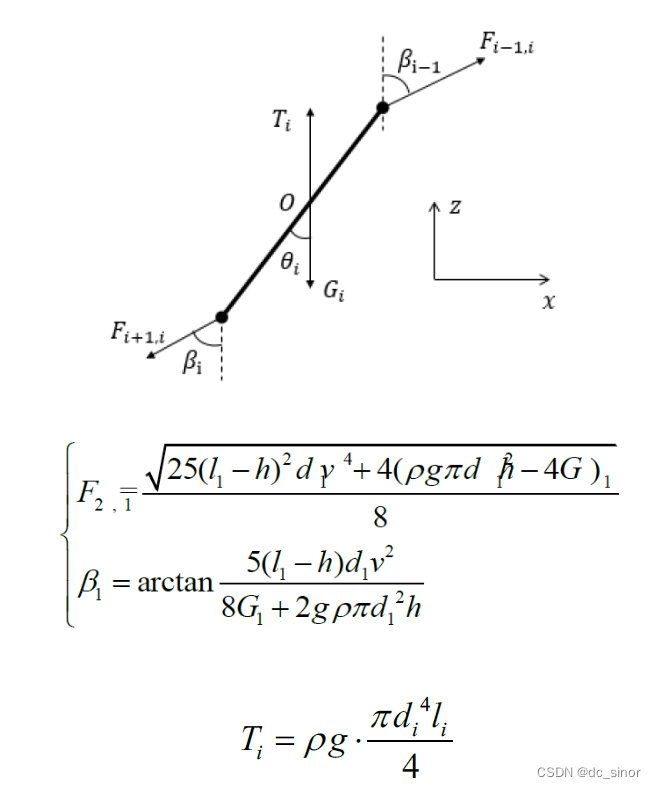
求解方程组分离变量得到第i段与第i-1段之间作用力递推关系式为:
继续推导,并加入约束条件,得到:对于系统状态模型的求解,难以直接通过大量状态方程得到定解,所以联立非线性方程组求定解方法不适用。因此本文采用一种基于最小二乘思想的循环搜索算法对模型进行求解。
基于最小二乘思想的循环搜索算法
对于定步长的循环搜索算法,误差的主要来源为变量的步长,因此可以通过减小步长,根据最优解变化幅度来判断步长是否合理。取变量h 步长没原步长的1/50,则算法精度应提高50 倍,定义相对优化量q 为目标函数优化量与理论优化量的比值:
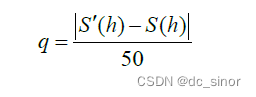
function [x,minf]=minMGN(f,x0,var,eps) format long if nargin==3 eps=1.0e-6; end S=transpose(f)*f; %函数S的梯度 k=length(f); n=length(x0); x0=transpose(x0); tol=1; A=jacobian(f,var); %函数f的梯度 while tol>eps Fx=zeros(k,1); for i=1:k Fx(i,1)=Funval(f(i),var,x0); end Sx=Funval(S,var,x0); Ax=Funval(A,var,x0); gSx=transpose(Ax)*Fx; %函数S当前的梯度值 dx=-transpose(Ax)*Ax\gSx; %自变量增量 alpha=1; while 1 S1=Funval(S,var,x0+alpha*dx); S2=Sx+2*(1.0e-5)*alpha*transpose(dx)*gSx; if S1>S2 alpha=alpha/2; %参数修正 continue; else break; end end x0=x0+alpha*dx; tol=norm(dx); end x=x0; minf=Funval(S,var,x); format short;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
通过matlab编程计算可得,由于长度范围在0.1 数量级,因此q 可以忽略不计,故目前搜索算法中设置的步长可认为是合理的。
套管系统优化模型的建立
目标函数
本文一共确立如下3 个优化目标:
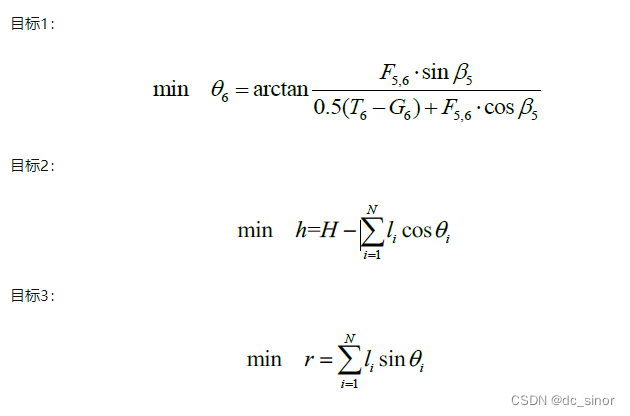
约束条件
根据附表数据可直接写出:
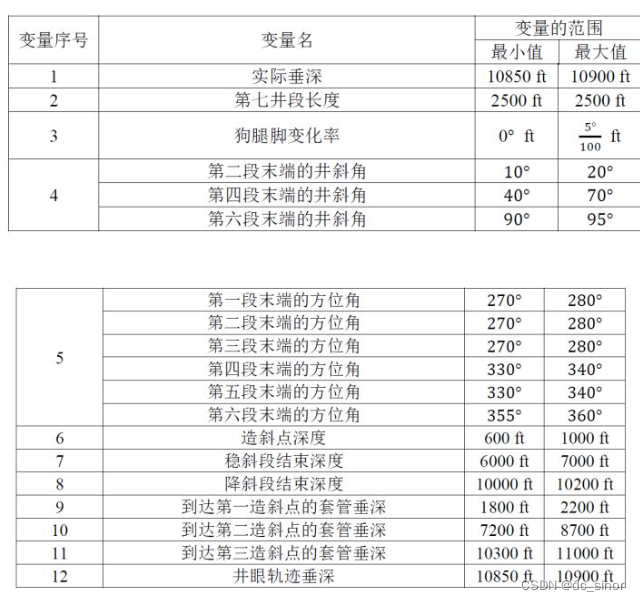
最终的优化模型如下:

模型求解
多目标转化单目标求解
对于三个目标的权重值的确定,基于赋权的可靠性考虑,本文在此选择了主观性相对较小,能够充分利用数据特征的熵权法。熵权法可以根据各个目标的变异度,利用信息熵计算出各个目标的客观权重值。信息熵越小,变异程度最大,重要程度越大。期计算结果为A =11.46, B=1.5,C= 0.05。接着我们对以上三个目标分别赋以权重,A B C ,将多目标优化转化为单目标优化问题,用U 表示总的优化目标:
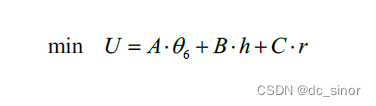
熵权法代码如下:function [s,w]=shang(x,ind) %实现用熵值法求各指标(列)的权重及各数据行的得分 %x为原始数据矩阵, 一行代表一个样本, 每列对应一个指标 %ind指示向量,指示各列正向指标还是负向指标,1表示正向指标,2表示负向指标 %s返回各行(样本)得分,w返回各列权重 [n,m]=size(x); % n个样本, m个指标 %%数据的归一化处理 for i=1:m if ind(i)==1 %正向指标归一化 X(:,i)=guiyi(x(:,i),1,0.002,0.996); %若归一化到[0,1], 0会出问题 else %负向指标归一化 X(:,i)=guiyi(x(:,i),2,0.002,0.996); end end %%计算第j个指标下,第i个样本占该指标的比重p(i,j) for i=1:n for j=1:m p(i,j)=X(i,j)/sum(X(:,j)); end end %%计算第j个指标的熵值e(j) k=1/log(n); for j=1:m e(j)=-k*sum(p(:,j).*log(p(:,j))); end d=ones(1,m)-e; %计算信息熵冗余度 w=d./sum(d); %求权值w s=100*w*X'; %求综合得分- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
-
-
相关阅读:
SAP MASS增加PR字段-删除标识
使用Go语言交叉编译开发嵌入式Linux应用程序
18.2 使用NPCAP库抓取数据包
前端解决跨域 3 种方法 -对接读卡器时出现跨域问题
【数据挖掘】XGBoost面试题:与GBDT的区别?为什么使用泰勒二阶展开?为什么可以并行训练?为什么快?防止过拟合的方法?如何处理缺失值?
C++:stl_List的介绍与模拟实现
Android NDK之使用 arm-v7a 汇编实现两数之和
代理流量卡到底能赚钱吗?行业老司机带你深入了解。
【C语言进阶】动态内存管理常见错误
每日亿题之20220904
- 原文地址:https://blog.csdn.net/dc_sinor/article/details/125989304
