• stm32F407-------DSP学习

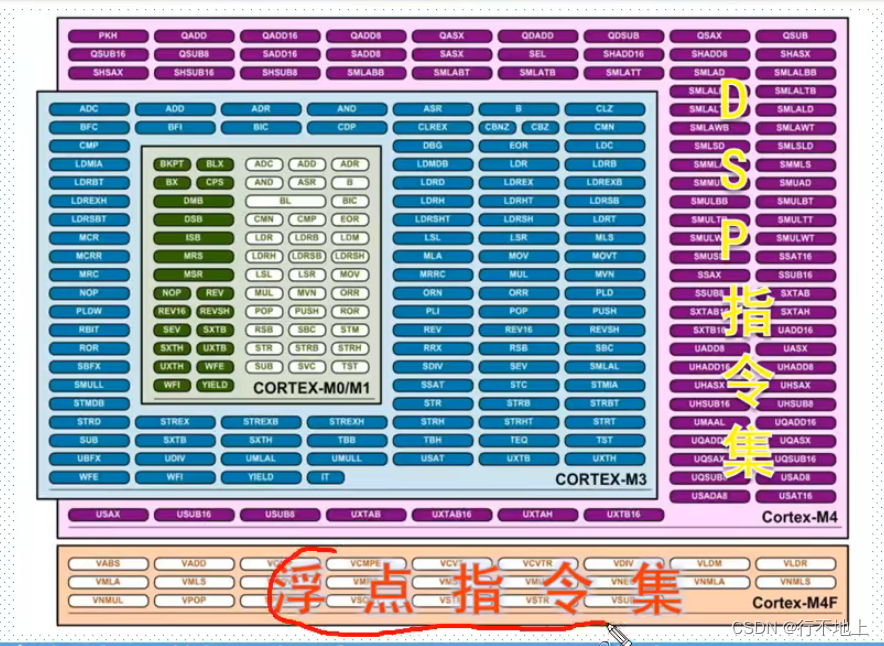
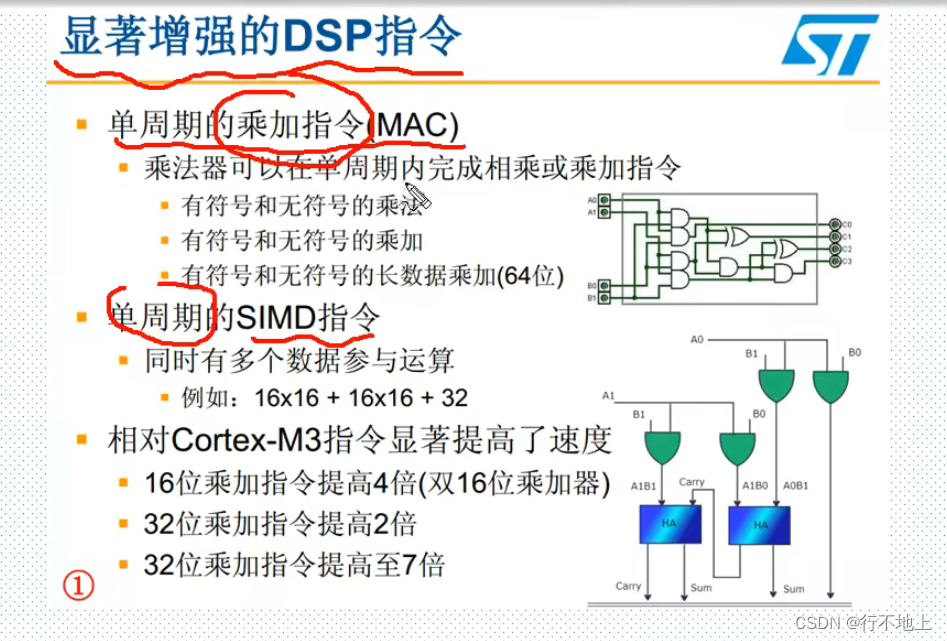
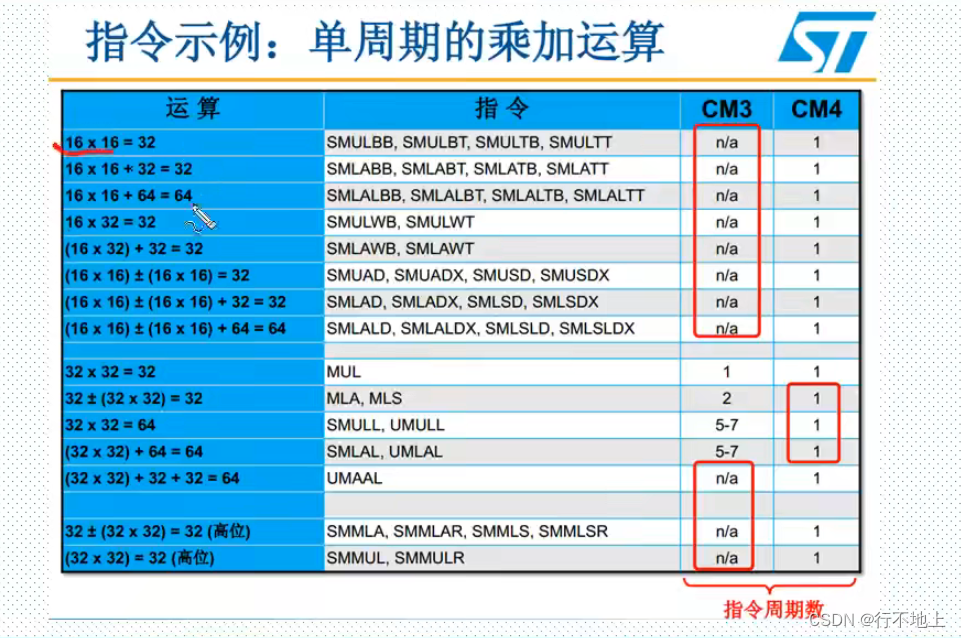
     DSP源码库介绍：

     

     DSP库运行环境搭建：

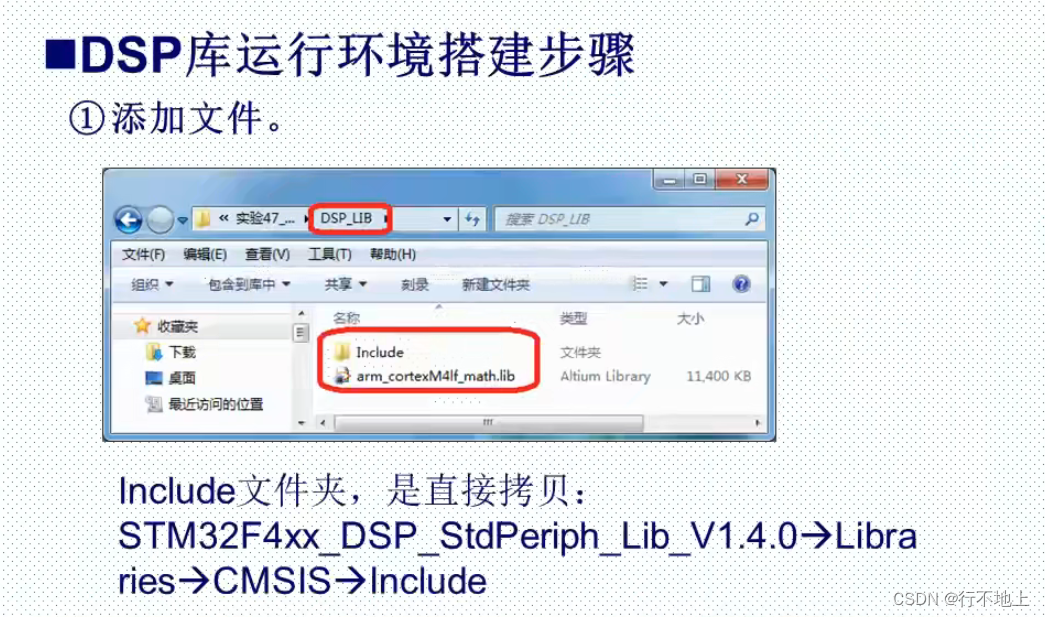
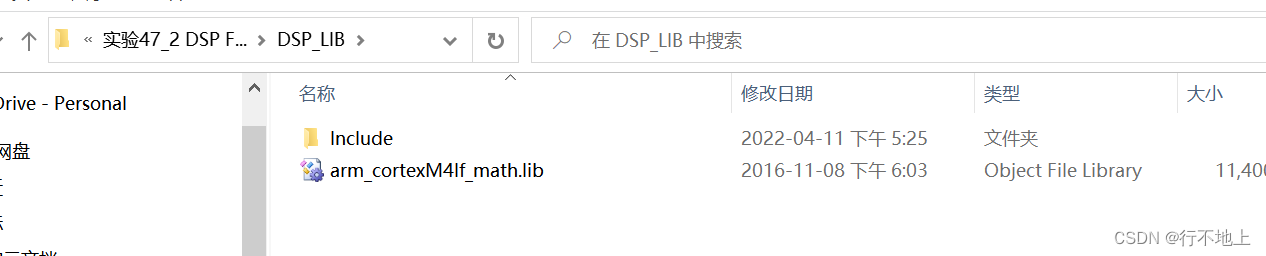
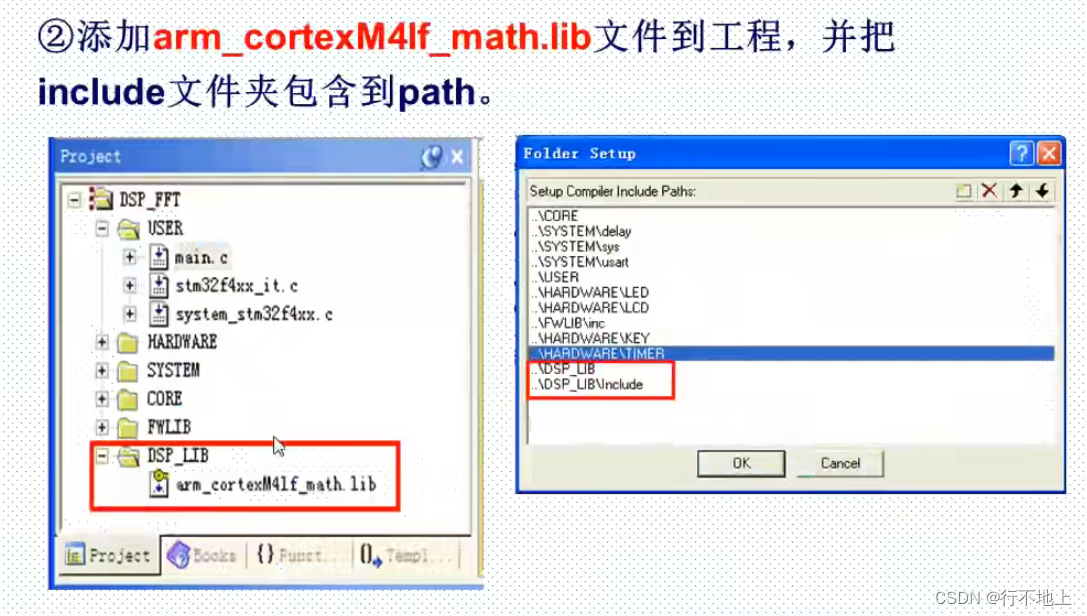
    （ALL FILES）

    STM32F40_41xxx,USE_STDPERIPH_DRIVER,ARM_MATH_CM4,__CC_ARM,ARM_MATH_MATRIX_CHECK,ARM_MATH_ROUNDING

    DSP库测试：

    1、BasicMath测试：

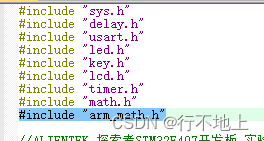         #include "arm_math.h"  

     2、DSP_FFT测试：

            首先，我们简单介绍下 FFT ： FFT 即快速傅里叶变换，可以将一个时域信号变换到频域。
            因为有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了，这就是很多信号分析采用 FFT 变换的原因。另外， FFT 可以将一个信号的频谱提取出来，
    这在频谱分析方面也是经常用的。简而言之， FFT 就是将一个信号从时域变换到频域方便我们
    分析处理。
            在实际应用中，一般的处理过程是先对一个信号在时域进行采集，比如我们通过 ADC ，按
    照一定大小采样频率 F 去采集信号，采集 N 个点，那么通过对这 N 个点进行 FFT 运算，就可
    以得到这个信号的频谱特性。
            这里还涉及到一个采样定理的概念：在进行模拟/ 数字信号的转换过程中，当采样频率 F 大
    于信号中最高频率 fmax的 2 倍时(F>2*fmax)，采样之后的数字信号完整地保留了原始信号中的信
    息，采样定理又称奈奎斯特定理。举个简单的例子：比如我们正常人发声，频率范围一般在 8KHz
    以内，那么我们要通过采样之后的数据来恢复声音，我们的采样频率必须为 8KHz 的 2 倍以上，
    也就是必须大于 16KHz 才行。
            模拟信号经过 ADC 采样之后，就变成了数字信号，采样得到的数字信号，就可以做 FFT
    变换了。 N 个采样点数据，在经过 FFT 之后，就可以得到 N 个点的 FFT 结果。为了方便进行
    FFT 运算，通常 N 取 2 的整数次方。
            假设采样频率为 F ，对一个信号采样，采样点数为 N ，那么 FFT 之后结果就是一个 N 点
    的复数，每一个点就对应着一个频率点（以基波频率为单位递增），这个点的模值（ sqrt( 实部 2 +
    虚部 2 ) ）就是该频点频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信
    号的峰值为 A ，那么 FFT 的结果的每个点（除了第一个点直流分量之外）的模值就是 A 的 N/2
    倍，而第一个点就是直流分量，它的模值就是直流分量的 N 倍。
            这里还有个基波频率，也叫频率分辨率的概念，就是如果我们按照 F 的采样频率去采集
    一个信号，一共采集 N 个点，那么基波频率（频率分辨率）就是 f k =F/N 。这样，第 n 个点对应
    信号频率为： F*(n-1)/N ；其中 n ≥ 1 ，当 n=1 时为直流分量。
            关于 FFT 我们就介绍到这。
            如果我们要自己实现 FFT 算法，对于不懂数字信号处理的朋友来说，是比较难的，不过，
    ST 提供的 STM32F4 DSP 库里面就有 FFT 函数给我们调用，因此我们只需要知道如何使用这些
    函数，就可以迅速的完成 FFT 计算，而不需要自己学习数字信号处理，去编写代码了，大大方
    便了我们的开发。
            STM32F4 的 DSP 库里面，提供了定点和浮点 FFT 实现方式，并且有基 4 的也有基 2 的，
    大家可以根据需要自由选择实现方式。注意：对于基 4 的 FFT 输入点数必须是 4 n ，而基 2 的
    FFT 输入点数则必须是 2 n ，并且基 4 的 FFT 算法要比基 2 的快。
            第一个函数 arm_cfft_radix4_init_f32 ，用于初始化 FFT 运算相关参数，其中： fftLen 用于指定 FFT 长度（ 16/64/256/1024/4096 ），本章设置为 1024 ； ifftFlag 用于指定是傅里叶变换 (0) 还是反傅里叶变换(1) ，本章设置为 0 ； bitReverseFlag 用于设置是否按位取反，本章设置为 1 ；最后，所有这些参数存储在一个 arm_cfft_radix4_instance_f32 结构体指针 S 里面。 
    1.   arm_cfft_radix4_instance_f32 scfft;
    2.  
    3.   arm_cfft_radix4_init_f32(&scfft,FFT_LENGTH,0,1);//初始化scfft结构体，设定FFT相关参数
            第二个函数 arm_cfft_radix4_f32 就是执行基 4 浮点 FFT 运算的， pSrc 传入采集到的输入信
    号数据（实部 + 虚部形式），同时 FFT 变换后的数据，也按顺序存放在 pSrc 里面， pSrc 必须大
    于等于 2 倍 fftLen 长度。另外， S 结构体指针参数是先由 arm_cfft_radix4_init_f32 函数设置好，
    然后传入该函数的。 
    arm_cfft_radix4_f32(&scfft,fft_inputbuf);	//FFT计算（基4）
            第三个函数 arm_cmplx_mag_f32 用于计算复数模值，可以对 FFT 变换后的结果数据，执行
    取模操作。 pSrc 为复数输入数组（大小为 2*numSamples ）指针，指向 FFT 变换后的结果； pDst
    为输出数组（大小为 numSamples ）指针，存储取模后的值； numSamples 就是总共有多少个数
    据需要取模。 
    arm_cmplx_mag_f32(fft_inputbuf,fft_outputbuf,FFT_LENGTH);	//把运算结果复数求模得幅值
            通过这三个函数，我们便可以完成 FFT 计算，并取模值。本节例程（实验 47_2 DSP FFT
    测试）同样是在 52.1.2 节已经搭建好 DSP 库运行环境上面修改代码，只需要修改 main.c 里面
    的代码即可，本例程 main.c 代码如下：
            以上代码只有一个 main 函数，里面通过我们前面介绍的三个函数： arm_cfft_radix4_init_f32、 arm_cfft_radix4_f32 和 arm_cmplx_mag_f32 来执行 FFT 变换并取模值。每当按下 KEY0 就会重新生成一个输入信号序列，并执行一次 FFT 计算，将 arm_cfft_radix4_f32 所用时间统计出来，显示在 LCD 屏幕上面，同时将取模后的模值通过串口打印出来。
            这里，我们在程序上生成了一个输入信号序列用于测试，输入信号序列表达式：
            通过该表达式我们可知，信号的直流分量为 100 ，外加 2 个正弦信号和一个余弦信号，其
    幅值分别为 10 、 30 和 50 。

  • 相关阅读:
    使用 ModSecurity 和 ELK 进行持续安全监控
    计算机网络八股文复习
    详谈判断点在多边形内的七种方法
    vue3+element-plus props中的变量使用 v-model 报错
    QT c++ 将浮点数数组转换成 QByteArray
    1558. 得到目标数组的最少函数调用次数
    spring创建bean的三种方式
    输入M*N阶矩阵A和B，用函数编程计算并输出A与B之和
    Linux学习-38-硬盘分区命令fdisk介绍
    flutter 阿里云上传文件
  • 原文地址：https://blog.csdn.net/qq_53889131/article/details/125983021