leetcode：1838. 最高频元素的频数【排序 + 前缀和 + 二分 + 思维】

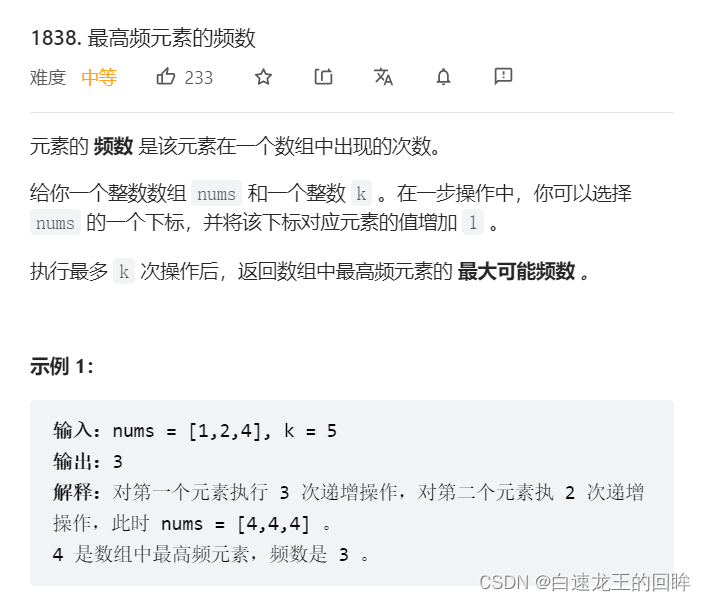
分析

由于只能通过加得到某个频数
因为求的是频数，所以二分频数
频数也作为自变量，而最少操作次数成为了因变量
问题的关键就是在给定频数的情况下，求出最少操作数
因为频数越大的话，最少操作数肯定是越大的

那么，我们可以假设，最大频数的数一定是num中的（很直觉），我们假设当前的频数是appears
然后给nums排序，最贪心的选法就是在在长度为appear的[ai, aj]中计算操作数
而这个操作数很显然就是(appears - 1) * aj - Sum([ai, aj - 1])因此需要前缀和
这样找到最少的那组区间即为给定频数的最小操作数

ac code

class Solution:
    def maxFrequency(self, nums: List[int], k: int) -> int:
        n = len(nums)
        nums.sort()
        # Sum[L, R] => preSum[R + 1] - preSum[L]
        preSum = list(accumulate(nums, initial = 0))
        

        def get_ops(appears):
            if appears == 1:
                return 0
            ops = inf
            for i in range(n - appears + 1):
                # [ai, aj] 共k个
                first, last = i, i + appears - 1
                # up to last: (appears - 1) * alast - Sum(afirst ... alast - 1)
                op = (appears - 1) * nums[last] - (preSum[last] - preSum[first])
                ops = min(ops, op)
            return ops
        
        l, r = 1, 10 ** 5
        while l + 1 < r:
            mid = l + (r - l) // 2
            if get_ops(mid) > k:
                r = mid - 1
            else:
                l = mid
        
        for ans in range(r, l - 1, -1):
            if get_ops(ans) <= k:
                return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

总结

还是回归套路
要求哪个东西就对它二分，然后以它为自变量，有限制的东西为因变量构造函数
结合排序或前缀和的技术加快速度即可，注意关注样例的特点