NR Modulation 5 - 码农知识堂

NR Modulation 5
参考

Professor David S. Ricketts

目录
1. Quadrature Amplitude Modulation
2. cos vs sin
一 Quadrature Amplitude Modulation

1.1 优点：提高了带宽效率

1.2 影响因素：

抗噪性以及功率

1.3 星座图

星座图有很多种

主要看

1：任意两点之间的最小距离

影响抗噪声性能，距离越小越容易出错

2：最大距离

影响功率，越大功耗越高

1.4 例子

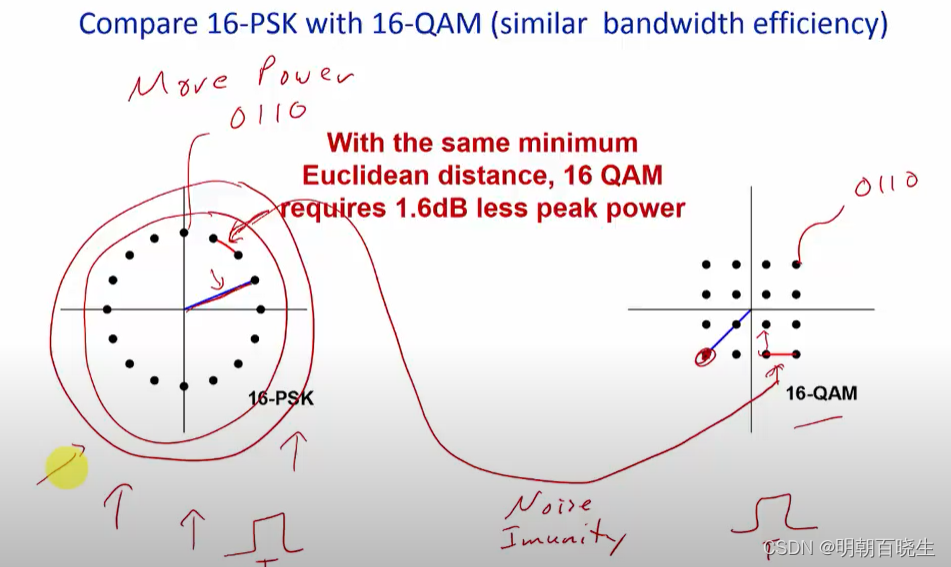
如下 16-PSK 16-QAM

一个symbols 都是传输4bit,带宽效率一致

但是16-PSK 功耗更高。实际使用中，没有哪个是更好的，比如有效硬件限制，

在高频信号时候，AM调制效率非常差，这个时候使用16-PSK会比

16-QAM更好

二 cos vs sin

2.1 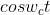  I

定理1：狄拉克函数重要性质

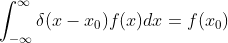
$\int_{-\infty}^{\infty}\delta(x-x_0)f(x)dx=f(x_0)$

定理2：傅里叶逆变换定义

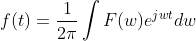
$f(t)=\frac{1}{2\pi}\int F(w)e^{jwt}dw$

根据定理1,2 对 $2\pi \delta (w-w_c)$ 做傅里叶逆变换

   $\frac{1}{2\pi}\int_{-\infty}^{\infty} 2\pi \delta (w-w_c) e^{jwt}dw=\frac{2\pi}{2\pi}e^{jw_c}=e^{jw_ct}$ （t是常量）

则

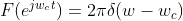
$F(e^{jw_c t})=2\pi \delta (w-w_c)$

因为

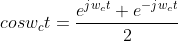
$cos w_c t= \frac{e^{j w_c t}+e^{-j w_c t}}{2}$

   $=\frac{2\pi \delta (w-w_c)+2\pi \delta (w+w_c)}{2}$

   $=\pi(\delta (w-w_c)+\delta (w+w_c))$

时域上乘以一个cos函数本质上相当于频域上的卷积，卷积利用狄拉克函数的性质

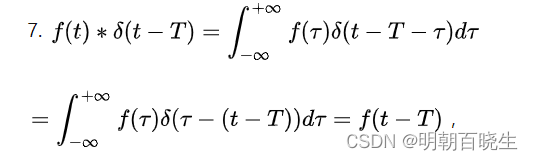
利用上面性质假设输入信号为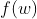,则最后的输出信号s(w)就是，得到的就是最后一张图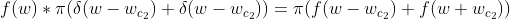

   $f(w)*\pi(\delta(w-w_{c_2})+\delta(w-w_{c_2}))=\pi(f(w-w_{c_2})+f(w+w_{c_2}))$

2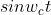.2  Q

实际上差不多，多了一个j

2.3 quadrature modulation

最后看一下IQ 调制，一路是跟cos 卷积，一路跟sin 卷积

卷积后的包络如右图.

三 cos vs sin

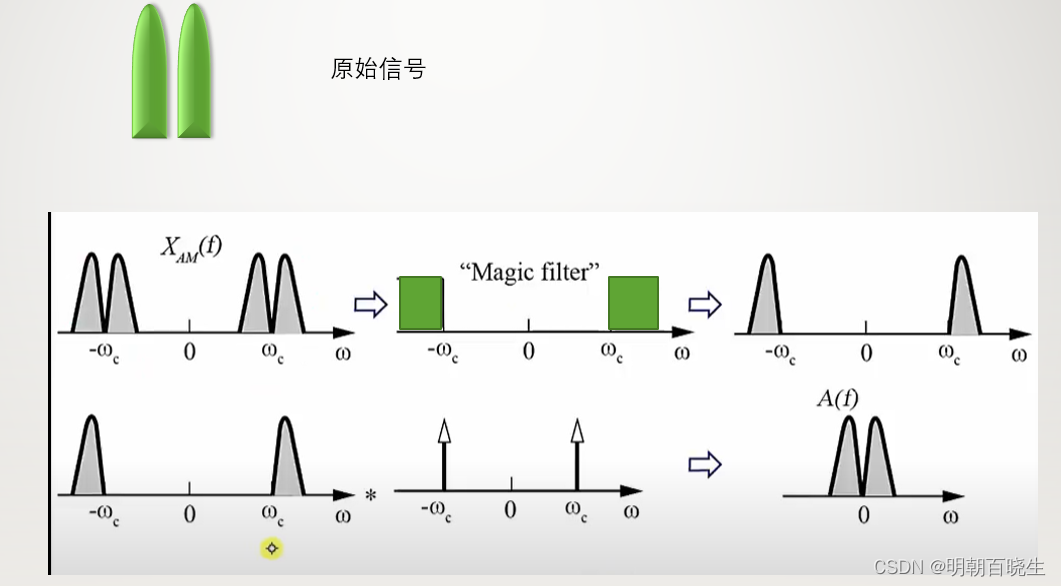
我们原始发送的信号,经过变换后变成了4份copy.

可以通过一个滤波器把重复的部分过滤掉，降低功率。

3.1 cos vs sin

$cos wt =\frac{e^{jwt}+e^{-jwt}}{2}$
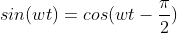
   $sin(wt)=cos(wt-\frac{\pi}{2})$

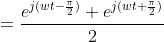
   $=\frac{e^{j(wt-\frac{\pi}{2})}+e^{j(wt+\frac{\pi}{2})}}{2}$

   $=\frac{-je^{jwt}+je^{-jwt}}{2}$

   $=\frac{e^{jwt}-e^{-jwt}}{2j}$

3.2 再看一下

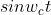
<0部分相当于乘以一个j,做了翻转

>0 部分乘以一个-j,保持不变
相关阅读:
Android Java 多线程常见问题
 2021 中国系统java面试笔试题（含面试题解析）
vscode_pytest_配置debug环境:增加和打印环境变量
 不愧是阿里内部 Spring Boot 笔记，从头到尾不讲废话
 如何在opensuse build service (obs)打包deb包用于分发各个发行版
 淘宝/天猫API：item_password-获得淘口令真实url
【shell 特殊字符】
第3章定义内存缓存和log4net日志中间件
 2022年6月深圳PMP®项目管理认证招生简章
 C++入门第八篇---STL模板---list的模拟实现
原文地址：https://blog.csdn.net/chengxf2/article/details/125907648