前言： 

对于2022年来说，自己一直是处在一个比较焦虑的状态当中，而这个状态在我的写博客的量中就可以很明显的体现了：

而2022年的1月那会状态其实没有发生变化，一切的一切在于年后的2月中下旬，组织架构调整了，这块其实在小程序高级电商前端第2周深入理解REST API开发规范 开启三端分离编程之旅<二>----scroll-view组件的灵活应用、async和await问题探讨、spu-scroll自定义组件、Lin UI Price价格组件应用、css编写原则 密码保护写这篇时就已经说过了，也就是在这之后的半年里有效篇数就3篇。。当一个人在规律地在做着某些事时，突然间规律不见了，那说明这个人的心态大概率是因为某些事发生了巨大的变化，是的，我今年的心态就处于这种变化的状态，其中最大的一个原因是公司的各种考核让你没有太多时间来写博客了，因为考核不通过的直接结果就是末尾淘汰，当面对这种压力时，其实就是两种心态：一是摆烂、二是努力让自己不被淘汰。那很明显大多数人肯定是不会主动在这“疫情”期间来放弃收益来源对吧，所以为了不让自己被淘汰就得平常花时间来准备考核的内容，其中大学数学是一个重点考试内容【种种的抱怨就不多说了，需要有正能量】，其实在去年就为了应付考试学习了大学数据的线性代数部分：

但是“高等数学”、“概率论与数量统计”这两个方向缺失，最近一直基于网上的教程在恶补，高等数学的基本“看完”了，其中“看完”俩字加引号，嗯，仅仅就走马观花式地看，没有任何输出，因为“快”嘛，感觉又回到了N年前非常浮躁非常飘的状态了，所以决定还是要有输出，摈弃浮躁，于是才有了此篇的想法，希望自己能够坚持下来，当职场遇到逆境时，尽量想办法让压力化为动力，而不是一味的抱怨和逃避，因为抱怨只会让自己整天活在阴霾当中越陷越深，当这种逆境中的动力产生之后，你在职场就会变得更加的抗跌，正能量也会充满其身，所以，今年其它的学习计划被打断了木关系，我先开个专栏把高数这个先好好落实，毕竟要事为先，人生其实也就是被各种惊喜意外给充斥着，既来之则安之。

好，心灵鸡汤就不撒了，我发现对于程序员而言，如果当你发现自己每天都过得非常焦虑，建议可以先从写博客开始，让自己先静下来，写得好与不好其实不重要，重要的是通过慢写来让自己能沉下心来。。。。不撒了，回到正题，这里的高数学习选的是普林斯顿微积分读本，也就是长这样：

至于为啥选它就不过多说了，反正从目录来看貌似适合初学者，下面正式开始。 

函数：

关于函数的定义应该都比较熟了，尤其对于程序员的我们，这里主要是当一个复习吧，拿书中的一句话可以很好的说明为啥要把函数学好：
“不借助函数却想去做微积分，这无疑是你所做的最无意义的事情之一。”

定义：

初步理解：

在数学里是这么定义函数的，“函数是将一个对象转化为另一个对象的规则，起始对象称为输入，来自称为定义域的集合。返回对象称为输出，来自称为上域的集合。”

说实话这定义有点模糊，其实从程序员的角度对于函数的理解就是：“有一个输入参数，通过调用某函数，最终再有个输出”，当然这里不能完全按程序员的思想来理解，毕竟对于void的函数是木有输出的。

对于数学定义的函数，拿一个简单的函数来理解：y = f(x)，其中x为输入，它的值是来自于定义域的集合，那啥叫定义域呢？给个例子就明白了：

好，继续理解，对于y= f(x)中的y来说其实就是函数定义中的输出， 它的值是来自上域的集合，那啥叫上域呢？这块在下面就会进行说明，先不必过多地操心。

进一步理解定义：

由于函数是如此重要，所以书本举了一些例子来加深对函数这个概念的理解，这里也把一些关键点过一下，还是有不小细节值得挖掘的：

定义域的理解：

1、举例1：

假设定义这么一个函数：

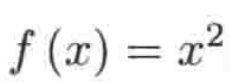
其中这个函数的定义域（函数的输入）和上域（函数的输出）都是属于 

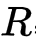
，也就是实数，啥叫实数呢，我也不知道，百度百科：

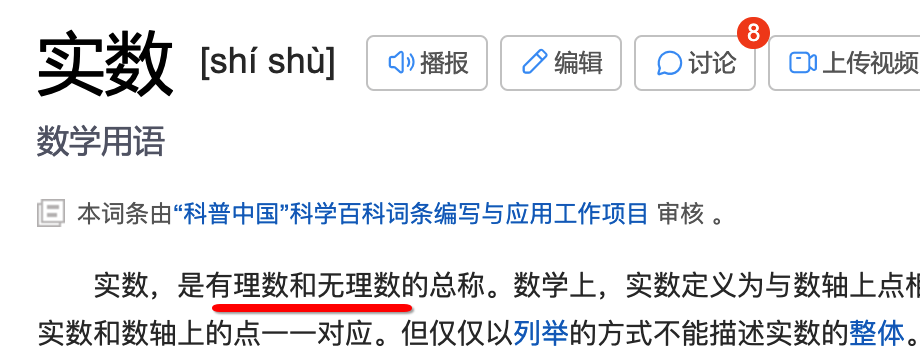
那有理数和无理数又是啥，可以自行百度，这样我们就可以将任何实数平方最终得到一个实数对吧，比如f(2) = 2 x 2 = 4、f(-1/2) = (-1/2) * (-1/2) = 1/4， 而有一个特殊的是：f(1) = 1，也就是输入和输出一样，这个其实不影响，因为函数并不要求转换后的对象一定有别于原始对象，这个小细节需要知道一下下。

另外，还有一个容易理解错的就是：f(2) = 2x2 = 4，它意味着f 将2 变成4了，其中的f是一个变换规则，而f(x)是把这个变换规则应用于变量x后得到的结果，所以说“f(x)是一个函数”是不正确的，应该说“f是一个函数”。

2、举例2：

这第二个例子其实阐述的东东比较简单，但是你需要明白这个细节，这里看一下这个函数：

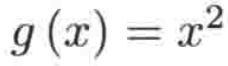
这跟上面例1的函数不是一样的式子么？是的，但是这里的定义域发生变化了，它的定义域只包含>=0的非负数，而上面例1的定义域是属于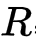实数，正因为定义域的不同，才导致对于例1中的f(x)和这里的g(x)看似一样的函数其已经产生不同了，比如x取一个负数-1/2，对于f(x)=1/4没问题，但是！！！g(x)却是没有定义的，因为该函数g的定义域必须是>=0，所以函数g会拒绝非其定义域中的一切数，这样就有一个总结了：

由于g和f有相同的规则，但g的定义域小于f的定义域，因此我们可以说g是由限制f的定义域产生的。

3、举例3：

这个例子其实还是在例2的基础上，对于函数的定义域的合法性进一步巩固，这里也来简单看一下，比较好理解：

还是例1的函数形式：

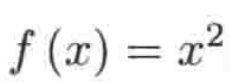
那“f(马)”是啥呢？很明显是无定义的，因为你是不能平方一匹马的对吧，但是如果定义这么一个函数其实就可以输入马了：

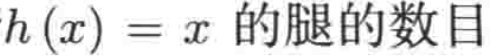
其中h的函数的定义域是所有动物的集合，所以很明显可以有：h(马) = 4，h(蚂蚁)=6，h(鲑鱼)=0，由于动物的腿不可能是负数或分数，所以很明显h函数的上域（这个概念之后就会解释到，目前简单理解就是输出值）是所有非负整数的集合。

h函数的定义域由于是所有动物的集合，所以很明显h(2)是无定义的，那h(椅子)呢？貌似h(椅子)=4呀，这里由于椅子没在定义域动物当中，所以h(椅子)也是无定义的。

4、举例4：

这个书本上举的例子就一点点恶心了，不过可以很好的说明一个问题，下面过一下：

假设你有一条狗，名字叫Junkster，它不幸患上了消化不良症，表现就是每次吃点东西嚼一会儿试图消化食物时，都会全吐出来，所以可以拟一个函数为：

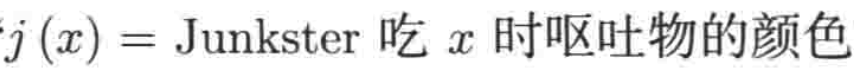
其中函数j的定义域是Junkster所吃的食物的集合，其上域是所有颜色的集合，那么就必须认为如果Junkster吃了玉米面卷，它的呕吐物始终是一种颜色（假设是红色的），这个是符合函数的定义的，但是！！！如果它的呕吐物有时候是红色的，有时候又是黄色的，那么此时就不满足函数的性质了，也就是需要记住：“一个函数必须给每一个有效的输入指定唯一的输出”。

【总结】：

 好，通过上面四个例子的学习，应该对于函数的定义域是比较清楚了，这里再来简单归纳一下核心：

1、f(x) = y，其中函数指的是f，而不是f(x)；

2、由于g和f函数有相同的规则，但是g的定义域小于f的定义域，这时我们可以说g是由限制f的定义域所产生的；

3、不在定义域的值，最终的输出是无定义的；

4、一个函数必须给每一个有效的输入指定唯一的输出；

上域、值域的理解：

接下来则来理解上述函数定义中所产生疑问的“上域”的概念了，说到上域，其实还有另一个我们耳熟能详的概念，那就是“值域”，关于这两者的区别，这里用书上的来描述一下：“值域实际上是上域的一个子集，上域是可能输出的集合，而值域则是实际输出的集合。”，是不是这定义还是有点懵，没关系，下面针对上面定义域的理解中所举例的函数一一来写出它们的值域和上域，这时你就会明白了，也是比较简单的：

1、对于

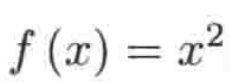
，由于定义域和上域都是实数，而根据值域的定义它是实际输出的集合，那很明显任何数的平方肯定是非负数对吧，比如，结果都等于2，所以可以看出值域确实是上域的一个子集。

2、对于

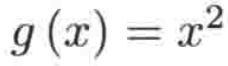
,其定义域是非负数，上域还是实数，很明显值域也是非负数的集合。

3、对于

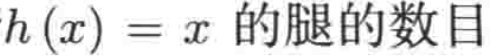
定义域是所有动物的集合，它的上域是所有非负整数的集合，而值域应该是任何动物可能会有的腿的数目的集合，通常是一个偶数，但是也有可能动物有奇数条腿，这块要列全可能你得是一个生物学家~~

4、对于

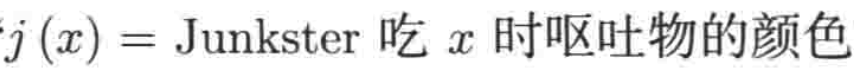
，其定义域是Junkster所吃的食物的集合，其上域是所有颜色的集合，而值域就是会包含所有可能的呕吐物的颜色。

总之，你要知道值域是上域的子集。

区间表示法：

这块就比较简单了，在我们编程时也经常能遇到，比如开区间，闭区间等， 这里看一下图就明白了：

其中我们常见的是这种表示法：

但是也要记得还有另一种表示方法：

求定义域：

有时候，函数的定义中是已经指明了定义域了，比如上面的这个函数：

但是！！！在大多数的情况下，函数的定义域是没有给出的，是需要自己来求出来的。通常定义域就是包括实数

转存失败重新上传取消集尽可能多的部分，这里举一个这样的函数：

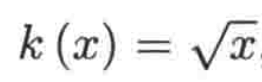
你觉得函数k的定义域是啥，全部实数么？这里的思考关键在于它：

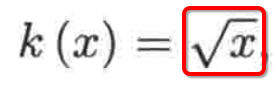
也就是得要知道平方根的规则，这块貌似是初中的知识，我想应该很多人都已经忘得差不多了，百度了一下重温下中学时光，贴一个图：

也就是这个开根号中的a必须是非负数的，看了一下百科对于算术平方根的定义也特别提到了这个条件：

那么为啥只有非负数才有算术平方根呢？其实也很好理解，因为任何实数的平方的结果都是非负数对吧，那么再对这个非负数的结果开方很明显不可能是负数的，另外这里再复习一下它跟平方根的关系，再次利用度娘：

也就是算术平方根是平方根的一种特例，好，现在我们已经对于算术平方根的规则清楚了，所以对于

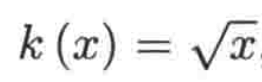
函数，很明显此时函数k的定义域为[0, ∞)，也就是>=0的所有实数的集合，这里就是通过平方根的一个规则来推出了函数的定义域了，这里其实也就道出了如何求函数定义域的一个方法了，其实还是利用你之前所知的数学规则进行推算出来的，以下几种是常见会出问题的数学规则：

• 分数的分母不能为0；【这个人人皆知】
• 不能取一个负数的平方根（或四次根、六次根，等等）；【这个刚才已经详细解释过了】
• 不能取一个负数或零的对数；
  关于这个书本上作者已经预感到大家都已经忘记这条规则了~~所以提示可以看他第9章的基础补习，嗯，很明显我是完全不知道了，移步到9章里回顾一下【数学是一门非常严谨的学科，当在学习中遇到某个知识点遗忘了，一定要花时间给补回来，不然会越学越学不懂~~借学高数的机会再重新整体一下大脑中的数学知识体系也是一个挺有价值的事~~】：
  比如这么一个方程：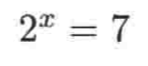

  

  
  此时就需要使用对数函数了，其结果就是：

  那如果是：

  很明显此时的x=3嘛，而这个x又可以以对数的形式来表示，所以就可以得到：，所以这里就可以用对数来表示指数的形式了，如下：

  好，接下来就是回到核心的“不能取一个负数或零的对数”的理解上来了，这里假设b是负数，看有啥问题，可能就会没有定义，比如：b=-1且x=1/2，那么==，而它已经违背上面我们已经证明的这一条了：

  所以，为了避免这样的问题产生，就需要要求b > 0，所以也一定是正的对吧，如果，那么一定会有y > 0，好核心推论点就出现了：

   很明显图中b中的幂次就不可能是一个负数或0对吧，所以你只能取一个正数的对数（b>0且y>0）。 

• tan90度是一个不存在的值；这块可能也忘了，先看一下tan的公式你就明白了：tanx=sinx/cosx，当x=90°时，即tan90°=sin90°/cos90°=1/0，分母是不能为0的，所以不存在tan90°，其实它就是上面的第一种分母为0的情况对吧，比如好理解。

综合实践：

好，接下来来一个综合求定义域的例子，如果你能把这个函数的定义域，那么这块知识点就算过关了，如下：

其实算定义域特别简单，就是套数学上哪些规则不允许，解一元一次不等式组，对于这个函数右边的式子其实就有这几个不等式：

1、根据“不能取一个负数或零的对数；”这一条规则，就有：

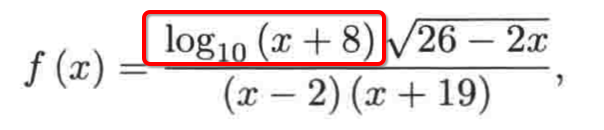
其中x+8 > 0，也就是x>-8；

2、根据“不能取一个负数的平方根”这一条规则，就有：

其中26-2x>=0，也就是x<=13；所以结合第一条的条件，此时x的取值就是(-8, 13]。

3、根据“分数的分母不能为0；” 这一条规则，就有：

(x-2)(x+19) != 0，所以就有x !=2且x!=-19， 而根据目前x的取值是(-8, 13]，x!=-19就不存在了，最终我们就找到了函数f的定义域为：除2以外的集合(-8, 13]，这种集合用一个专业表示可以为：(-8, 13] \ {2}，这里的反斜杠表示“不包括”。

利用图像求值域：

在上面，我们已经知道了函数的定义域的求解方式了，接下来则来看一下函数的值域是如何求的，书中举了两个函数：

，它的定义域为[-2, 1]，,它的定义域是所有的实数，那请问下这俩是同一个函数么？当然不是，因为定义域不一样，这个在上面已经举个类似的例子了。

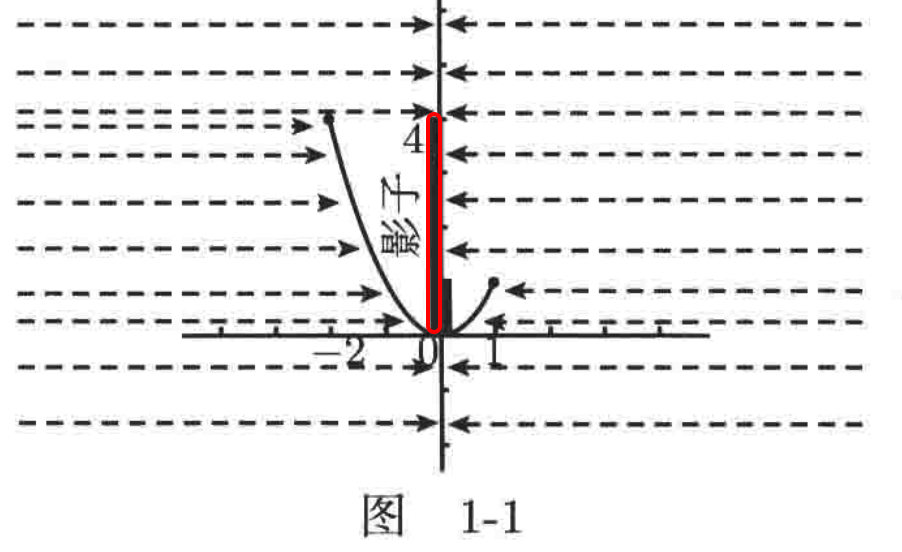
那对于F函数，你知道它的值域是多少不？既然它的定义域为[-2, 1]，我们可以将这之间的每一个实数进行平方就可以求解出F函数的值域了，很明显是[0, 4]，注意不是[-2*(-2)=4, 1 * 1 = 1]哟，利用自己心算基本也能算出来函数的值域，但是！！！这个是学习如何利用图像来求一个函数值域非常好的机会，其思想就是：画出函数的图像，然后想像从图像的左边和右边很远的地方朝向y轴水平地射入两束亮光，曲线会在y轴上有两个影子，一个在y轴的左侧，一个在y轴的右侧，而值域就是影子的并集，也就是说如果y轴上的任意一点落在左侧或右侧的影子里，那么它就处于函数的值域中，下面直观的看一下图：

当图像画出来之后，你可以看到左侧的影子覆盖了y轴从[0,4]的所有点：

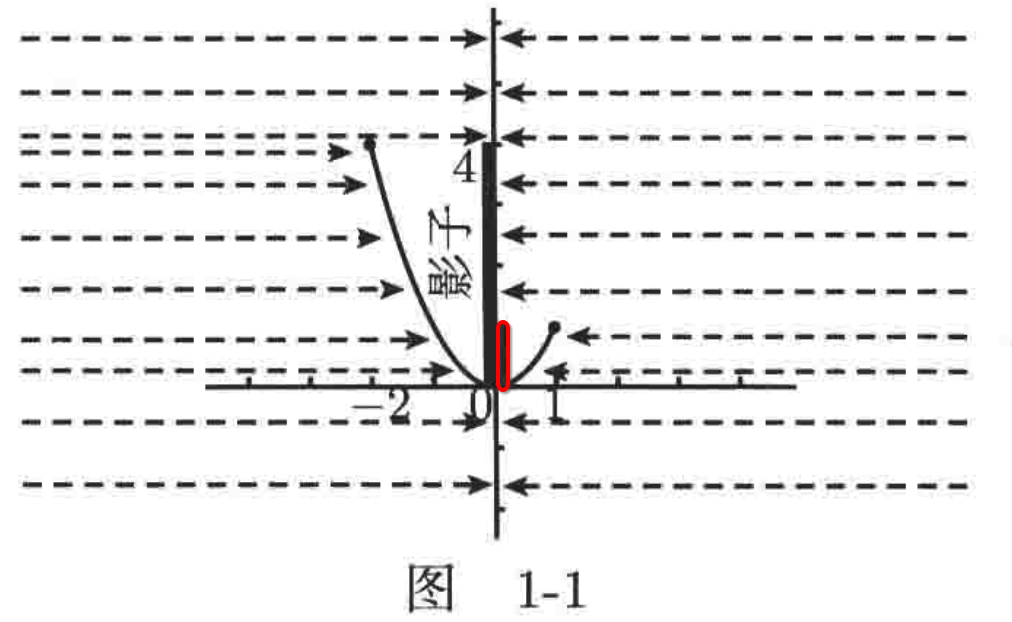
而右侧的影子覆盖了y轴从[0,1]的所有点：

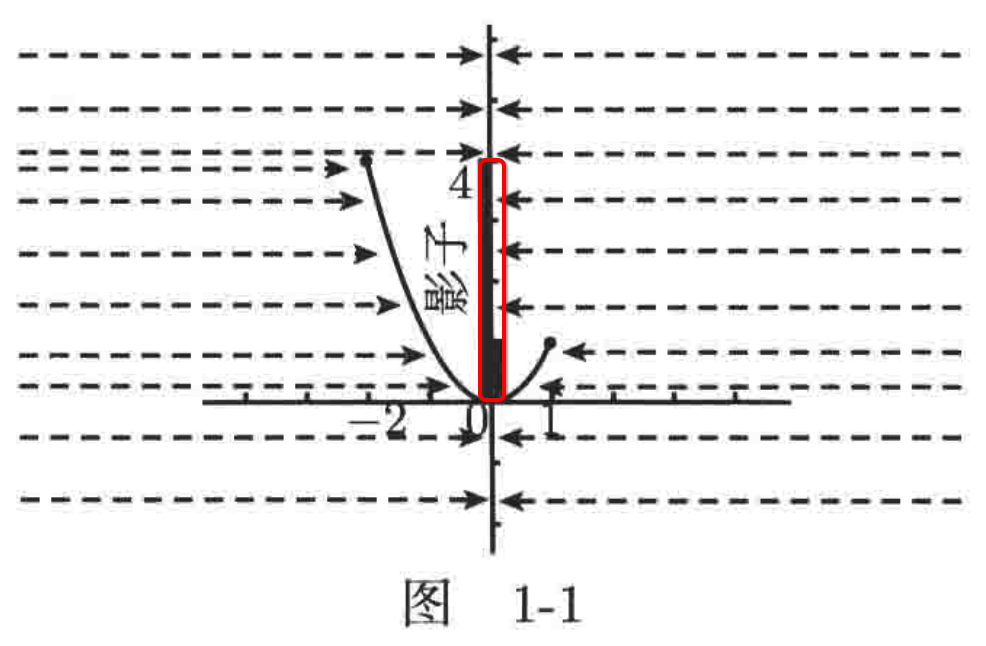
那么取两者的并集就是[0, 4]：

所以通过这种直观的函数图像也是一种求函数值域的办法，但是你或者会问，函数不可能都是这么一种呀，那其它函数的图像大脑中没有印象，用这种方式貌似要求有点高啊，其实关于函数的图像在之后的章节就会专门学到：

而且在12章中还会学习绘制函数图像的各种技巧：

所以不必担心，现在先知道函数的图像其实对于解题也是很有用的就够了。

垂线检验：

什么是函数的图像？

在上面我们也已经领略到了函数图像在解题的作用了，非常重要，因为它能让你知道函数大概长什么样子，所以这里先来认识一下函数图像的定义，这里从两个角度来概述：

角度一：函数f的图像是指它是所有坐标为(x, f(x))的点的集合，其中x在f的定义域当中；
角度二：我们以某个实数x开始，如果x在定义域当中，就可以画点(x, f(x))，当然这个点在x轴上的点x的正上方，高度为f(x)；如果x没有在定义域当中，则不能画任何点。然后对于每一个实数x，我们重复这个过程从而构造出函数的图像。

上面这概念了解一下既可，其实就是各个坐标值的连线就构成了函数的图像。

何为垂线检验？

定义：

先来看一下数学定义：“如果你有某个图像并想知道它是否是函数的图像，你就看看是否任何的垂线与图像相交多于一次。如果是多于一次则它不是函数的图像，反之则是函数的图像”。

理解：

光看这定义肯定有点懵，其实理解的关键核心在于：利用这个垂线检验的目的就是为了判断某个图像是否是函数的图像对吧，而怎么来检测呢？主要是图像中有木有两个点对应一个x坐标值，如果有，很明显这俩点的连线是垂直于这个x坐标的，而根据函数的定义：“一个函数必须给每一个有效的输入指定唯一的输出”，也就是一个输入只能对应一个唯一的输出，很明显这种情况违背了函数的定义了，那么这种情况就可以说这个图像不是函数的图像了，因为图像中存在一个输入有2个输出的情况，反之，则说明该图像就是函数的图像。

举例说明：

在了解了定义之后，下面再来借着例子来理解一下，这样就比较清晰了。

这里先来画一个“以原点为中心，半径为三个单位的图的图像”，这个比较简单，图如下：

它的函数方程应该是这样的：

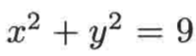
【这个是根据圆的方程公式来的：所表示的曲线是以O(0，0)为圆心，以r为半径的圆；】，那你认为这个图像是方程的图像么？不知道，所以用垂线检验的方式来检测一下，也就是在图像上画垂线，如下：

其中可以发现在-3的左边或3的右边都没有问题，垂线木有出现有两个点交于圆的情况，这个很好；而在-3和3上垂线和图像也仅仅只有一次相交，也比较好；问题就是出现在区间(-3,3)上了，垂线通过(x, 0)和圆都相交两次：

那这就不符合函数图像定义了，因为你不知道f(x)到底是对应上方的点还是下方的点对吧。

而要想让它成为函数，有两种方式：

1、把圆分成上下两个半图，只选择上一半或者下一半，由于整个圆的方程是

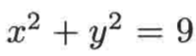
，那么上半圆的方程就为：

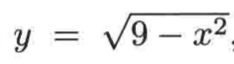
 而下半圆的方程为：

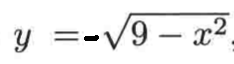
很明显这两个就是函数了，其定义域为[-3, 3]，因为用垂直检验的话，与半圆相交只有唯一的一个点。

2、还有一种方式，就是把圆的图像做一个改动，如下：

也就是只要避免一条垂线与图交于2个以上点，其图像就满足函数图像了。

反函数：

接下来学习一下反函数，这个在之后也会大量被运用到，先来理解书本上的第一句话：

假设有这么一个函数f，给一个在定义域的x输入，就能得到一个输出f(x)对吧，现在把过程返过来描述：如果你选一个实数y，那么应该赋予f函数什么样的输入才能得到这个输出y呢？

这里的关键点有两个，需要理解一下：

1、y必须在f函数的值域当中，因为它是输出嘛，而值域刚好是所有的可能输出，这个比较好理解；

2、如果y在值域当中，有可能会有很多值都满足f(x) = y，比如

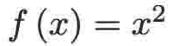
，其定义域是实数，那问一下x取何值时会输出64？很显然有两个值：8和-8；但是也有可能仅有唯一的值能满足f(x) = y，比如，同样的问题x取何值时会输出64，此时只有一个x值就是4。

定义：

好，接下来就可以给反函数来一个正式的定义了：给定一个函数f，在f的值域中选择y，在理想状况下，仅有一个x值满足f(x) = y，如果上述理想状况对于值域中的每一个y来说都成立【也就是如果x取值不唯一的话就不满足这个理想状况了】，此时就可以定义一个新的函数，它将逆转变换，从输出y出发，这个新的函数发现一个且仅有一个输入x满足f(x)=y，这个新的函数就称为f的反函数，记作

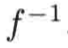
对上这个文字概念可以有一些抽象，下面以数学语言对其再总结一下：

1、从一个函数f出发，使得对于在f值域中任意y，都只有唯一的x值能满足f(x) = y，也就是说，不同的输入对应不同的输出，那么我们就可以定义它的反函数

；

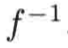
2、

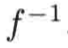
的定义域与f的值域相同；

3、

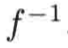
的值或和f的定义域相同；

4、

的值就是满足f(x) = y的x，所以如果f(x)=y，那么 = x；

书中最后用一个比较形像的例子对函数与反函数的关系进行了一个阐述,还挺贴切的：

变换

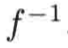
就像是f函数的撤销按钮：如果你从x出发，并通过函数f将它变换为y，那么你可以通过在y上的反函数来撤销这个变换的结果，取回x。

好，现在通过这个定义对于反函数有了一定的了解了，但是还是有如下的一些疑问会存在：

1、你如何知道只有唯一的x值满足f(x) = y 呢？

2、如果求得一个满足疑问一的函数的反函数呢？

3、反函数的图像又会是什么样了呢？

4、如果一个函数不满足疑问一的唯一性，那么有木有一些挽救的措施？

以上答案，在接下来的学习中就会一一揭晓~~

水平线检验：

对于上面提到的第一个疑问：

其最好的方法也是来看函数的图像，那怎么知道对于f函数值域中的任意一个y，只有一个x值满足f(x)=y呢？下面来挼一下思路，这个思路是引出水平线检验的一个关键：

我们想要在f函数的值域中选择一个y，并且希望只有一个x值满足f(x) = y ，那就意味着通过点(0, y)的水平线【还记得在上面我们检查函数图像是否正确用的是垂直线不？如忘了可以往上再温习一下】应该和图像只有一次相交，且交点为点(x, y)，那么此时的x就是我们想要的值；如果说水平线与函数的图像相交多于一次，是不是对于一个y，有多个x值对应？那这种情况是不符合反函数的定义的对吧，所以这种情况是比较糟糕的，但是在后续我们可以针对这种糟糕的情况限制定义域也可以让它有反函数，这个之后再说；还有另一种情况就是水平线跟函数图像压根就不相交，很明显这种代表y根据就没有在值域当中，不在反函数的讨论范围。

基于上面的思想梳理，对水平线检测就可以进行描述了：如果每一条水平线与一个函数的图像相交最多一次，那么这个函数就有一个反函数；相反如果相交有多于一次，那么这个函数就木有反函数，这里的要点是：

1、函数满足图像的定义，这里就可以用上面的垂线检验办法来检验；

2、水平线与图像相交，只有一个交点；

比如下面这两个函数的图像：

很明显图左边的函数f有一个反函数，因为没有一条水平线和y = f(x)相交大于一次对吧，而对于图右边的函数g它是没有反函数的，因为有一些水平线和y=g(x)相交于两次，这是从图像的层面来看的，而用一个角度也可以推出该函数是没有反函数的，那就是：

如果通过

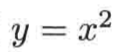
来求解x，很明显会出现两个解对吧：，这是不符合反函数的定义的。

但是，还记得在上面说过这么一句话么？

所以，对于图右侧的，如果你尝试限制一下定义域，其函数也是有反函数的：

这个情况之后再来探讨。

求反函数：

接下来再来解决上述疑问的第二个：

其实需要要写下y = f(x)，然后试着解出x既可，比如函数

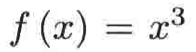
，要求它的反函数，如下：

1、写成y = f(x)的形式，也就是：

，此时就可以求出x= 

2、然后就有如下等式：

，为啥呢？这里回顾一下反函数的特性：

3、由于

中的y变量看着有点别扭，所以可以直接将它替成x，也就是为：

也就是求一个原函数的反函数，就是将它写成y=f(x)的形式，求出x，最后在原函数的右上角标一个-1，然后等于这个x既可，这块说实话有点不是很好理解，可以好好揣摩一下。 

但是！！！实际上并非所有的函数都可以轻松地求解出x来，这时则可以通过函数图像这个角度轻松的将其反函数给绘出来，基本思想就是在图像上画一条y=x的直线，然后将这条直线假想为一个双面的镜子，反函数就是原始函数的镜面反射，就比如刚才我们举例求原函数的反函数的例子，它们之间在图上的关系如下：

原函数f在y=x这面“镜子”中被反射，从而得到它的反函数了，注意：f和

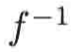
的定义域和值域都是整个实轴。这样就解决了疑问三的问题了：

限制定义域：

接下来解决疑问三的问题：

在上面举过这么一个函数的例子，它是不满足水平线检验的对吧：

也就是说函数g木有反函数，但是！！！我们可以限制函数的定义域，让其也可以有反函数，如下：

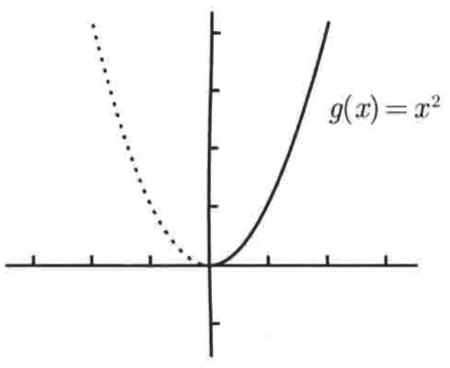
也就是将该曲线的定义域由(-∞,+∞)缩减为[0,+∞)之后，就满足水平线检验了，所以此时该函数就变成有反函数。也就是定义在定义域[0,+∞)上的函数h的反函数，其中

，下面咱们使用刚才所学的镜面反射来看一下该反函数到底长啥样？

为了找到反函数的方程，我们必须在方程

解出x，很明显此解有两个：

那我们需要哪一个解呢？根据反函数的特性：

很明显我们只需要非负数的解，即：

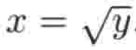
，也就是说：

此时的图像就如：

最后，咱们看一下没有通过水平线检验的定义域在(-∞,+∞)的原始函数

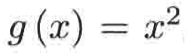
，如果在镜子y = x中进行反射，其实它会得到这么一个图像：

很明显该图是不会通过垂线检验的，也就代表它不是函数的图像，这也从另一个角度证明它是没有原函数的，此外还可以说明垂线检验和水平线检验之间的联系就是：水平线被镜子y=x反射后会变成垂线。

反函数的反函数：

这个理解起来就比较麻烦，但是呢在之后的学习中又会用到，所以，还是一点点来啃它。

如果对于一个函数f它有反函数，那么对于在f定义域中的所有x，都有这个等式成立：

，这个应该好理解，因为f(x)=y，根据反函数的这个特性就可以得出这个等式了：

同样对于在f值域当中的所有y，都有

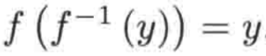
，因为f的值域和的定义域相同，所以对于f值域中的y，我们就可以取到，也就是：

对于上面这个理论理解起来可能还是有点抽象，下面举个例子再来理解一下：

比如函数

，它的反函数为：【这块如果觉得求解起来有点模糊，建议好好再温习下反函数的知识，这块未来会经常用到】，

那令x=f(x)，代入

式子中，是不是就有，也就是在上面在反函数的反函数所说有等式：

还记得在上面说过反函数就像是一个撤销按钮么？回忆一下：

也就是我们使用x作为f函数的输入，然后给出输出到

反函数上，这撤销了变换并让我们取回了x这个原始的数，这样的视角能够加深对反函数的理解。比如：最终就是求得了y对吧，所以：是f的反函数，且f是的反函数，换言之，反函数的反函数就是原始函数。

小心有限定义域的反函数的反函数：【是不是念这句话舌头会打转~~】

最后再来讨论一下这个函数的反函数的反函数：

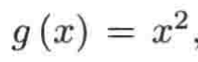
，根据之前所学，这个函数是需要限制定义域才会有反函数对吧，回忆一下：

假设我们把定义域限制在[0,+∞)，当时我们是称函数h有反函数对吧【上图中也可以看到】，也就是在限制作用域之后的函数名不用g了，而是h，但是！！！这里假设粗心，我们就把g函数看成它有反函数，看会有啥问题？我们先求得g函数的反函数为：

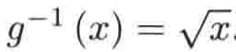
，此时再求它的反函数，你会发现它是【如果这一步看不懂，用代入法代到这个函数中你就懂了：】，也就是等于x对吧，其中x>=0。那你看出啥问题了么？是反函数的反函数应该等于原函数它呀，但是现在的结果是x，很明显是不对的，这是因为是故意看错了函数了，g是没有限制定义域的。

换另一个视角，解这个反函数的反函数：

【注意：它跟是不一样的哟】，此时会得到，是不是它也违背了“反函数的反函数是原函数”的规则？照理的呀，这里也能说明没有限制定义域的g函数是没有反函数的，由于我们粗心地将其看成g函数了，它没有限制定义域，那我x=-2，此时，所以就不成立了，不成立的根本原因在于-2没有在g的限制定义域[0,+∞)中对吧。

以上说了一大堆，其实是为了说明：我们应该使用函数h，而不是函数g，也就是对于有限制定义域的函数，我们需要改变函数的字母！！！就拿我们所用的函数例子，

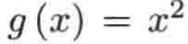
如果不限制定义域是不是没有反函数？那如果限制定义域[0,+∞)之后，就不能说g有反函数了，要给函数字母更改一下，比如更改成h，说h有反函数，这样改名是可以避免自己出错的一个手段，但是！！！实际数学家们在限制定义域时经常不会改变字母，所以把这种情形总结如下：

如果一个函数f的定义域可以被限制，使得f有反函数

，那么：

对于f值域中的所有y，都有

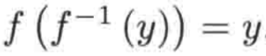
,但是！！！可能不等于x，而事实上仅当x在限制的定义域中才成立。

简单来说，对于有限制的函数，其在进行反函数的求解时，一定是要基于限制的定义域才行，不然结果就会不符合反函数的规则，记住这点就成！！！

总结：

今天先学到这，纯复习了，对于我来说其实都是全新的，小学水平，因为都不知道，然后所有的内容都是基于书本上来的，也有一些文字是直接摘抄的，但是对我而言，带着思考的抄写也是一种输出，能够加深对知识的理解，总之经过这么一篇，收获还是蛮大的，弥补了很多之前的数学基础，坚定用这种方式一步一个脚印地来把整体书给啃完，也希望用这篇让自己今年的状态回归正常，不再一直身处焦虑当中了【作为jay迷，居然还没认真去听最近周杰伦时隔6年新出的专辑的歌曲，天天就是各种忙，所以必须调整自己目前的状态，先把jay最伟大的作品好好品尝品尝~~】，加油！！！

 关注个人公众号，获得实时推送