【自校正控制】递推最小二乘法

前言

上节介绍了批处理最小二乘法，它比较适合数据的预处理，也即离线辨识，在实时性方面就不如递推最小二乘法，递推最小二乘法也就适合在线辨识

递推最小二乘法原理

递推最小二乘法的核心思想为：新的估计值 θ_hat(k) = 旧估计值 θ_hat(k - 1) + 修正项

在进行原理推导之前，我们可以先拿出批处理最小二乘法的最终公式：

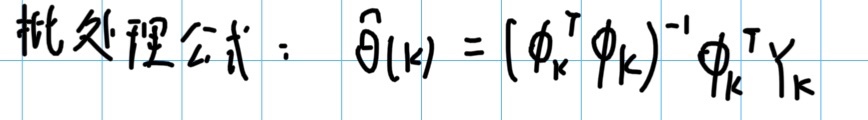
将本次数据单独提出，则数据集可以记作一个新的形式：

之后引入一个新的矩阵记作 P ：

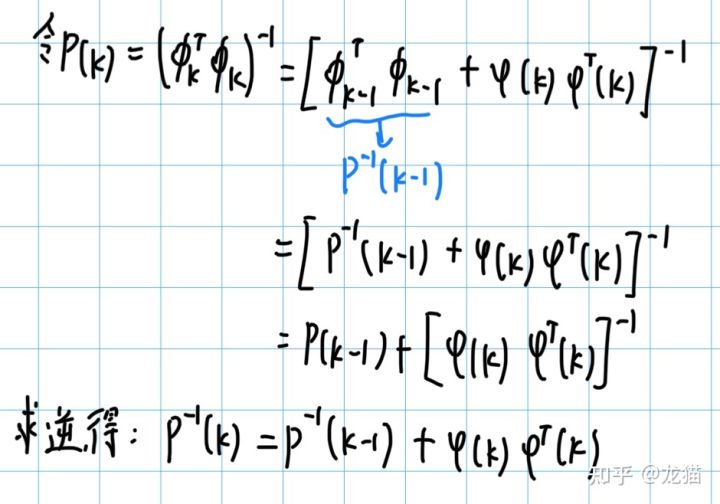
关于 P 矩阵的这几个等式都是比较重要的，后续会经常代入。

之后可以利用 P 矩阵写出上时刻的参数估计矩阵 θ_hat(k - 1) 以及 当前时刻的参数估计矩阵 θ_hat(k)：

此时，再引入一个矩阵 K = P * φ：

求解这个K的递推方程需要引入一个特殊的等式，之后就可以求解出 K 矩阵与 P矩阵的递推方程：

联立后，可以得出最终的递推方程：

实验

在原理推导结束后，可以使用matlab进行实验验证，同样的，像批处理最小二乘法中举的例子一样，假设有一个传递函数 G = b0 / (a0*s^2 + a1*s + a2)，可以将其转化为状态空间的形式：

设置一下初始的参数：

使用一个扫频信号来作为系统的输入，然后使用递推最小二乘法进行实时辨识：

需要注意的是，我们在写系统参数矩阵时，代入的为如下的参数：

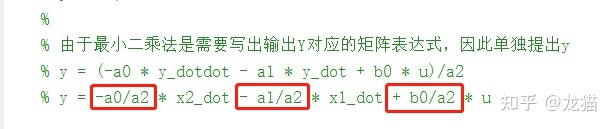
在求出估计矩阵 θ_hat(k) 后，通常我们将分母的最高次项置1，即 a0 = 1，那么其他的系数就可以求解出来了，这里我设置了一个初始系统参数值，跟原始参数还是有所区别的：

在运行程序后，得到的辨识结果为：

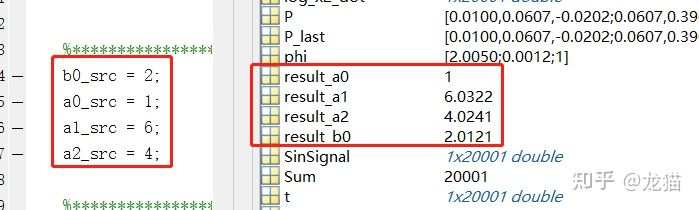
可以看到已经相差无几。