若干定义

简单路径(simple path): 其上的所有顶点都是互异的，但第一个顶点和最后一个顶点可能相同。
如果在一个无向图中从每一个顶点到每个其他顶点都存在一条路径，则称该无向图是连通的(connnected)。具有这样性质的有向图称为是强连通的；如果一个有向图不是强连通的，但是它的基础图(即其弧上去掉方向所形成的图)是连通的，那么该有向图称为是弱联通的；完全图是其每一对顶点间都存在的一条边的图。

图的表示

表示图的一种简单的方法是使用一个二维数组，称为邻接矩阵(adjacent matrix)表示法。对于每条边 (u, v)，我们置 A[u][v] 为 true；否则，数组的对应元素就是 false。如果边有一个权，那么我们可以置 A[u][v] 等于该权，而使用一个很大或者很小的权作为标记表示不存在的边。虽然这种表示的优点是非常简单，但它的空间需求为 O(|V|²)，如果图的边不是很多，那么这种表示法的代价就太大了。如果图是稠密的：|E|=O(|V|²)，则邻接矩阵就是一种合适的表示方法。

如果图是稀疏的，则更好的解决方法是使用邻接表(adjacency list)表示。对每一个顶点，我们使用一个表存放所有邻接的顶点。此时空间需求为 O(|E|+|V|)，它相对于图的大小而言是线性的。

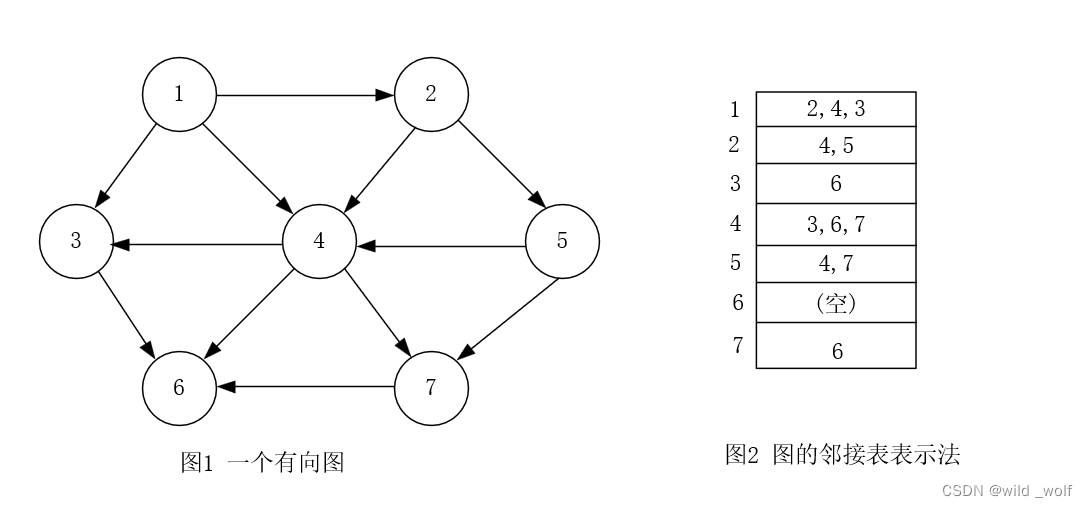
邻接表是表示图的标准方法。无向图可以类似地表示。每条边(u, v) 出现在两个表中，因此空间的使用基本上是双倍的。在图论算法中通常需要找出与某个给定顶点 v 邻接的所有的顶点。而这可以通过简单地扫描相应的邻接表来完成，所用时间与这些找到的顶点的个数成正比。

对任一顶点，重要的关键在于能够迅速得到与该顶点邻接的那些顶点的表，所以两个基本的选择是，或者使用一个映射，在这个映射下，关键字是顶点而其值就是相应的邻接表，或者把每一个邻接表作为 Vertex 类的数据成员保存起来。

拓补排序

拓补排序(topological sort) 是对有向无圈图的顶点的一种排序，使得如果存在一条从 v_i 到 v_j 的路径，那么在排序中 v_j 就在 v_i 的之后出现。

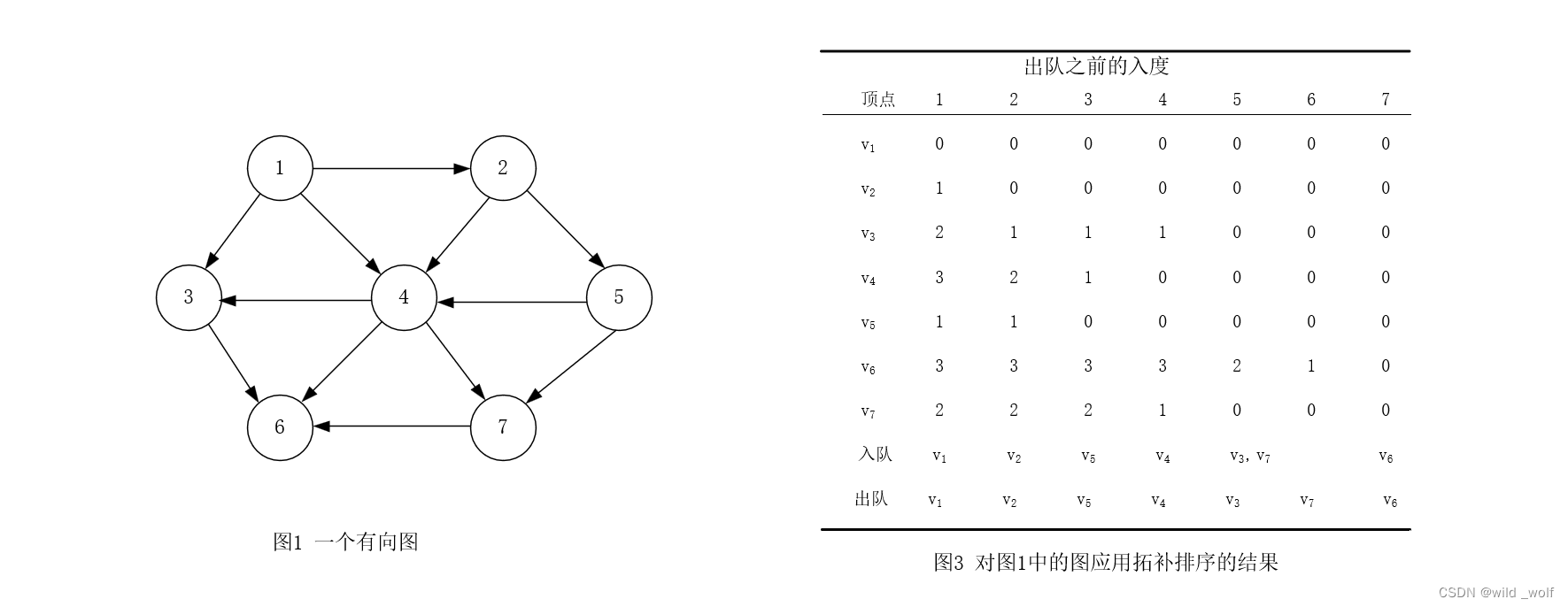
一个简单的求拓补排序的算法是先找出任意一个没有入边(incoming edge) 的顶点。然后我们显示出该顶点，并将它和它的边一起从图中删除，然后对图的其余部分继续应用这样的方法来处理。在图1 中， v₁, v₂, v₅, v₄, v₃, v₇, v₆ 和 v₁, v₂, v₅, v₄, v₇, v₃, v₆ 两个都是拓补排序。

为将上述方法形式化，我们把顶点 v 的入度(indegree) 定义为边 (u, v) 的条数。可使用一个栈或一个队列来实现这个过程。这个示例选择队列来实现。首先，对每个顶点计算它的入度。然后，将所有入度为0 的的顶点放入一个初始为空的队列中。当队列不空时，删除一个顶点 v，并将邻接到 v 的所有顶点的入度均减少1。只要一个顶点的入度降为0，就把该顶点放入队列中。此时，拓补排序就是顶点出队的顺序。 如图3所示。

拓补排序代码

/**
* 使用队列实施拓扑排序的伪代码
*/
void Graph::topsort()
{
	Queue<Vertex> q;
	int counter = 0;

	q.makeEmpty();
	for each Vertex v
		if (v.indegree == 0)
			q.enqueue(v);

	while (!q.isEmpty())
	{
		Vertex v = q.dequeue();
		v.topNum = ++counter;  //分配下一个拓扑编号

		for each Vertex w adjacent to v
			if (--w.indegree == 0)
				q.enqueue(w);
	}

	if (counter != NUM_VERTICES)
		throw CycleFoundException{ };
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26