本文是接着上一篇深度学习之 8 深度模型优化与正则化_水w的博客-CSDN博客

目录

4.参数初始化与数据预处理

初始化方法：

（1）基于固定方差的参数初始化

（2）基于方差缩放的参数初始化

（3）Xavier初始化

（4）He初始化：与前一层的神经元个数有关

（5）对比：

数据预处理

（1）数据归一化

逐层归一化

（1）批量归一化：对一个中间层的单个神经元进行归一化操作

（2）层归一化：对一个中间层的所有神经元进行归一化

（3）批量归一化 vs 层归一化

超参数优化

（1）网格搜索

（2）随机搜索

（3）贝叶斯优化 

（4）动态资源分配

过拟合与正则化

（1）ℓ1和ℓ2正则化

（2）提前停止 

（3）Dropout（丢弃法）

（4）数据增强 

---

4.参数初始化与数据预处理

梯度下降法需要在开始训练时给每一个参数赋一个初始值

➢ 初始化为0：对称权重现象；

➢ 初始化范围太小：导致信号慢慢消失，还会使得Sigmoid型激活函数丢失非线性能力；

➢ 初始化范围太大：导致信号变得过大，还会使得Sigmoid型激活函数变得饱和，从而导致梯度消失；

初始化方法：

➢ 预训练初始化：Pre-Training → Fine-Tuning

➢ 固定值初始化：对于一些特殊的参数，我们可以根据经验用一个特殊的固定值来进行初始化，如偏置（bias）通常用0初始化

➢ 随机初始化方法：

• 基于固定方差的参数初始化
• 基于方差缩放的参数初始化
• 正交初始化方法

（1）基于固定方差的参数初始化

（2）基于方差缩放的参数初始化

➢ 一般而言，参数初始化的区间应该根据神经元的性质进行差异化的设置；

        ⚫ 如果一个神经元的输入连接很多，它的每个输入连接上的权重就应该小一些以避免神经元的输出过大或过饱和；

➢ 初始化一个深度网络时，为了缓解梯度消失或者爆炸问题，须尽可能保持每个神经元的输入和输出的期望始终为0，方差保持一致；

        ⚫ 根据神经元的连接数量自适应地调整初始化分布的方差；

        ⚫ 方差缩放

（3）Xavier初始化

  

（4）He初始化：与前一层的神经元个数有关

（5）对比：

• Xavier 初始化和 He 初始化的具体设置情况

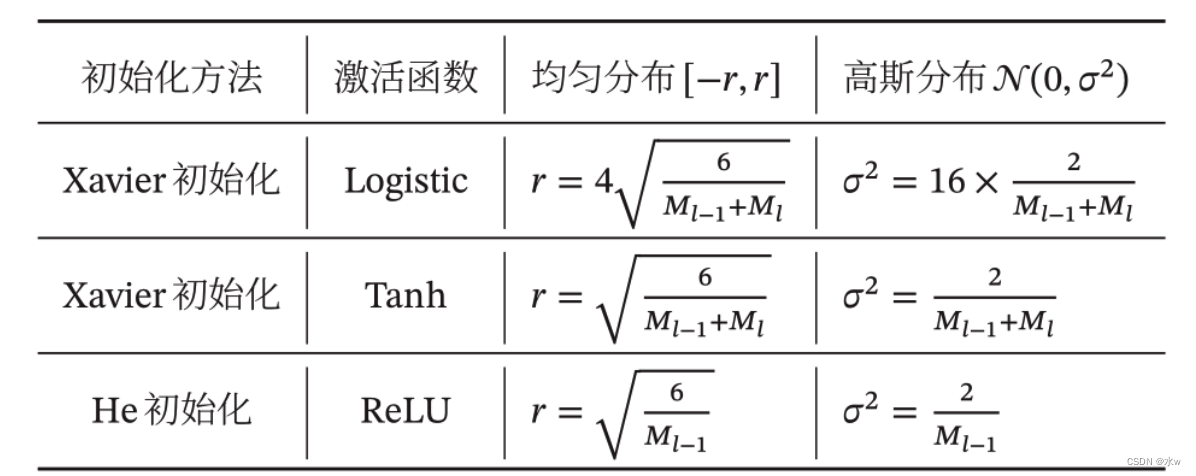
➢正交初始化

        • 用均值为 0 、方差为 1 的高斯分布初始化一个矩阵；

        • 将这个矩阵用奇异值分解得到两个正交矩阵，并使用其中之一作为权重矩阵。

数据预处理

➢ 数据尺度(Scale)不一样对优化的影响

        图1：x1数值太小了，因此参数w1就要大一些，才能达到和x2产生的w2一样的效果，导致需要经过很多次迭代才能找到最优点。

        图3：x1和x2尺度一致，画出来就比较均衡。

为了达到图2这样效果，我们需要进行数据归一化。

（1）数据归一化

➢ 简单缩放（如：最小最大值归一化 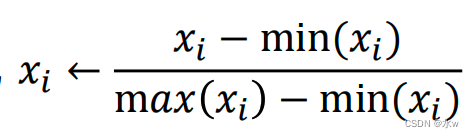；图像像素值除以 255） 

➢ 逐样本均值消减(也称为移除直流分量)：若数据是平稳的（即数据每一个维度的统计都服从相同分布），那么可以考虑在每个样本上减去数据的统计平均值。

➢ 特征标准化：使得数据的每一个维度具有零均值和单位方差。

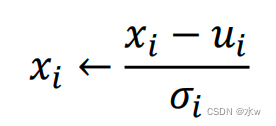
白化 —要消除各个维度之间的相关性。除了中心要在0之外，要保证各个维度是相同的（归一化没有这个要求）

— 降低输入的冗余性，降低特征之间的相关性,使得所有的特征具有相同的方差. 

        ➢ PCA白化：先PCA进行基转换，降低数据的相关性，再对每个输入特征进行缩放(除

以各自的特征值的开方)，以获得单位方差，此时的协方差矩阵为单位矩阵。

        ➢ ZCA白化：ZCA白化只是在PCA白化的基础上做了一个逆映射操作，使数据转换到原

始基下，使得白化之后的数据更加的接近原始数据。

实际建议：

        ➢ 自然灰度图像：均值消减 → PCA/ZCA白化

        ➢ 彩色图像：简单缩放 → PCA/ZCA白化

        ➢ 音频 (MFCC/频谱图)：特征标准化 → PCA/ZCA 白化

        ➢ MNIST 手写数字：简单缩放/逐样本均值消减（→ PCA/ZCA 白化）

输入的数据归一化了，中间输出数据怎么办？------>逐层归一化

逐层归一化

目的：

        ➢ 解决内部协变量偏移问题（每一层输入的分布不一样）；

        ➢ 解决梯度消失、梯度爆炸；

        ➢ 获得更平滑的优化地形；

归一化方法：

        ➢ 批量归一化（Batch Normalization，BN） 

        ➢ 层归一化（Layer Normalization） 

        ➢ 权重归一化（Weight Normalization）

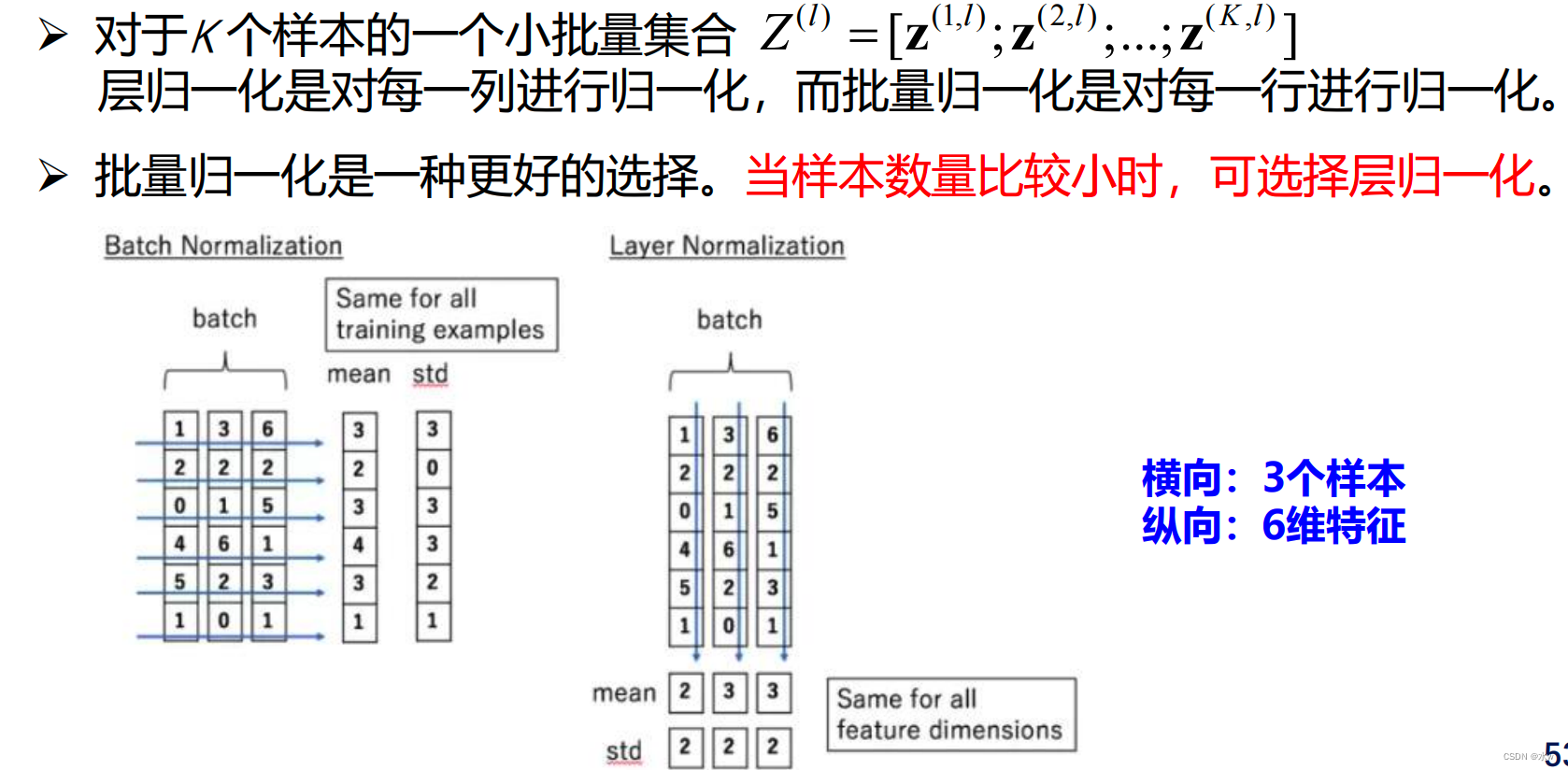
（1）批量归一化：对一个中间层的单个神经元进行归一化操作

（2）层归一化：对一个中间层的所有神经元进行归一化

（3）批量归一化 vs 层归一化

超参数优化

◼ 神经网络中的超参数：

        ➢ 层数、每层神经元个数、激活函数、学习率（各优化算法中包含的参数）、正则化系数、mini-batch 大小

◼ 优化难点：

        ➢ 超参数优化是一个组合优化问题：无法像用GD来优化

        ➢ 评估一组超参数配置的时间代价非常高

◼ 优化方法：

➢ 网格搜索、随机搜索、贝叶斯优化、动态资源分配、神经架构搜索

（1）网格搜索

网格搜索（Grid Search）是一种通过尝试所有超参数的组合来寻址合适一组超参数配置的方法。

假设总共有K 个超参数，第k 个超参数的可以取𝑚𝑘个值。比如学习率α，可以设置：α ∈ {0.01,0.1,0.5,1.0}.这些超参数可以有 𝑚1 × 𝑚2 ×···× 𝑚𝐾 个取值组合。网格搜索根据这些超参数的不同组合分别训练一个模型，然后测试这些模型在验证集上的性能，选取一组性能最好的配置。

效率低下

  

（2）随机搜索

超参数对模型性能影响程度不一样。采用网格搜索会在不重要的超参数上进行不必要的尝试。一种改进方法是对超参数进行随机组合，然后选取一个性能最好的配置，这就是随机搜索。

（3）贝叶斯优化 

贝叶斯优化是一种自适应的超参数优化方法，根据当前已经试验的超参数组合，来预测下一个可能带来最大收益的组合．

        ➢ 假设超参数优化的函数𝑓(𝑥)服从高斯过程，则𝑝(𝑓(𝑥)|𝑥)为一个正态分布

        ➢ 贝叶斯优化过程是根据已有的𝑁组试验结果𝐻 = 𝑥𝑛, 𝑦𝑛 𝑛𝑁=1 𝑦𝑛为𝑓 𝑥𝑛 的观测值来建模高斯过程，并计算𝑓 𝑥 的后验分布 𝑝𝐺𝑃(𝑓(𝑥)|𝑥, 𝐻) 

        ➢ 需用尽可能少的样本使得后验分布接近真实分布，定义一个收益函数a 𝑥, 𝐻 

        ➢ 收益函数来判断一个样本是否能够给建模后验概率提供更多的收益，收益函数的定义有很多种方式，一个常用的是期望改善。

（4）动态资源分配

超参数优化中，每组超参数配置的评估代价比较高。如果可以在较早的阶段就能够估计出一组配置的效果会比较差，那么就可以中止这组配置的评估，将更多的资源留给其它配置。

过拟合与正则化

如何提高神经网络的泛化能力：

        ➢ ℓ1和ℓ2正则化

        ➢ 提前停止

        ➢ Dropout

        ➢ 数据增强

（1）ℓ1和ℓ2正则化

ℓ1和ℓ2正则化是最常用的正则化方法，通过约束参数的 ℓ1和ℓ2范数来减小模型在训练数据集上的过拟合现象。

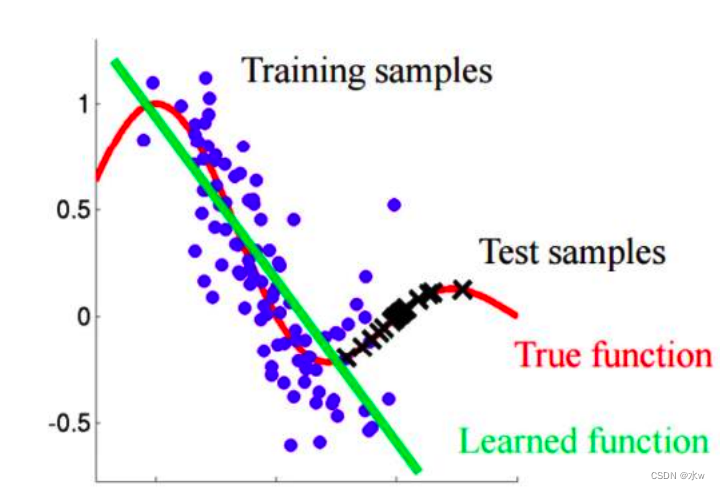
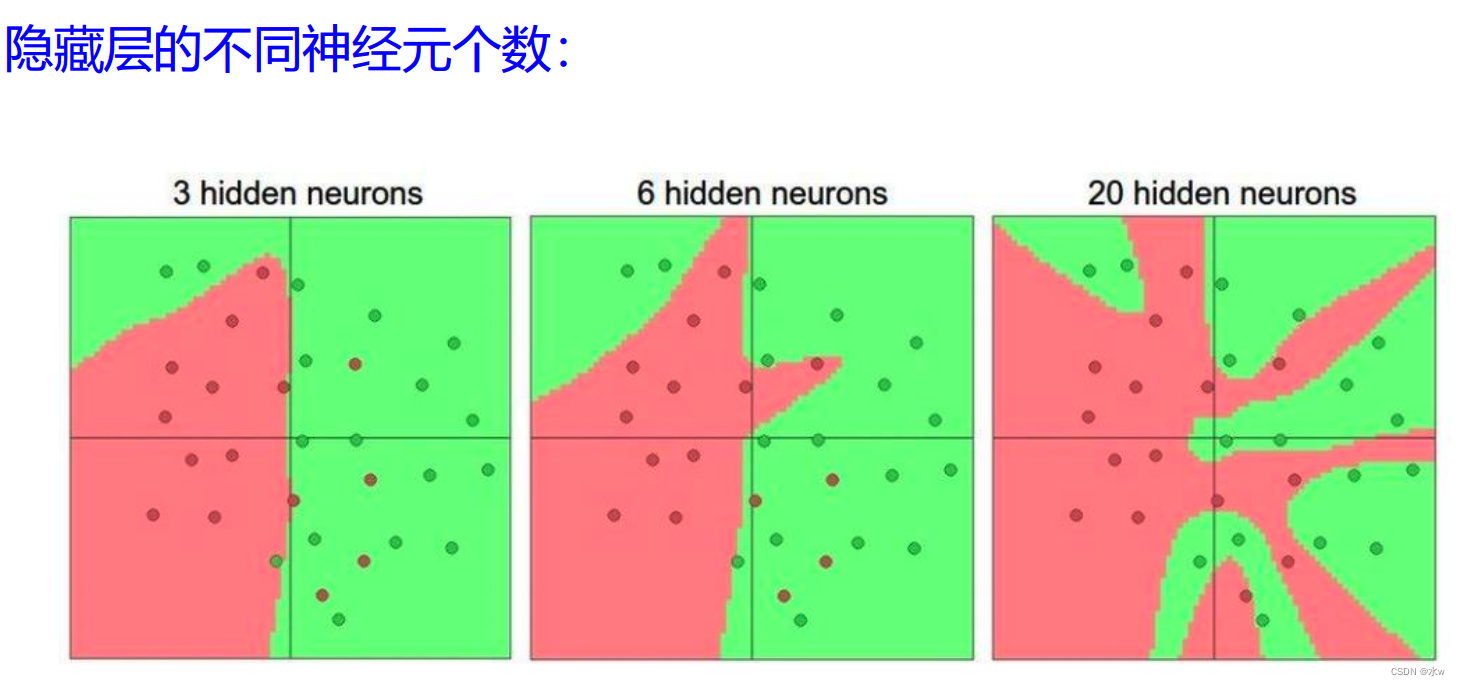
◼ 我们可以看到下图中，同样是30个样本，学习的效果就是不一样。 

• 3个神经元：它的表达能力一般，相当于一个判别函数
• 6个神经元：
• 20个神经元：模型的表单了已经很强了，基本拟合的很好了，没有分错的样本，基本都分开了。但是这不是我们想要的，有些过拟合了。

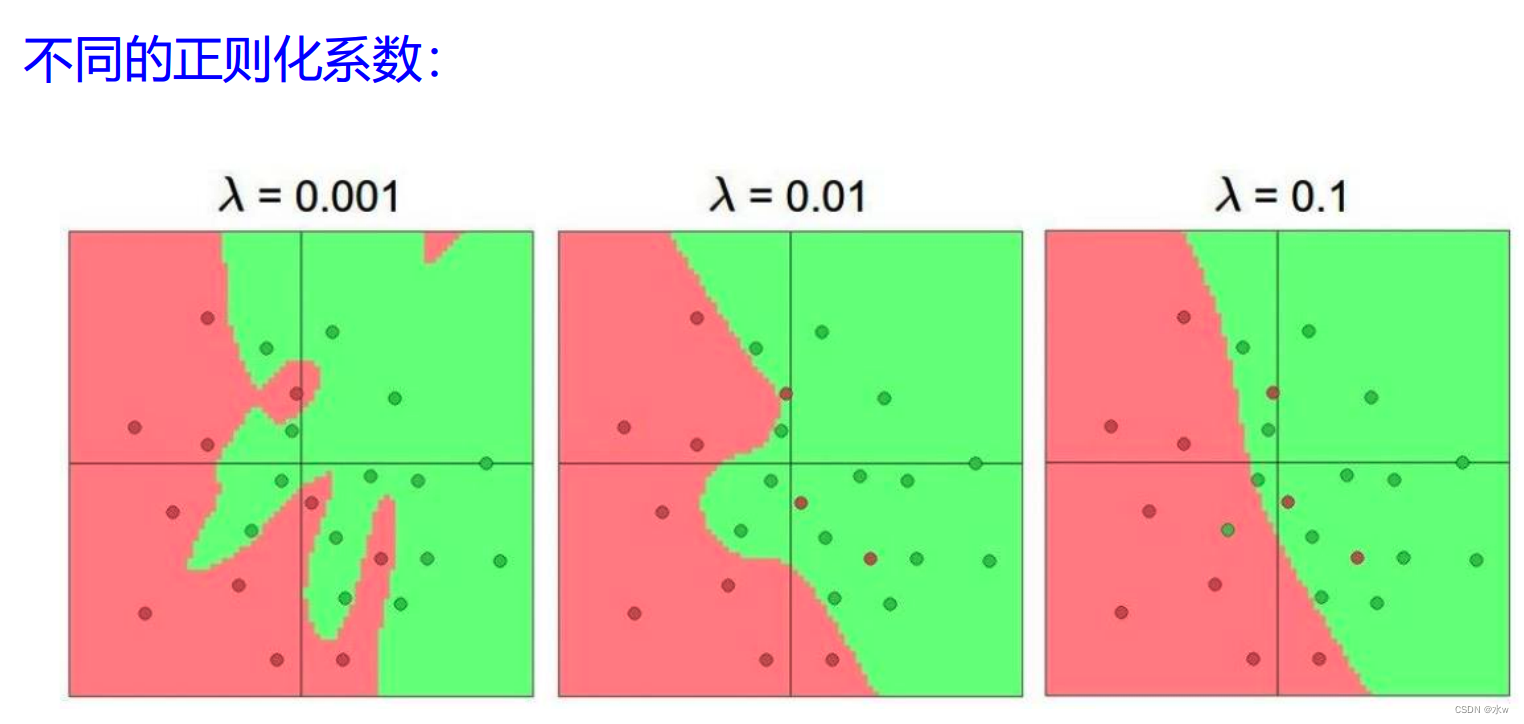
◼ 那怎么办？我们使用正则化，

• 0.1时，对参数的约束简单，导致形成的判别决策的分界线很顺滑。既符合数据的分布，也不会太复杂。 

（2）提前停止 （早停）：纯粹的物理方法

随着迭代次数的增加，在训练集上发现损失越来越低。但是在验证集上，发现开始慢慢往上走，这就意味着此时训练集拟合的太好了，有些过拟合了，而失去了一般性。​​​​​​​

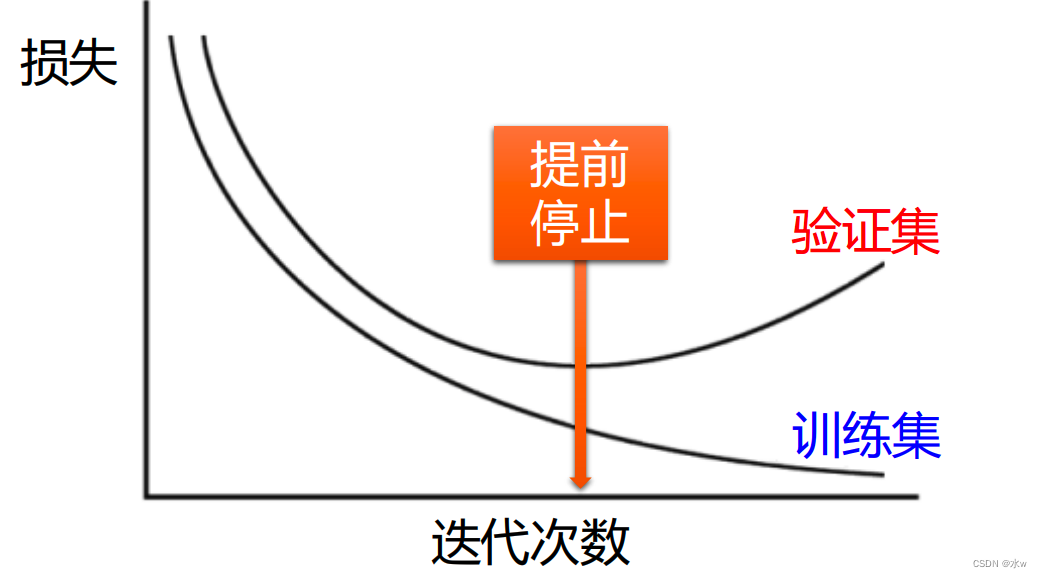
 提前停止 （早停）：使用一个验证集来测试每一次迭代的参数在验证集上是否最优。如果在验证集上的错误率不再下降，就停止迭代。

（3）Dropout（丢弃法）

我的神经网络很复杂，它的表达能力很强。但是我想要把它变得简单一些，那么我就想要扔掉一些神经元。 扔掉之后，神经网络的表达能力就没那么强了，也就没那么容易过拟合了。

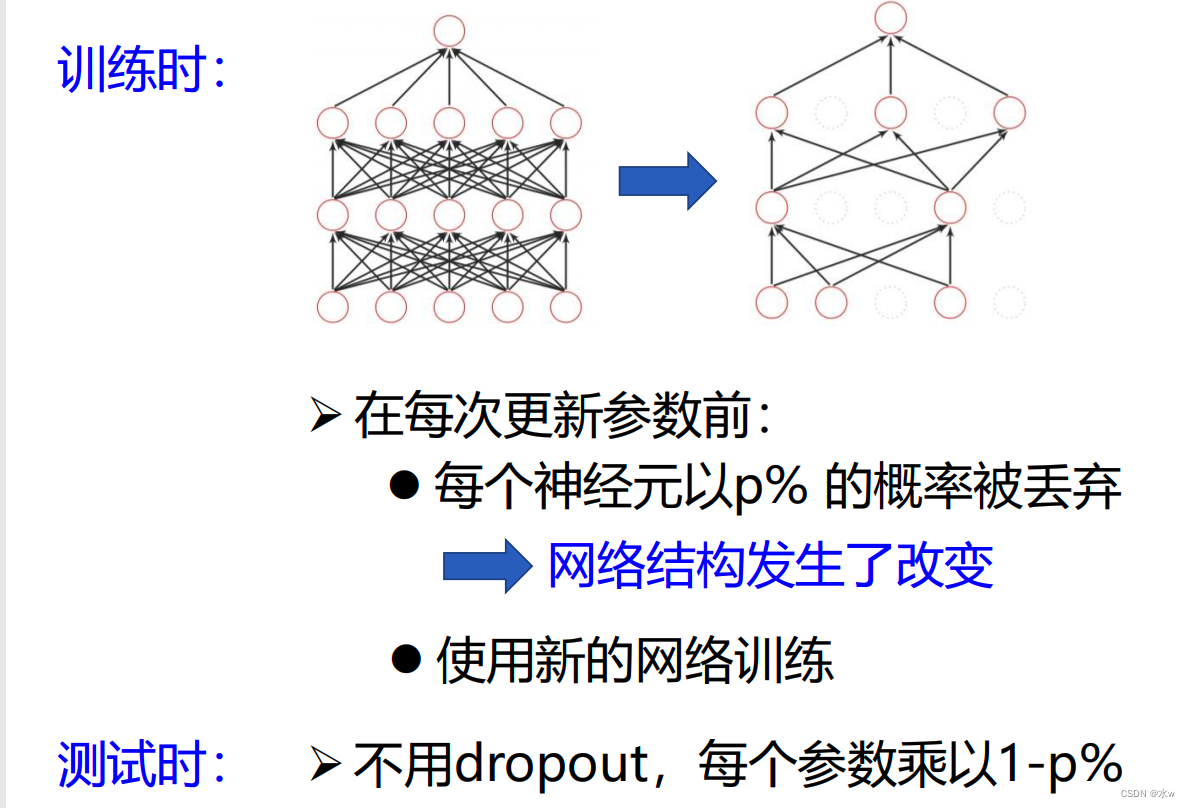
Dropout为什么会提升网络优化效果？

        ➢ Dropout简化了网络，参数量减少，表达能力下降，防止过拟合

        ➢ Dropout可看作是一种集成学习

（4）数据增强 

图像数据的增强主要是通过算法对图像进行转变，引入噪声等方法来增加数据的多样性以及训练数据量。

图像数据的增强方法：

        ➢ 旋转（Rotation）：将图像按顺时针或逆时针方向随机旋转一定角度；

        ➢ 翻转（Flip）：将图像沿水平或垂直方法随机翻转一定角度；

        ➢ 缩放（Zoom In/Out）：将图像放大或缩小一定比例；

        ➢ 平移（Shift）：将图像沿水平或垂直方法平移一定步长；

        ➢ 加噪声（Noise）：加入随机噪声。