什么是评价类问题？
题干中要求你确定评价指标，形成评价体系。
常见的评价类算法有？
层次分析法、TOPSIS法、熵权法、变异系数法、主成分分析法等等。

一、原理

简称AHP，是指将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。

二、要点

需要利用打分法设置评价指标，这个打分可以依赖于常识、文献、专家建议等。

打分的分数为1-9十个整数，利用1-9表示重要程度，列表格两两比较。

三、举例及代码

1. 举例

2. 分析

3. 解题思路

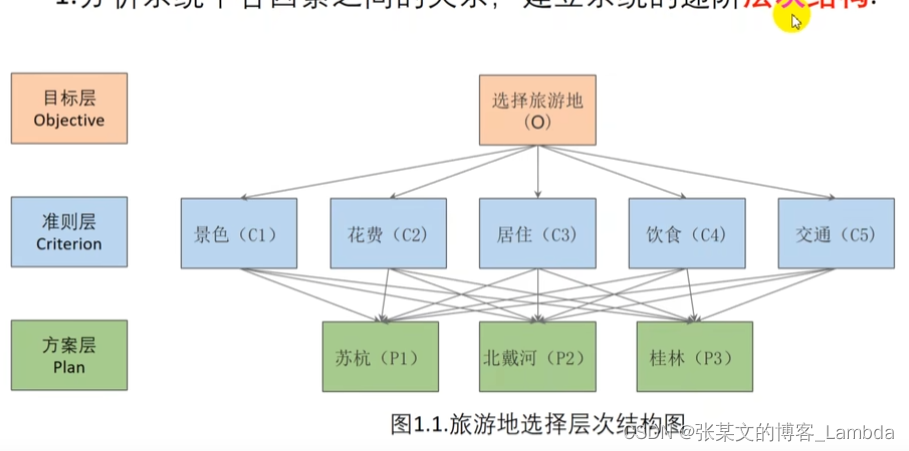
（1）建立层次结构

注意：评价的决策层不能太多，太多的话n会很大，判断矩阵和一致矩阵差异可能会很大。

（2）利用打分法打分

（3）形成判断矩阵

假设现对小明进行提问（实际过程中，由专家/文献/实际情况支撑打分环节的分数），就这样小明回答了10次[组合数C(5,2)]，根据他所回答的填好了上面这张表。

具体展示了剩余4张表格的数据，形成总共5个判断矩阵（5个指标对应5个判断矩阵）：

观察可以发现，有矛盾之处，也就是下面需要处理的不一致现象。

（3）转换一致矩阵

为了解决上述问题，提出了一致矩阵。
例如：a苏杭桂林=a苏杭北戴河a北戴河桂林=22=4
一致矩阵的特点是：一致矩阵满足各行(各列)之间成倍数关系。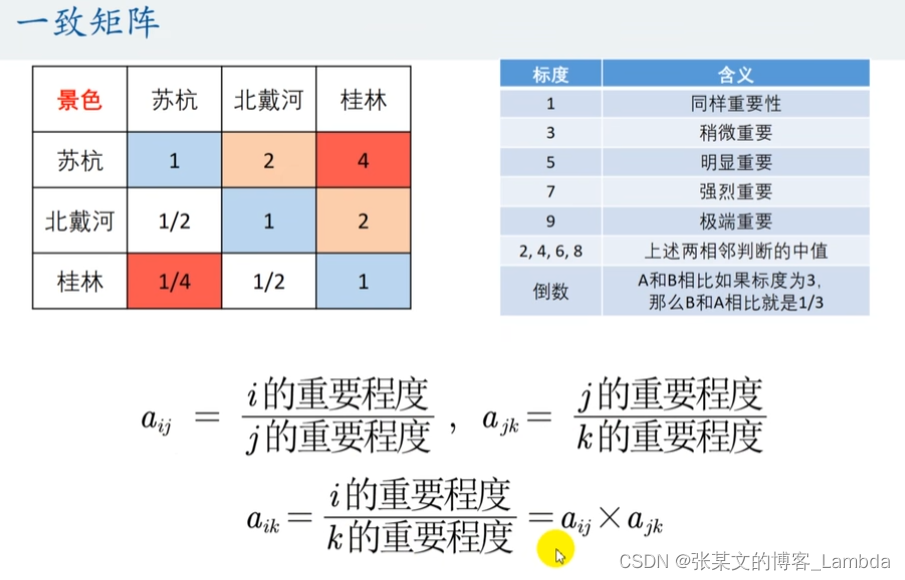

（4）进行一致性检验

我们在使用判断矩阵求权重之前，必须对其进行一致性检验。

4. 具体步骤

（1）打分列表格
（2）计算一致矩阵的权重结果

（3）计算判断矩阵的权重

- ①算术平均法求权重

首先展示了算术平均法在论文中需要列出的数学公式，如下图：

结合上面的所举例的例题，有如下计算过程：
- ②几何平均法求权重

展示了几何平均法中需要的公式，如图。并且对比了算术平均法和几何平均法计算结果的不同，如图中表所示：

• ③特征值法求权重
  推荐使用该方法。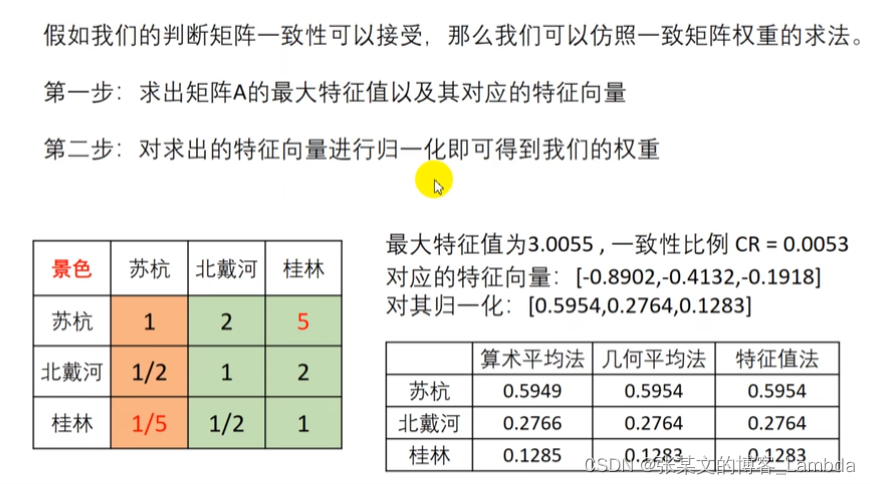
  （4）计算各个方案的得分
  根据计算的方案得分，分数越高越推荐。
  

四、代码

import numpy as np
from functools import reduce
'''1.输入数据'''
print("请输入判断矩阵大小：")
n = eval(input())
print("请输入判断矩阵：")
A = np.ones((n, n))
for i in range(n):
    A[i] = input().split(" ")
    A[i] = list(map(float, A[i]))
print("输入判断矩阵为：\n{}".format(A))

'''2.一致性检验'''
# 求解特征向量的最大特征值
w, v = np.linalg.eig(A)
wIndex = np.argmax(w)
wMax = np.real(w[wIndex])
print("最大特征值数值：{}".format(wMax))
# 输出一致性指标CI
CI = (wMax - n)/(n-1)
print("CI数值：{}".format(CI))
# 输出平均随机一致性指标RI, 直接查表可得, 不同标准数值有所差别。
# RI数据来源：洪志国.层次分析法中高阶平均随机一致性指标(RI)的计算[J].计算机工程与应用,2002(12):45-47+150.
RI = [0, 0, 0.0001, 0.52, 0.89, 1.12, 1.26, 1.36,
      1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58, 1.59,
      1.5943, 1.6064, 1.6133, 1.6207, 1.6292]
print("RI数值：{}".format(RI[n]))
# 输出一致性比例CR
CR = CI/RI[n]
print("CR数值：{}".format(CR))

# 判断是否可以接受
if CR > 0.1:
    print("该判断矩阵A的一致性不可以接受.")
else:
    print("该判断矩阵A的一致性可以接受.")

    '''3.归一化处理'''
    lineSum = [sum(m) for m in zip(*A)]
    D = np.zeros((n, n))
    for i in range(n):
        for j in range(n):
            D[i][j] = A[i][j]/lineSum[j]
    print("归一化判断矩阵为：\n{}".format(D))

    '''4.计算权重'''
    # 算术平均法计算权重
    ans = np.zeros(n)
    for i in range(n):
        ans[i] = np.average(D[i])
    print("算术平均法权重计算结果为：\n{}".format(ans))
    # 几何平均法计算权重
    ans = np.zeros(n)
    for i in range(n):
        ans[i] = reduce(lambda x,y:x*y, A[i])
        ans[i] = pow(ans[i], 1/n)
    ans = [e/np.sum(ans) for e in ans]
    print("几何平均法权重计算结果为：\n{}".format(ans))
    # 特征值法计算权重
    ans = np.zeros(n)
    vIndex = np.argmax(v)  # 对应最大特征值的特征向量索引
    vMax = np.real(v[:, vIndex])
    ans = [e/np.sum(vMax) for e in vMax]
    print("特征值法权重计算结果为：\n{}".format(ans))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

实验结果如图所示：

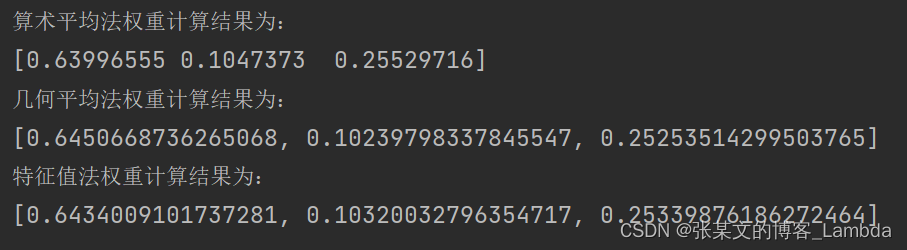
五、参考链接

1.视频资源来源B站–清风
2.CSDN博客笔记