拉格朗日乘子法与罚函数

在了解增广拉格朗日乘子法之前，先了解一下拉格朗日乘子法和罚函数。

拉格朗日乘子法

基本的拉格朗日乘子法(又称为拉格朗日乘数法)，就是求函数f(x1,x2,...)在约束条件下极值的方法。其主要思想是引入一个新的参数λ(即拉格朗日乘子)，将约束条件函数与原函数联系到一起，使能配成与变量数量相等的等式方程，从而求出得到原函数极值的各个变量的解。

假设目标函数为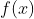，约束条件为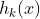

其中l表示有l个约束条件。

在这里我们举一个例子进行理解。

假设有一个方程为的椭球，我们要求这个椭球内接长方体的最大体积。

那么也就是说我们要在的条件下，求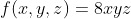的最大值。

现在我们定义一个拉格朗日函数：

其中是各个约束条件的待定系数。

接下来求偏导为0的解如：

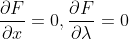
回到我们的题目，就可以将问题转化为：

其中使用

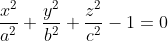
是因为我们的约束条件中要求的格式是

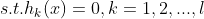
接下来对求偏导可得：

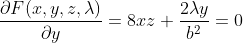
联立前三个方程并代入第四个方程后可以求解为：

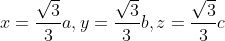
最后可得

罚函数

罚函数法是一种广泛采用的约束优化方法，用于解决约束条件下的最优化问题。

考虑我们的问题为：

将原约束优化问题转变为无约束优化问题：

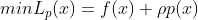
其中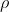表示惩罚参数。对于等式约束，可以定义罚函数：

如果满足约束条件则无影响，但是如果没有满足约束条件，则会施加惩罚。

下一篇文章继续了解对偶上升法和增广拉格朗日乘子法