【信息检索】信息检索系统实现

实验内容与任务

数据爬虫

在这里插入图片描述

倒排索引的构建

布尔模型倒排索引构建

在这里插入图片描述

布尔运算实现

在这里插入图片描述

权值计算

在这里插入图片描述

权值排序

在这里插入图片描述

支持bool查询及四种模型的自然语言检索

在这里插入图片描述

RSV计算

在这里插入图片描述

一元混合语言模型MLE和二元混合语言模型MLE

在这里插入图片描述

实验过程与数据分析

系统架构

在这里插入图片描述

配置文件

在配置文件当中，可以配置许多系统参数。如各种权限参数，日志参数以及路径参数。

class Config:
    def __init__(self) -> None:
        self.logFileName = "./tmp/log.log"
        self.logLevel = logging.DEBUG
        self.logEncoding = "utf8"
        self.datasetPath = "../dataset/"
        self.contentWeight = 0.4
        self.titleWeight = 0.6
        self.lambdaWeight = 0.5
1
2
3
4
5
6
7
8
9

数据爬虫实现

在该系统中，使用requests包进行http请求，使用bs4解析获取的html文件，生成对应的Ci对象。同时将生成的词对象以JSON文件格式保存在dataset当中，dataset的位置可以在Config中进行配置。

倒排索引构建

本小节将介绍全文倒排索引的构建、标题倒排索引的构建。语言模型WordMap的构建，以及分词算法。

分词算法

本系统使用中文自然语言分词库：jieba进行分词，在分词之前，先去除词当中的各种符号及空格，然后进行自然语言分词，并记录每个分词的位置信息，和频率，储存在Term中。

    def cut(self, text: str, ci: Ci, mode: str = "default") -> Dict[str, Term]:
        trimText = text.translate(
            str.maketrans("", "", "；！—，。()？《》、（）：“”\\·\n"))
        segList = list(jieba.tokenize(trimText, mode))
        ret = {}
        for word, start, stop in segList:
            if word not in ret:
                term = Term()
                term.docId = ci.id
                term.freq = 1
                term.pos = [F"<{start}:{stop}>"]
                term.tf = term.freq / len(segList)
                term.title = ci.title
                term.word = word
                ret[word] = term
            else:
                ret[word].freq += 1
                ret[word].tf = term.freq / len(segList)
                ret[word].pos.append(F"<{start}:{stop}>")
        return ret
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class Term:
    def __init__(self) -> None:
        self.docId = 0
        self.title = ""
        self.pos = []
        self.word = ""

        self.freq = 0
        self.tf = 0
        
    def __gt__(self, right: "Term") -> bool:
        return self.docId > right.docId

    def __lt__(self, right: "Term") -> bool:
        return self.docId < right.docId

    def __ge__(self, right: "Term") -> bool:
        return self.docId >= right.docId

    def __le__(self, right: "Term") -> bool:
        return self.docId <= right.docId

    def __eq__(self, right: "Term") -> bool:
        return self.docId == right.docId
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

在这里插入图片描述

标题、内容的倒排索引构建

标题和内容的倒排索引构建方式相似，都是先进行分词，然后将分词加入到[word,PostingList]的字典当中。其中PostingList的实现方式为自增链表，方便后续进行布尔运算。

倒排索引实现的数据结构

布尔模型的倒排索引元存储在Term当中，其中Term的代码见[2.4.1]，同一单词对应的Term按照docId升序存储在PostingList当中，PostingList实现方式为自增链表，而word和PostingList之间的映射通过HashMap(Python自带的dict实现)实现。

    def __init__(self) -> None:
        self.contentIndex: DefaultDict[str,
                                       OrderedList] = defaultdict(OrderedList)
        self.titleIndex: DefaultDict[str,
                                     OrderedList] = defaultdict(OrderedList)
1
2
3
4
5

PostingList的实现

class ListNode:
    def __init__(self, term: Term) -> None:
        self.term = term
        self.next = None

class OrderedList:
    def __init__(self, head=None):
        self.head = head
        self.freq = 0
        self.idf = 0
        self.word = ""
        self.it = None

        self.rsv = 0.0
        
    def add(self, item: Term):
        current = self.head
        previous = None
        stop = False
        while current is not None and not stop:
            if current.term > item:
                stop = True
            else:
                previous = current
                current = current.next
        temp = ListNode(item)
        if previous is None:
            temp.next = self.head
            self.head = temp
        else:
            temp.next = current
            previous.next = temp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

在倒排索引中添加Term

    def _addTerm(self, target: str, word: str, term: Term):
        if target == "content":
            invertedIndex = self.contentIndex
        elif target == "title":
            invertedIndex = self.titleIndex
        else:
            raise Exception("Invalid target")
        if word not in invertedIndex:
            invertedIndex[word] = OrderedList()
            invertedIndex[word].freq = 1
            invertedIndex[word].idf = math.log10(
                len(docs) / (invertedIndex[word].freq + 1))
            invertedIndex[word].word = word
            invertedIndex[word].add(term)
        else:
            invertedIndex[word].freq += 1
            invertedIndex[word].idf = math.log10(
                len(docs) / (invertedIndex[word].freq + 1))
            invertedIndex[word].add(term)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

概率模型索引和概率模型索引构建

class InvertedIndex:

    def __init__(self) -> None:
        self.contentIndex: DefaultDict[str,
                                       OrderedList] = defaultdict(OrderedList)
        self.titleIndex: DefaultDict[str,
                                     OrderedList] = defaultdict(OrderedList)

        self.titleWordSet: Set[str] = set()
        self.contentWordSet: Set[str] = set()
        self.ciWordMap: Dict[int, Counter] = {}
        self.contentWordMap: Dict[str, set] = {}
        self.titleWordMap: Dict[str, set] = {}
        self.length: int = 0

        self.binContentWordMap: Dict[Tuple[str, str], set] = {}
        self.binTitleWordMap: Dict[Tuple[str, str], set] = {}
        self.binCiWordMap: Dict[Tuple[int, str], Counter] = {}
        self.binContentWordSet: Set[Tuple[str, str]] = set()
        self.binTitleWordSet: Set[Tuple[str, str]] = set()
        self.binLength: int = 0

        self.nlp: NLPTool = NLPTool()
        
    def _buildUniIndex(self, word: str, docId: int, target: str):
        if target == "content":
            if word not in self.contentWordMap:
                self.contentWordMap[word] = set([docId])
            else:
                self.contentWordMap[word].add(docId)
            self.length += 1
        elif target == "title":
            if word not in self.titleWordMap:
                self.titleWordMap[word] = set([docId])
            else:
                self.titleWordMap[word].add(docId)
            self.length += 1
        elif target == "ci":
            if word not in self.ciWordMap:
                self.ciWordMap[docId] = Counter({word: 1})
            self.ciWordMap[docId][word] += 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

布尔运算实现

布尔运算的实现基本思路是将布尔运算转化成集合运算，然后再利用PostingList升序的特性降低时间复杂度。其中AND运算对应集合的交运算，OR对应集合的并运算，ANDNOT对应集合的差运算。而ANDs和ORs则是AND运算和OR运算连续进行，但因为其运算符合交换律，所以可以使用优先队列降低其运算时间复杂度。

def union(p1: "OrderedList", p2: "OrderedList") -> "OrderedList":
    if not p1 or not p2:
        return p1 if p1 else p2
    ret = cur = ListNode(Term())
    i, j = p1.head, p2.head
    while i and j:
        if i.term < j.term:
            cur.next = ListNode(i.term)
            cur = cur.next
            i = i.next
        elif i.term > j.term:
            cur.next = ListNode(j.term)
            cur = cur.next
            j = j.next
        else:
            cur.next = ListNode(i.term)
            cur = cur.next
            i, j = i.next, j.next
    while i:
        cur.next = ListNode(i.term)
        cur = cur.next
        i = i.next
    while j:
        cur.next = ListNode(j.term)
        cur = cur.next
        j = j.next
    ret = OrderedList(ret.next)
    ret.rsv = p1.rsv + p2.rsv
    return ret
def unionAll(ps: List["OrderedList"]) -> "OrderedList":
    heapq.heapify(ps)
    while len(ps) > 1:
        heapq.heappush(ps, OrderedList.union(
            heapq.heappop(ps), heapq.heappop(ps)))
    return ps[0]
def intersect(p1: "OrderedList", p2: "OrderedList") -> "OrderedList":
    if not p1 or not p2:
        return OrderedList()
    cur = ret = ListNode(Term())
    i, j = p1.head, p2.head
    while i and j:
        if i.term < j.term:
            i = i.next
        elif i.term > j.term:
            j = j.next
        else:
            cur.next = ListNode(i.term)
            i, j = i.next, j.next
            cur = cur.next
    ret = OrderedList(ret.next)
    ret.rsv = p1.rsv + p2.rsv
    return ret
def intersectAll(ps: List["OrderedList"]) -> "OrderedList":
    heapq.heapify(ps)
    while len(ps) > 1:
        heapq.heappush(ps, OrderedList.intersect(
            heapq.heappop(ps), heapq.heappop(ps)))
    return ps[0]
def difference(p1: "OrderedList", p2: "OrderedList") -> "OrderedList":
    cur = ret = ListNode(Term())
    i, j = p1.head, p2.head
    while i and j:
        if i.term < j.term:
            cur.next = ListNode(i.term)
            i = i.next
            cur = cur.next
        elif i.term == j.term:
            i, j = i.next, j.next
        elif i.term > j.term:
            j = j.next
    ret = OrderedList(ret.next)
    ret.rsv = p1.rsv + p2.rsv
    return ret
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

自然语言检索

在本系统当中，自然语言的检索指的是对输入的某个特定的句子，根据某个模型判断这个句子是否在某个文章当中。对于布尔模型，因为其结构较为简单，所以支持标题和内容及混合检索，同时可以显示对应分词所在的位置。而概率模型和语言模型则是通过相似概率计算，来进行检索。

布尔模型检索

对于某一个句子，最简单的方法则是使用分词工具，将句子进行分词，然后使用AND操作符进行连接计算。具体代码如下：

单独单词的查询：

    def search(
            self,
            sentence: str,
            invertedIndex: InvertedIndex,
            mode: str) -> ResultSet:
        try:
            if mode == "content":
                index: DefaultDict[str,
                                   OrderedList] = invertedIndex.contentIndex
            elif mode == "title":
                index: DefaultDict[str, OrderedList] = invertedIndex.titleIndex
            else:
                raise ValueError("mode must be content or title")
            unformattedResult = OrderedList.intersectAll(
                [index[word] for word in jieba.lcut(sentence)])
            cur = unformattedResult.head
            ret = ResultSet()
            ret.expression = F"search {sentence} in BM"
            while cur:
                result = Result()
                result.id = cur.term.docId
                result.title = cur.term.title
                result.freq = cur.term.freq
                result.tf = cur.term.tf
                result.pos = cur.term.pos
                result.weight = Rank.tf(
                    invertedIndex, cur.term.word, cur.term, mode)
                result.rsv = unformattedResult.rsv
                ret.add(result)
                cur = cur.next
            return ret
        except KeyError:
            return ResultSet()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

将不同目标的结果结合

    def combineContentAndTitleResult(
            contentResult: "ResultSet",
            titleResult: "ResultSet") -> "ResultSet":
        ret = ResultSet()
        ret.expression = F"mix {contentResult.expression}"
        for key in contentResult.results.keys():
            if key in titleResult.results:
                ret.results[key] = contentResult.results[key]
                ret.results[key].weight = contentResult.results[key].weight * \
                    config.contentWeight + \
                    titleResult.results[key].weight * config.titleWeight
                ret.results[key].tf = contentResult.results[key].tf + \
                    titleResult.results[key].tf
                ret.results[key].pos = contentResult.results[key].pos + \
                    titleResult.results[key].pos
                ret.results[key].freq = contentResult.results[key].freq + \
                    titleResult.results[key].freq
            else:
                ret.results[key] = contentResult.results[key]
                ret.results[key].weight = contentResult.results[key].weight * \
                    config.contentWeight

        for key in titleResult.results.keys():
            if key not in contentResult.results:
                ret.results[key] = titleResult.results[key]
                ret.results[key].weight = titleResult.results[key].weight * \
                    config.titleWeight
        return ret
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

而对于文档标题的混合，则是通过集合取交集，权重乘以配置文件当中的权重获得。

    def BMSearch(
            self,
            sentence: str,
            invertedIndex: InvertedIndex) -> ResultSet:
        try:
            return ResultSet.combineContentAndTitleResult(
                self.search(sentence, invertedIndex, "content"),
                self.search(sentence, invertedIndex, "title")
            )
        except KeyError:
            return ResultSet()
1
2
3
4
5
6
7
8
9
10
11

计算原理

TF(Term Frequency)：词频（TF）表示词条（关键字）在文本中出现的频率。
其计算公式如下： ${tf}_{ij}=\frac{n_{ij}}{\sum\limits_{k} n_{k,j}}$

逆向文件频率 (IDF)
：某一特定词语的IDF，可以由总文件数目除以包含该词语的文件的数目，再将得到的商取对数得到。其计算公式如下 $idf_i=\log_{10}{\frac{|D|}{|{j:t_i \in d_j}|}}$

实现方式

布尔模型的Ranking是直接通过计算tf值获得。

    def tf(index: InvertedIndex, word: str, term: Term, mode: str) -> float:
        return term.tf
1
2

而tf和idf则是在构建索引的时候计算，具体见图2.2{reference-type=“ref”
reference=“fig:add-term”}

结果分析

执行命令：

serach "江南好" -t mix
1

得到结果：

在这里插入图片描述

使用show命令分别查看运行结果，发现都有"江南好"三个字。

再执行命令

serach "好江南" -t mix
1

得到运行结果

在这里插入图片描述

可以看到执行结果相同，说明布尔模型的执行结果与顺序无关。

将使用config命令将titleWeigh降低，可以看到权重排名发生了变化，短小的《忆江南》成为了权重最高的结果。

config titleWeight 0.1
serach "江南好" -t mix
1
2

在这里插入图片描述

概率模型检索

概率模型检索的基本思想则是通过计算词汇的条件概率

            if mode == "PM":
                ret.expression = F"search {sentence} in PM"
                for word in words:
                    for docId in invertedIndex.contentWordMap[word].union(
                            invertedIndex.titleWordMap[word]):
                        result = Result()
                        if docId not in ret.results:
                            result.id = docId
                            result.title = docs.cis[docId].title
                            result.content = docs.cis[docId].content
                            result.rsv = Rank.ci(invertedIndex, word)
                            result.weight = result.rsv
                        else:
                            result = ret.results[docId]
                            result.rsv += Rank.ci(invertedIndex, word)
                            result.weight = result.rsv
                        ret.add(result)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

计算原理

首先将document向量进行自然语言处理，转化为向量 $\vec{x}=(x_1,x_2\dots x_T)$ ,
其中 $x_i=1$ 表示 $x_i$ 在文档中， $x_i=0$ 表示 $x_i$ 不在文档当中；则

\begin{aligned} S c o r e & = \\ = O (R | q, d) = O (Q | q, x) \\ = \frac{P r (R = 1 | q, x)}{P r (R = 0 | q, x)} \\ = \frac{\frac{P r (R = 1 | q) P r (x | R = 1, q)}{P r (x | q)}}{\frac{P r (R = 0 | q) P r (x | R = 0, q)}{P r (x | q)}} \\ = O (R | q) \frac{P r (x | R = 1, q)}{P r (x | R = 0, q)} \end{aligned}

S core = = O (R ∣ q, d) = O (Q ∣ q, x) = \frac{P r ( R = 1∣ q , x )}{P r ( R = 0∣ q , x )} = \frac{\frac{P r ( R = 1∣ q ) P r ( x ∣ R = 1 , q )}{P r ( x ∣ q )}}{\frac{P r ( R = 0∣ q ) P r ( x ∣ R = 0 , q )}{P r ( x ∣ q )}} = O (R ∣ q) \frac{P r ( x ∣ R = 1 , q )}{P r ( x ∣ R = 0 , q )}

又因为对于所有文档

d

来说，

q

是一样的，所以

O (R ∣ q)

可以看做一个常量因此

\begin{aligned} S c o r e (q, d) & = \\ = \prod_{i = 1}^{T} \frac{P r (x_{i} | R = 1, q)}{P r (x_{i} | R = 0, q)} \\ = \prod_{i = 1}^{T} \frac{P r (x_{i} = 1 | R = 1, q)}{P r (x_{i} = 1 | R = 0, q)} \prod_{i = 0}^{T} \frac{P r (x_{i} = 0 | R = 1, q)}{P r (x_{i} = 0 | R = 0, q)} \end{aligned}

其中，令

\begin{aligned} p_{i} = P r (x_{i} = 1 | R = 1, q) \\ r_{i} = P r (x_{i} = 0 | R = 0, q) \end{aligned}

p_{i} = P r (x_{i} = 1∣ R = 1, q) r_{i} = P r (x_{i} = 0∣ R = 0, q)

则

\begin{aligned} S c o r e (q, d) & = \\ = \prod_{i = 1}^{T} \frac{p_{i}}{r_{i}} \prod_{i = 1}^{T} \frac{1 - p_{i}}{1 - r_{i}} \\ = \prod_{i = 1}^{T} \frac{p_{i} (1 - r_{i})}{r_{i} (1 - p_{i})} \times c o n s t a n t \\ \Rightarrow \prod_{i = 1}^{T} \frac{p_{i} (1 - r_{i})}{r_{i} (1 - p_{i})} \end{aligned}

S core (q, d) = = i = 1 \prod T \frac{p _{i}}{r _{i}} i = 1 \prod T \frac{1 - p _{i}}{1 - r _{i}} = i = 1 \prod T \frac{p _{i} ( 1 - r _{i} )}{r _{i} ( 1 - p _{i} )} \times co n s t an t \Rightarrow i = 1 \prod T \frac{p _{i} ( 1 - r _{i} )}{r _{i} ( 1 - p _{i} )}

对上式取对数得

\begin{aligned} R S V = \sum \log \frac{p_{i} (1 - r_{i})}{r_{i} (1 - p_{i})} = \sum c_{i} \\ c_{i} = \log \frac{p_{i} (1 - r_{i})}{r_{i} (1 - p_{i})} \end{aligned}

RS V = \sum lo g \frac{p _{i} ( 1 - r _{i} )}{r _{i} ( 1 - p _{i} )} = \sum c_{i} c_{i} = lo g \frac{p _{i} ( 1 - r _{i} )}{r _{i} ( 1 - p _{i} )}

在实验中（其中，相关性的判定方式为：关键字是否在标题中，在标题中则相关，否则不相关；）：

doc	relevant	Non-relevant	total
$x_i=1$	$s$	$n - s$	$n$
$x_i=0$	$S - s$	$N - n - S + s$	$N - n$
$s u m$	$S$	$N - S$	$N$

\begin{aligned} p_{i} = \frac{s}{S} \\ r_{i} = \frac{n - s}{N - S} \\ c_{i} = \log \frac{p_{i} (1 - r_{i})}{r_{i} (1 - p_{i})} \end{aligned}

p_{i} = \frac{s}{S} r_{i} = \frac{n - s}{N - S} c_{i} = lo g \frac{p _{i} ( 1 - r _{i} )}{r _{i} ( 1 - p _{i} )}

但实际情况中可能会出现 $p_i,r_i$ 为 $0$ 的情况，同时做平滑处理，计算方式变为：

\begin{aligned} p_{i} = \frac{s + 0.5}{S + 1} \\ r_{i} = \frac{n - s + 0.5}{N - S + 1} \\ c_{i} = \log \frac{p_{i} (1 - r_{i})}{r_{i} (1 - p_{i})} \\ R S V = \sum c_{i} \end{aligned}

p_{i} = \frac{s + 0.5}{S + 1} r_{i} = \frac{n - s + 0.5}{N - S + 1} c_{i} = lo g \frac{p _{i} ( 1 - r _{i} )}{r _{i} ( 1 - p _{i} )} RS V = \sum c_{i}

实现方式

为了求取相关及包含的文档，在本次实验当中通过构建词项与文档的字典进行索引。在计算过程中，相关则说明词项在标题所构建的字典当中；而存在则说明词项在内容所构建的索引中。具体的相关存在、相关不存在等关系则可以通过集合运算后求结果集长度获得。

结果分析

同布尔模型的结果分析一样，执行以下两条命令，观察执行结果。

search "江南好" -m pm
search "好江南" -m pm
1
2

在这里插入图片描述

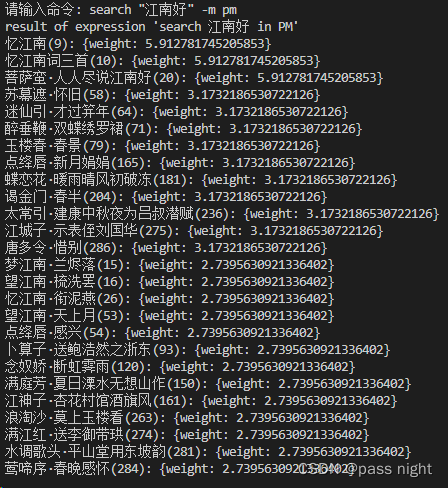
可以看到不仅仅执行结果相同，权重也相同，说明概率模型也与输入顺序无关。

一元混合语言模型检索

语言模型是通过计算词项的条件概率，混合模型指的是将在文档和文档集中的条件概率加权，一元指的是假设各个词项互相独立。而多个词汇则是通过直接求积进行连接。最后所得的结果作为权重参与排序。

计算原理

针对一个词项序列，我们可以使用链式法则 (Chain Rule) 去计算它的生成概率：
$P(t_1t_2t_3t_4)=P(t_1)P(t_2|t_1)P(t_3|t_1t_2)P(t_4|t_1t_2t_3)$
在一元语言模型中，假设每个词项之间两两独立则
$P(t_1t_2t_3t_4)=P(t_1)P(t_2)P(t_3)P(t_4)\\ p(t) = \prod P(t_i)$

对于文档其概率为
$P_d(q|M_d)=\prod\limits_{t\in q}\frac{tf_{t,d}}{L_d}$
而对于文档集，其概率为：
$P_c(q|M_c)=\frac{tf_{t,c}}{L_c}$
则其一元语言模型的加权加权概率为
$P=\lambda P_d + (1-\lambda)P_c$

实现方式

UMLE模型索引:

        self.titleWordSet: Set[str] = set()
        self.contentWordSet: Set[str] = set()
        self.ciWordMap: Dict[int, Counter] = {}
        self.contentWordMap: Dict[str, set] = {}
        self.titleWordMap: Dict[str, set] = {}
        self.length: int = 0

1
2
3
4
5
6
7

如下图所示，本系统通过构建每篇文档的词项计数器索引 $p_d$ 计算，通过构建整个文档的的词项索引进行 $p_c$ 计算

    def pc(index: InvertedIndex, word: str):
        tf = len(index.contentWordMap[word].union(index.titleWordMap[word]))
        ld = index.length
        return tf / ld
    
    def pd(index: InvertedIndex, word: str, docId: int):
        tf = index.ciWordMap[docId][word]
        ld = sum(index.ciWordMap[docId].values())
        return tf / ld   
1
2
3
4
5
6
7
8
9

结果分析

同布尔模型的结果分析一样，执行以下两条命令，观察执行结果。

search "江南好" -m umle
1

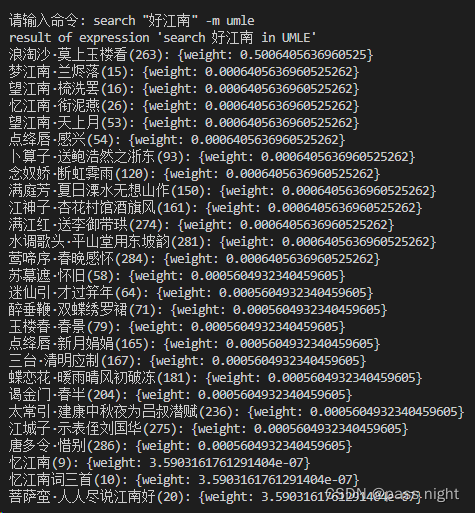
在这里插入图片描述](https://img-blog.csdnimg.cn/17717bd42d4b4d81ac088abd88c8165f.png)

可以看到不仅仅执行结果相同，权重也相同，说明一元混合语言模型也与输入顺序无关。

二元混合语言模型检索

二元混合语言模型相似于一元混合语言模型，但每一次考虑两个词项，所以在计算过程中需要同时考虑两个词项以及构建两个词项的索引。因为文档的第一个词项和最后一个词项没有前缀和后缀，所以添加分别作为第一个词项和第二个词项的前缀和后缀。

            elif mode == "BMLE":
                ret.expression = F"search {sentence} in BMLE"
                words = [""] + words + [""]
                for i in range(1, len(words)):
                    word = (words[i - 1], words[i])
                    for docId in invertedIndex.binContentWordMap[word].union(
                            invertedIndex.binTitleWordMap[word]):
                        result = Result()
                        if docId not in ret.results:
                            result.id = docId
                            result.title = docs.cis[docId].title
                            result.content = docs.cis[docId].content
                            result.binPc = Rank.binPc(invertedIndex, word)
                            result.binPd = Rank.binPd(
                                invertedIndex, word, docId)
                            result.bingram = Rank.bingram(
                                invertedIndex, word, docId)
                            result.weight = result.bingram
                        else:
                            result = ret.results[docId]
                            result.binPd *= Rank.binPd(invertedIndex,
                                                       word, docId)
                            result.bingram *= Rank.bingram(
                                invertedIndex, word, docId)
                            result.weight = result.bingram
                        ret.add(result)
            else:
                raise ValueError("mode must be PM, UMLE or BMLE")
        except KeyError:
            pass
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

计算原理

针对一个词项序列，我们可以使用链式法则 (Chain Rule) 去计算它的生成概率：
$P(t_1t_2t_3t_4)=P(t_1)P(t_2|t_1)P(t_3|t_1t_2)P(t_4|t_1t_2t_3)$
因为二元语言模型与前一个出现的词有关，所以对语料进行处理，加上头尾,

例如将’This is a sentence’转化为’This is a sentence’

则单独的概率
$P_i=\frac{c(word_1,word_2)}{c(word_1,any word)}$

为了求取 $c(word_1,word_2)$ ，程序在分词过程中将其构造为字典，并存储在[binWordMap]
变量当中，其余同一元混合语言模型

实现方式

同一元混合语言模型一样，只是将字典的key改成了连个词项组成的元组。

        self.binContentWordMap: Dict[Tuple[str, str], set] = {}
        self.binTitleWordMap: Dict[Tuple[str, str], set] = {}
        self.binCiWordMap: Dict[Tuple[int, str], Counter] = {}
        self.binContentWordSet: Set[Tuple[str, str]] = set()
        self.binTitleWordSet: Set[Tuple[str, str]] = set()
        self.binLength: int = 0
1
2
3
4
5
6

二元混合语言模型的权重计算

     def binPc(index: InvertedIndex, word: Tuple[str, str]):
        tf = len(index.binContentWordMap[word].union(
            index.binTitleWordMap[word]))
        ld = index.binLength
        return tf / ld
    def binPd(index: InvertedIndex, word: Tuple[str, str], docId: int):
        tf = index.binCiWordMap[docId][word]
        ld = sum(index.binCiWordMap[docId].values())
        return tf / ld
1
2
3
4
5
6
7
8
9

结果分析

同布尔模型的结果分析一样，执行以下两条命令，观察执行结果。


search "江南好" -m bmle
    search "好江南" -m bmle
1
2
3

在这里插入图片描述

可以看到不同于布尔模型、概率模型、一元混合语言模型，二元混合语言模型的执行结果与顺序相关。

模型对比

由上面对比可得，布尔模型、概率模型、一元混合模型搜索出来的结果相同。因为其基本原理决定，只要输入句子的分词有一项存在于目标文档当中则可出现在结果集。
而二元混合语言模型则需要词项对出现在文档当中才可出现在结果集当中，条件较为苛刻，因此计算出来的结果数较少。同时因为在开头和结尾补上了两个词项，所以对于检索的句子，还加上了一定的位置要求。
概率模型计算出来的权重较大的原因是概率模型是通过累加求和计算各个词项的的权重，且加上了平滑函数¹，所以权重分配较为均匀。而语言模型则是将权重相乘，而每项权重都小于1，所以最后相乘所获得的结果值非常小。

结果集处理

对于检索生成的结果，以结果类的形式存在于结果集当中。并在结果中通过面向对象的方式提供格式化和topK的及结合的功能。

class Result:
    def __init__(self) -> None:
        self.id = 0  # necessary
        self.title = ""  # necessary
        self.content = ""

        self.freq = 0
        self.tf = 0.0
        self.pi = 0.0
        self.ri = 0.0
        self.ci = 0.0
        self.rsv = 0.0
        self.pd = 1.0
        self.pc = 1.0
        self.unigram = 1.0
        self.binPd = 1.0
        self.binPc = 1.0
        self.bingram = 0.0

        self.weight = 0.0  # necessary

        self.pos = []
class ResultSet:
    def __init__(self) -> None:
        self.results: DefaultDict[int, Result] = defaultdict(Result)
        self.expression = "unknown expression"   
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

formatting

结果格式化显示文章的标题、id及权重。对于布尔模型的检索结果，可以显示出词项的位置。

    def format(self, showPos: bool = True) -> str:
        sb = [
            F"""{self.title}({self.id}): {{weight: {self.weight}"""]
        if showPos:
            sb.append(", pos: [")
            for pos in self.pos:
                sb.append(F"{pos}")
            sb.append("]")
        sb.append("}")
        return "".join(sb)
    
    def format(self, topK: int = -1, showPos: bool = True) -> str:
        if not self.results:
            return F"result of expression '{self.expression}' \nempty result"
        unformattedResults = self.topK(topK)
        return F"result of expression '{self.expression}' \n" \
            + "".join([result.format(showPos=showPos) +
                      "\n" for result in unformattedResults])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

topK

如图所示，topK使用堆排序算法，先将结果集转化(heapfiy)成一个堆，然后取其中k个最大值。倘若k为复数或大于结果集长度，则直接使用python内置的排序函数返回结果，以提高系统的执行效率。

def __lt__(self, other: "Result") -> bool:
    return (self.weight, self.id) < (other.weight, other.id)


def topK(self, topK: int) -> List[Result]:
    if topK > len(self.results) or topK < 0:
        return list(
            sorted(
                self.results.values(), key=lambda x: (
                    x.weight, -x.id), reverse=True))
    resultList = list(self.results.values())
    heapq.heapify(resultList)
    return heapq.nlargest(topK, resultList)	
1
2
3
4
5
6
7
8
9
10
11
12
13

用户界面

class Interface(cmd2.Cmd):

    def __init__(self) -> None:
        super().__init__()
        self.invertedIndex = InvertedIndex()
        self.invertedIndex.buildIndex()
        self.mode = "sentence"  # sentence or boolean
        self.target = "mix"  # content, title, mix
        self.prompt = "请输入命令: "
        self.intro = "Welcome to the search engine"
        self.engine = engine
1
2
3
4
5
6
7
8
9
10
11

用户界面采用的是Command Line
交互式界面。使用Cmd2库进行设计，支持tab补全及命令回滚等功能。可以使用help命令查看某个具体命令的帮助，使用quit退出程序。实验中实现的命令有以下几个：startSpider,config,calc,search,show

系统命令查看

输入以下命令查看系统命令

        help -v
1

在这里插入图片描述

输入以下命令查看某个具体命令

        help cmd
1

在这里插入图片描述

startSpider

startSpider命令的功能是爬取古诗词网中的宋词，并保存在Config.datasetPath路径下。

Usage: startSpider [-h]
        
        Start the spider
        
        optional arguments:
        -h, --help  show this help message and exit
1
2
3
4
5
6

在这里插入图片描述

config

config命令可以配置部分属性，如日志编码及混合查询的权重。同时也可以用于显示当前配置，具体介绍如下：

请输入命令: help config
Usage: config [-h] {logFileName, logLevel, logEncoding, datasetPath, contentWeight, titleWeight, lambda, show} {logFileName, logLevel, logEncoding, datasetPath, contentWeight, titleWeight, lambda, all}

configure the configuration
use show parameter to show the current configuration, if parameter is all or not specified, show all the configuration
use set parameter value to set the value of the parameter


positional arguments:
{logFileName, logLevel, logEncoding, datasetPath, contentWeight, titleWeight, lambda, show}
parameter to be changed
{logFileName, logLevel, logEncoding, datasetPath, contentWeight, titleWeight, lambda, all}
value to be set

optional arguments:
-h, --help            show this help message and exit
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

在这里插入图片描述

calc

calc功能为计算bool表达式，同search一样也支持topK和三种对象的选择。使用方法如下

请输入命令: help calc
Usage: calc [-h] [-n NUM] [-t {content, title, mix}] expression

calculate a boolean expression

positional arguments:
expression            boolean expression to be calculated

optional arguments:
-h, --help            show this help message and exit
-n, --num NUM         fetch the top n results
-t, --target {content, title, mix}
searching target
1
2
3
4
5
6
7
8
9
10
11
12
13

calc(标题模式)

search 江南 -t title
1

在这里插入图片描述

calc(内容模式)

calc "江南 OR 春 ANDNOT 忆" -t content
1

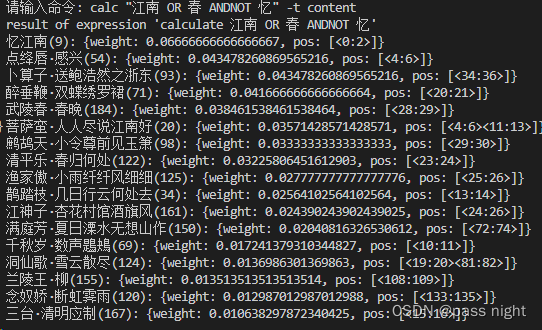
在这里插入图片描述

calc(混合模式)

calc "江南 AND 春 ORs 忆" -t mix
1

在这里插入图片描述

calc(混合模式+topK)

calc "江南 AND 春 ORs 江,夜 ORs 更,忆" -n 10 -t mix
1

在这里插入图片描述

search

search命令的功能为查询包含目标语句的宋词。使用方法如下：

请输入命令: help search
Usage: search [-h] [-t {content, title, mix}] [-n NUM] [-m {bm, pm, umle, bmle, cmp}] sentence

search for a sentence

positional arguments:
sentence              sentence to be searched

optional arguments:
-h, --help            show this help message and exit
-t, --target {content, title, mix}
searching target
-n, --num NUM         fetch the top n results
-m, --model {bm, pm, umle, bmle, cmp}
model to be used, bm for boolean model, pm for probabilistic model, umle for unigram model, bmle for bigram model, cmp for comparison model
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

search(BM-标题模式)

        search "江南" -t title
1

search(BM-内容模式)

    search "江南" -t content
1

在这里插入图片描述

search(BM-混合模式)

    search "江南" -t mix
1

在这里插入图片描述

search(BM标题模式+topK)

    search "江南" -t content -n 3
1

在这里插入图片描述

BM模型

        search "江南好" -m bm
1

PM模型

    search "江南好" -m pm
1

UMLE模型

    search "江南好" -m umle
1

在这里插入图片描述

BMLE模型

    search "江南好" -m bmle
1

在这里插入图片描述

对比模式

    search "江南好" -m cmp
1

在这里插入图片描述

展示宋词

在得到查询结果后，可以使用show命令来查看具体对应的宋词，以验证查询结果的正确性。

请输入命令: help show
Usage: show [-h] key

show the ci of the key

positional arguments:
key         key of ci to be shown

optional arguments:
-h, --help  show this help message and exit
1
2
3
4
5
6
7
8
9
10

在这里插入图片描述

若不加平滑函数，可能会出现类似于 $\log 0$ 这样的情况 ↩︎

相关阅读:
B2C在线教育商城--前后端分离部署
前端学习之Babel转码器
【熵与特征提取】从近似熵，到样本熵，到模糊熵，再到排列熵，包络熵，散布熵，究竟实现了什么？（第五篇）——“包络熵”及其MATLAB实现
给图片加自定义水印
Python按条件筛选、剔除表格数据并绘制剔除前后的直方图
剑指 Offer 18. 删除链表的节点 (Python 实现)
如何解决GitHub 访问不了？小白教程
JAVA的内存结构
C++11各种锁的具体使用
每周都知道｜工业互联网领域热点资讯 (10月2期)

原文地址：https://blog.csdn.net/apple_50661801/article/details/125900437