图的存储方式

邻接表（用链表的形式，直接存点，这种方法可以表示所有的图，包括有权值的图，就是多填一个条件嘛）
邻接矩阵

图的算法是比较简单的，问题在于图的表示方式比较多，对应的不同算法的代码是不一样的

这种问题的解决思路：用自己最喜欢用的表达图的方法，实现图的所有问题的算法，然后实际应用的时候，就是写一个两种表达图的方式之间的转换代码罢了。

标准图结构

一个点集
一个边集

点内容：

Int 点的数值
Int 点的入读
Int 点的出度
由这个点发散出去的边所链接的点的集合
由这个点发散出去的边的集合

边的内容

Int 权值
两个点（from，to）

接下来，不论是什么形式的图的输入，都修改成这个格式就好了。

有些内容（比如出度，入度）可能用不到，那就不填写就可以了

图和二叉树的区别：

图是可以有环的，所以要注意别环里面来来回回转。

图的宽度优先遍历

用队列来实现,但是需要设置一个set，保证流程中的节点不重复使用，防止没完没了了。

图的深度优先遍历

首先需要一个栈，一个set，一开始出发点进栈和set，然后处理这个初始点，之后开始循环，出栈，找这个出栈节点的邻居，如果在set里面，那无所谓，如果不在，那就出栈的点压栈，邻居也压栈，并且处理邻居节点，加入set。
就是仗着栈结构的先进后出，可这一条路径走到死

拓扑排序（工程中的节点事件依赖）

最后决定一个做事的顺序
需要注意的是，绝对绝对绝对不能有环，有环就可以直接除去了
解决方法，把完成的节点事件和他的路径都消去掉，然后找一个入读为0的点就可以了。
所以，我们需要一个map，存一个点的入度。
找所有入度为0的点，存在一个队列里面。
然后一个点，出队列，他所有的邻居的入度-1。重新开始遍历，直到这个队列空了。

针对无向图的一种算法，用来生成最小生成树。

最小生成树：权值最小的图的边的集合

生成最小树之——克鲁斯卡尔算法，

以边的角度来出发，把边按权值排序，只要不成环，就选。
唯一的问题：怎么判断成环
一开始每一个节点都是自己的一个集合。就是看from和to的两个节点是不是在和一个集合里的，是就不要，不是就要，并把这两个集合链接起来。

涉及到并查集（重点），但是时间有限，先不讲

我们自力更生，设置一个结构struct，里面有一个map，对应节点自己和节点所在的集合（list形式）。

初始化的时候，就是一个点，和只有这一个点的集合
然后要判断这两个点是不是在一个集合里面，就是利用map，看内存空间即可
最后，要能够合并集合，就是form和to对应的两个集合的合并，遍历随便一个（比如后者），然后把to的map里的list遍历出来，放到from的list里去，然后叫to的点的map也修改成指向from的合并好了的list即可。
这个方法比较省事，不过就是比较慢，不如并查集快。

生成最小树之——普利姆算法，PRIM

随机找一个起点，同时做一个集合，把起点放进去，每次选一条只有一个点在集合的边，把对应的邻居点拉进集合，不断循环
这样的方法的优势在于只需要一个哈希表就行，因为他不会像克鲁斯卡尔算法一样会有两个大团连接进来。
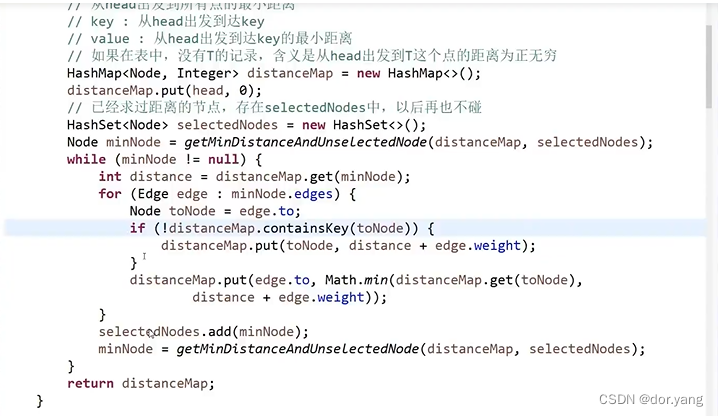
这里需要注意的一个问题是可能会有森林，本身就不连通。

迪杰斯特拉——单元最短路径算法

需要注意的是，千万不能有权值为负数的边