【27. 表达式求值（中缀表达式）】

表达式求值（中缀）

前提准备
需要开辟俩个栈，一个用于存放数字，另一个用于存放运算符。
需要用到unordered_map用来存放运算符的优先级。

步骤

（2 + 2 * 3）+ （4 * 5） 普通的式子就是中缀表达式

• 从头到尾读取中缀表达式的每个对象，对不同对象按不同的情况处理。

1. 运算数: 直接输出;
2. 左括号: 压入堆栈;
3. 右括号:将栈顶的运算符弹出并输出，直到遇到左括号(出栈，不输出)
4. 运算符:
    若优先级大于栈顶运算符时，则把它压栈;
    若优先级小于等于栈顶运算符时，将栈顶运算符弹出并输出;再比
较新的栈顶运算符，直到该运算符大于栈顶运算符优先级为止，然后将该运算符压栈;
5 若各对象处理完毕，则把堆栈中存留的运算符一并输!。 
1
2
3
4
5
6
7
8

图解

“表达式求值”问题，两个核心关键点：

（1）双栈，一个操作数栈，一个运算符栈；

（2）运算符优先级，栈顶运算符，和，即将入栈的运算符的优先级比较：

如果栈顶的运算符优先级低，新运算符直接入栈

如果栈顶的运算符优先级高，先出栈计算，新运算符再入栈

仍以1 + 2 + 3 * 4 * 5举例，看是如何利用上述两个关键点实施计算的。

首先，这个例子只有 + 和*两个运算符，所以它的运算符表是：

这里的含义是：

（1）如果栈顶是+，即将入栈的是+，栈顶优先级高，需要先计算，再入栈；

（2）如果栈顶是+，即将入栈的是*，栈顶优先级低，直接入栈；

（3）如果栈顶是*，即将入栈的是+，栈顶优先级高，需要先计算，再入栈；

（4）如果栈顶是*，即将入栈的是*，栈顶优先级高，需要先计算，再入栈；

一开始，初始化好输入的字符串，以及操作数栈，运算符栈。

一步步，扫描字符串，操作数一个个入栈，运算符也入栈。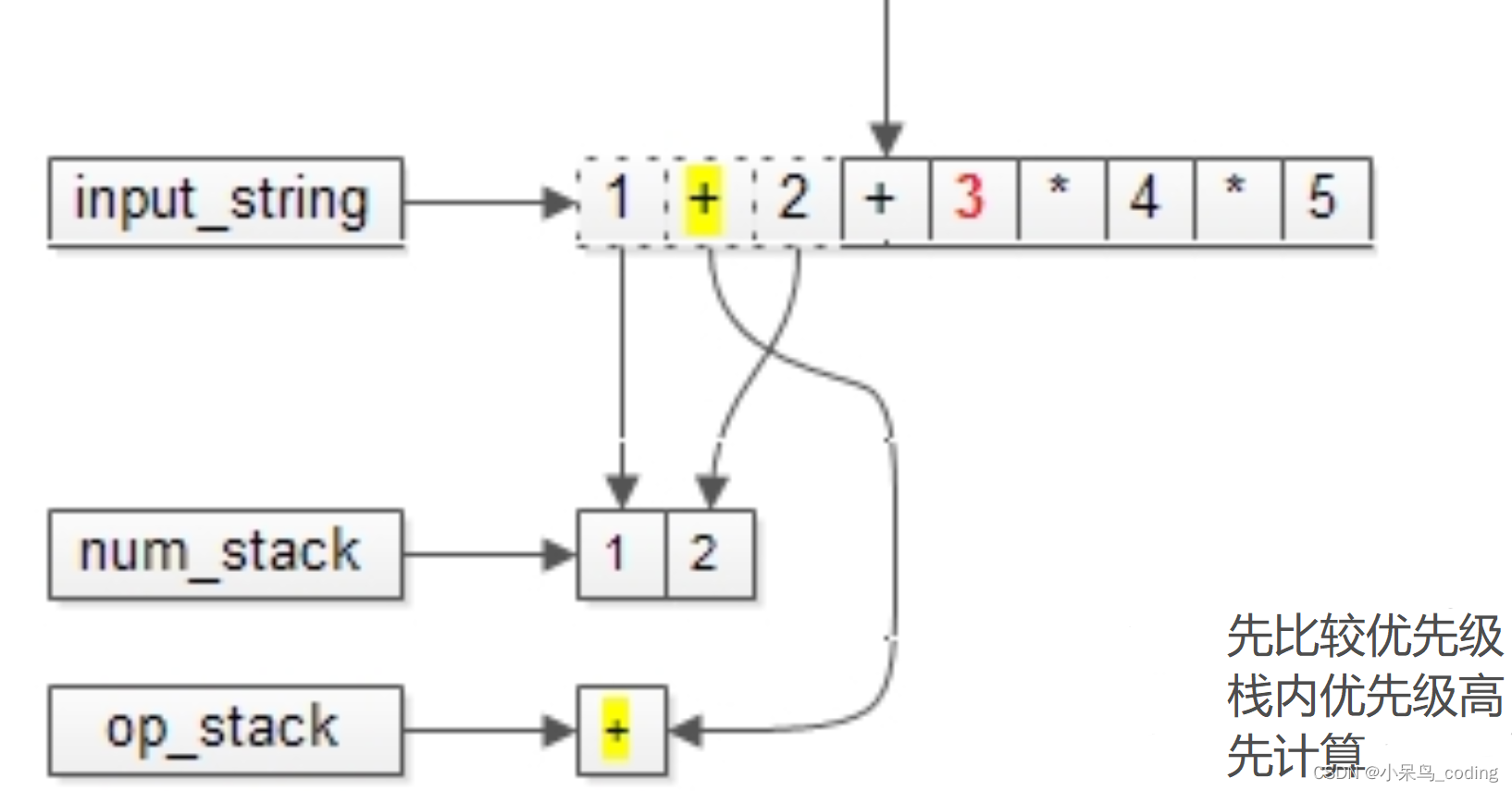

下一个操作符要入栈时，需要先比较优先级。

栈内的优先级高，必须先计算，才能入栈。

计算的过程为：

（1）操作数出栈，作为num2；

（2）操作数出栈，作为num1；

（3）运算符出栈，作为op；

（4）计算出结果；

（5）结果入操作数栈；

接下来，运算符和操作数才能继续入栈。下一个操作符要入栈时，继续比较与栈顶的优先级。

栈内的优先级低，可以直接入栈。

字符串继续移动。

又要比较优先级了。

栈内的优先级高，还是先计算（3*4=12），再入栈。

不断入栈，直到字符串扫描完毕。

不断出栈，直到得到最终结果3+60=63，算法完成。

题目

给定一个表达式，其中运算符仅包含 +,-,*,/（加 减 乘 整除），可能包含括号，请你求出表达式的最终值。

注意：

• 数据保证给定的表达式合法。
• 题目保证符号 - 只作为减号出现，不会作为负号出现，例如，-1+2,(2+2)*(-(1+1)+2) 之类表达式均不会出现。
• 题目保证表达式中所有数字均为正整数。
• 题目保证表达式在中间计算过程以及结果中，均不超过 2³¹−1。
• 题目中的整除是指向 0 取整，也就是说对于大于 0 的结果向下取整，例如 5/3=1，对于小于 0 的结果向上取整，例如 5/(1−4)=−1
• C++和Java中的整除默认是向零取整；Python中的整除//默认向下取整，因此Python的eval()函数中的整除也是向下取整，在本题中不能直接使用。

输入格式

共一行，为给定表达式。

输出格式

共一行，为表达式的结果。

数据范围

表达式的长度不超过 10₅。

输入样例：

(2+2)*(1+1)
1

输出样例：

8
1

代码

#include
#include
#include

using namespace std;


stack<int> num;      //存储运算数 
stack<char> op;     //存储运算符
                    //建立映射来判断运算优先级
unordered_map<char, int> cmp = {
    {'+', 1}, {'-', 1} , {'*', 2}, {'/', 2}
};
//模拟一次算术操作
void eval(void){
    int b = num.top();  num.pop();    //第二个操作数
    int a = num.top();  num.pop();    //第一个操作数
    char opr = op.top();    op.pop(); //运算符

    int x;                             //结果 
    //计算结果
    if(opr == '+')  x = a + b;
    else if(opr == '-') x = a - b;
    else if(opr == '*') x= a * b;
    else    x = a / b;
    num.push(x);                       //结果入栈
}

int main(){
    string str;
    cin >> str;

    for(int i = 0; i < str.size(); i++){
        char c = str[i];
        //读入运算数
        if(isdigit(c)){
            int j = i, x = 0;
            while( j < str.size() && isdigit(str[j])){
                //j++ 迭代不能忘 
                x = x *  10 + str[j ++] - '0';   //当输入的不是一个数而是22这种大于10的数，此时需要遍历整个字符，遇到符号位停止
            }
            num.push(x);
            //由于每轮循环有i++,我们需要倒指向最后一个数字
            i = j - 1;
            
        }else if( c == '(' ){
            //标记一下，括号内数据
            op.push(c);
            
         //括号特殊，遇到左括号直接入栈，遇到右括号计算括号里面的
        }else if( c == ')' ){
            //括号的优先级，先算括号
            while( op.size() && op.top() != '(' )   eval();
            //左括号可以弹出
            op.pop();
            
        }else{
            //得先把乘除法算了再算加减
            //这里必须得带等于号 我们这题都是正整数计算
            // 0 - 5 + 3 
            //如果不算，上式会被错误计算成 -8
            //待入栈运算符优先级低，则先计算
            while( op.size() && cmp[op.top()] >= cmp[c])    eval();
            //操作符入栈
            op.push(c);
        }
    }
  
    while(op.size())    eval();    //剩余的进行计算
    cout << num.top() << endl;     //输出结果
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

图片来源于网络
https://www.acwing.com/solution/content/40978/