一、K-means算法原理

聚类的概念:一种无监督的学习，事先不知道类别，自动将相似的对象归到同一个簇中。

K-Means算法是一种聚类分析(cluster analysis）的算法，其主要是来计算数据聚集的算法，主要通过不断地取离种子点最近均值的算法。

K-Means算法主要解决的问题如下图所示。我们可以看到，在图的左边有一些点，我们用肉眼可以看出来有四个点群，但是我们怎么通过计算机程序找出这几个点群来呢？于是就出现了我们的K-Means算法。

图解：

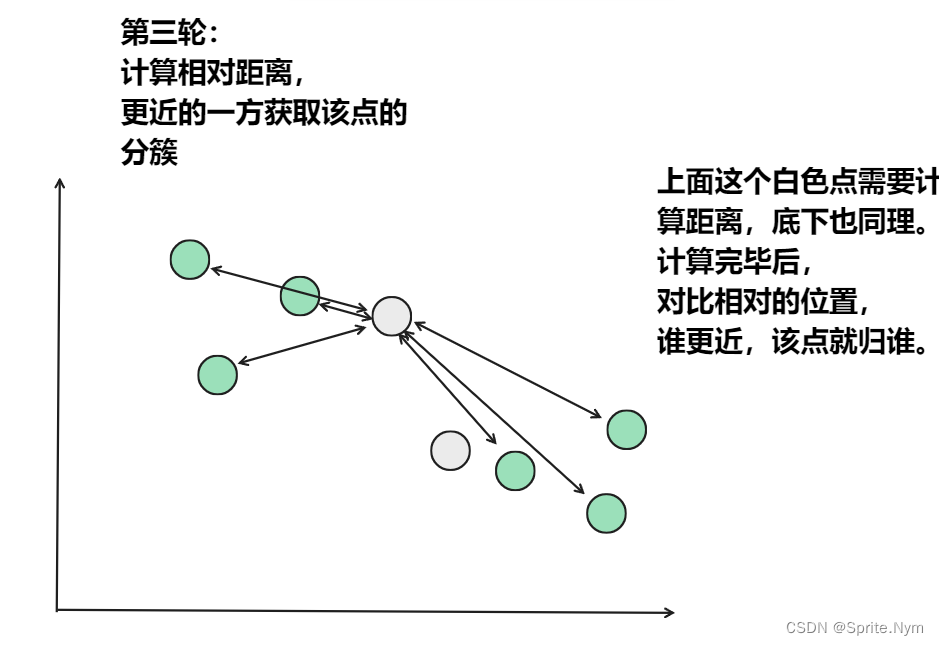
从上图中，我们可以看到，A，B，C，D，E是五个在图中点。而灰色的点是我们的种子点，也就是我们用来找点群的点。有两个种子点，所以K=2。
然后，K-Means的算法如下：

1. 随机在图中取K（这里K=2）个种子点。

2. 然后对图中的所有点求到这K个种子点的距离，假如点Pi离种子点Si最近，那么Pi属于Si点群。（上图中，我们可以看到A，B属于上面的种子点，C，D，E属于下面中部的种子点）

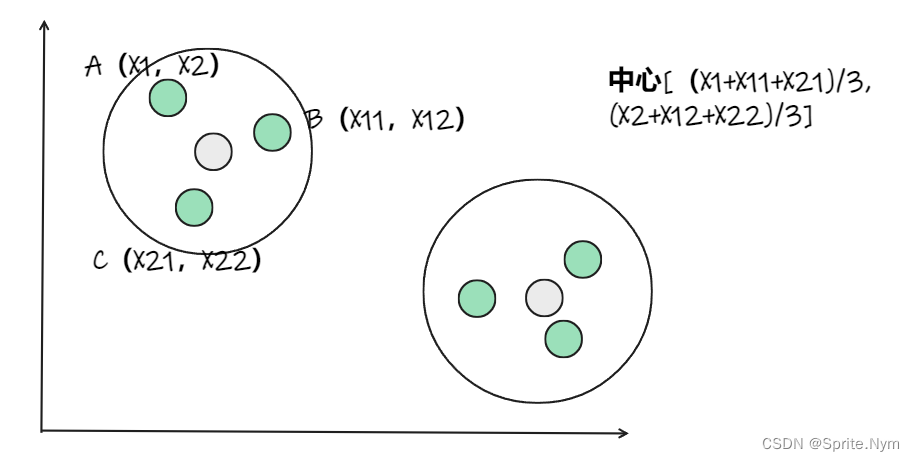
3. 接下来，我们要移动种子点到属于他的“点群"的中心。（见图上的第三步）

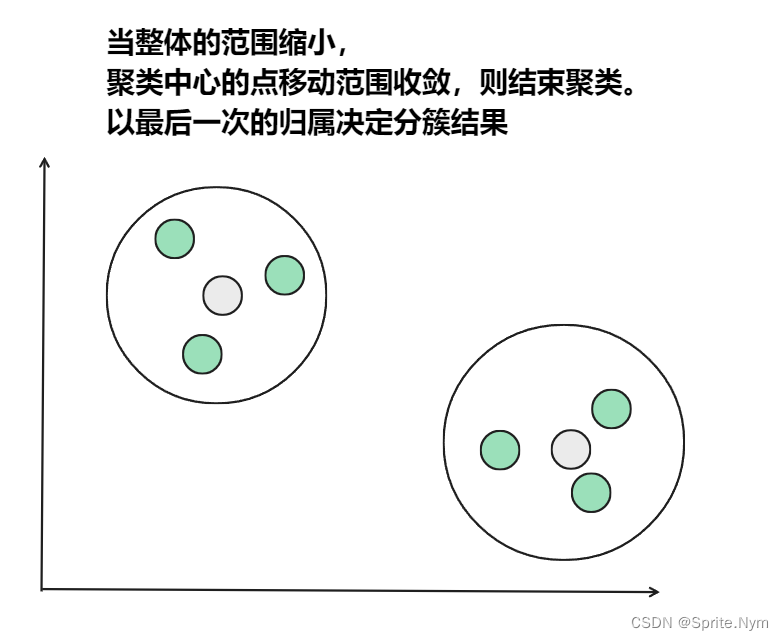
4. 然后重复第（2）和第（3）步，直到，种子点没有移动（我们可以看到图中的第四步上面的种子点聚合了A，B，C，下面的种子点聚合了D，E）。

总结：K-Means算法步骤：

1. 从数据中选择k个对象作为初始聚类中心；
2. 计算每个聚类对象到聚类中心的距离来划分；
3. 再次计算每个聚类中心。
4. 计算标准测度函数，直到达到最大迭代次数，则停止，否则，继续操作。
5. 确定最优的聚类中心。

K-means聚类方法总结

优点：

1. 解决聚类问题的经典算法，简单
2. 当处理大数据集时，该算法保持可伸缩性和高效率（与神经网络比）
3. 当簇近似正态分布时，效果较好

缺点：

1. 在簇的平均值可被定义的情况下才能使用，可能不适用于某些应用
2. 必须事先给出k（要生成簇的数目），而且对初值敏感，即对于不同的初值，可能会导致不同结果
3. 不适合非凸形状的簇或者大小差别很大的簇
4. 对噪声和孤立点敏感

聚类算法应用举例

1. 文档分类器
   根据标签、主题和文档内容将文档分为多个不同的类别。这是一个非常标准且经典的K-means算法分类问题。首先，需要对文档进行初始化处理，将每个文档都用矢量来表示，并使用术语频率来识别常用术语进行文档分类，这一步很有必要。然后对文档向量进行聚类，识别文档组中的相似性。
2. 客户分类
   聚类能过帮助营销人员改善他们的客户群（在其目标区域内工作)，并根据客户的购买历史、兴趣或活动监控来对客户类别做进一步细分。这是关于电信运营商如何将预付费客户分为充值模式、发送短信和浏览网站几个类别的白皮书。对客户进行分类有助于公司针对特定客户群制定特定的广告。
3. 保险欺诈检测
   机器学习在欺诈检测中也扮演着一个至关重要的角色，在汽车、医疗保险和保险欺诈检测领域中广泛应用。利用以往欺诈性索赔的历史数据，根据它和欺诈性模式聚类的相似性来识别新的索赔。由于保险欺诈可能会对公司造成数百万美元的损失，因此欺诈检测对公司来说至关重要。这是汽车保险中使用聚类来检测欺诈的白皮书。
4. 乘车数据分析
   面向大众公开的uber乘车信息的数据集，为我们提供了大量关于交通、运输时间、高峰乘车地点等有价值的数据集。分析这些数据不仅对uber大有好处，而且有助于我们对城市的交通模式进行深入的了解，来帮助我们做城市未来规划。

二、实战

重要参数：

• n_clusters：聚类的个数

重要属性：

• cluster_centers_：[n_clusters, n_features]的数组，表示聚类中心点的坐标
• labels_：每个样本点的标签

2.1 聚类实例

（1）聚类的基本使用

import numpy as np
import pandas as pd
import pyecharts.options as opts
import matplotlib.pyplot as plt
import seaborn as sns
from pyecharts.charts import Scatter

# 手动生成随机点做聚类
from sklearn.datasets import make_blobs

# 制作一个假的数据集
X, y = make_blobs(
    n_samples=150, 
    n_features=2,
    centers=3, 
    cluster_std=1.5, 
    random_state=2
)

# 下面都是在用pyecharts画画
def add_data(pic, X_data, y_data, symbol='circle', symbol_size=10):
    X_data = pd.DataFrame(X_data).copy()
    y_data = pd.Series(y_data).copy()
    for i in y_data.drop_duplicates():
        pic.add_xaxis(xaxis_data=X_data.loc[y_data == i].iloc[0:, 0].tolist())
        pic.add_yaxis(
            series_name=i,
            y_axis=X_data.loc[y_data == i].iloc[0:, 1].tolist(),
            symbol_size=symbol_size,
            symbol=symbol,
            label_opts=opts.LabelOpts(is_show=False)
        )

import pyecharts.options as opts
from pyecharts.charts import Scatter, Grid
from pyecharts.globals import ThemeType

m_scatter = Scatter(init_opts=opts.InitOpts(width="400px", height="400px", theme=ThemeType.LIGHT))
add_data(m_scatter, X, y)
m_scatter.set_series_opts()
m_scatter.set_global_opts(
    xaxis_opts=opts.AxisOpts(
        type_="value", 
        name="x1",
        splitline_opts=opts.SplitLineOpts(is_show=True)
    ),
    yaxis_opts=opts.AxisOpts(
        type_="value",
        name="x2",
        axistick_opts=opts.AxisTickOpts(is_show=True),
        splitline_opts=opts.SplitLineOpts(is_show=True)
    ),
    tooltip_opts=opts.TooltipOpts(is_show=False),
)
m_scatter.render_notebook()       
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

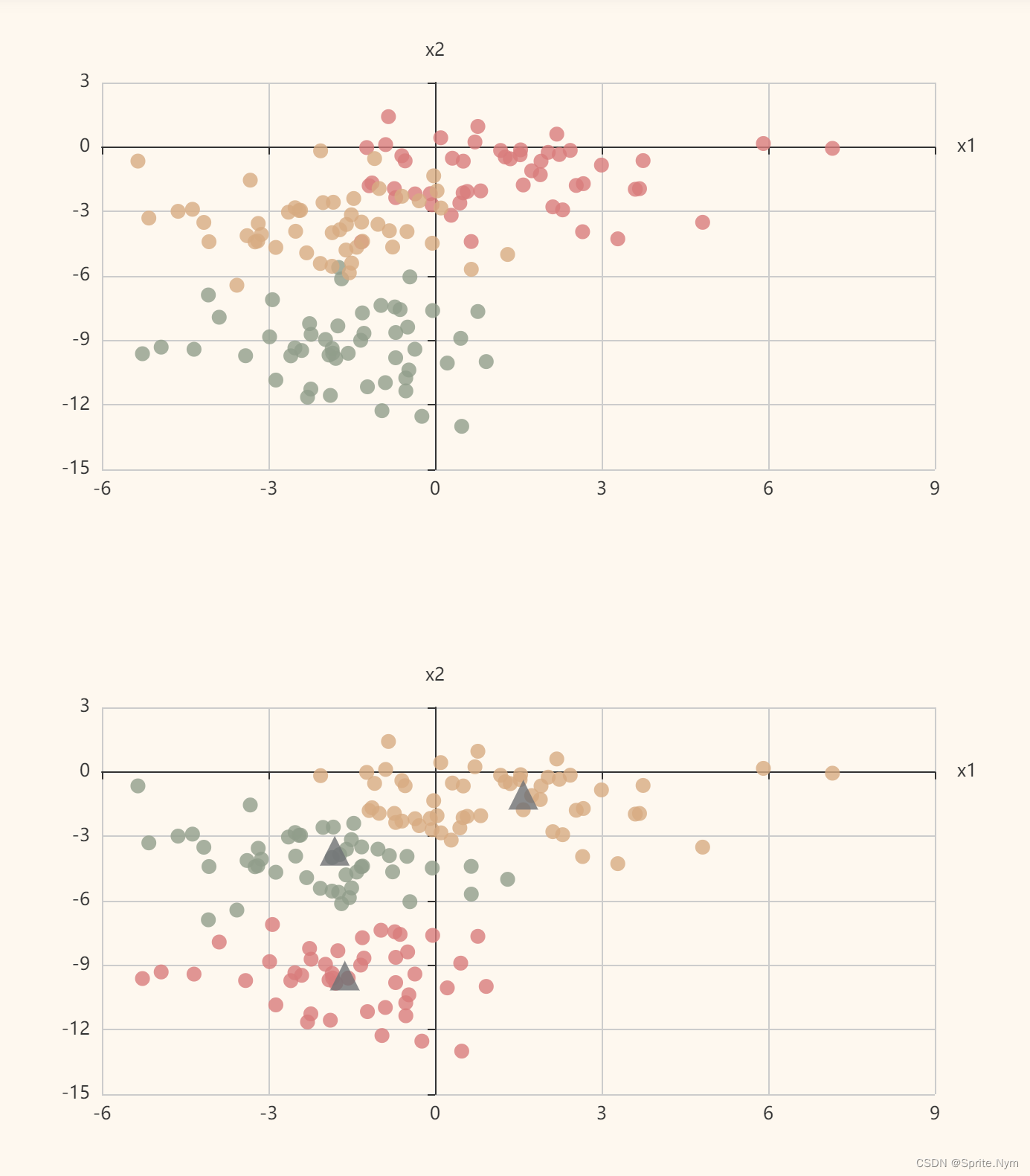
# 在聚类模块导入Kmeans
from sklearn.cluster import KMeans

# 第1步：实例化算法对象
# n_clusters 默认为8 默认8个随机点（初始点）分为8个簇 整形值
# k值应该怎么挑选：按业务需求来
km = KMeans(n_clusters=3)

# km.fit_predict()
# km.fit()
# km.predict()

# 第2步：开始预测
y_ = km.fit_predict(X)

# 获取聚类中心
cluster_centers = km.cluster_centers_
cluster_centers

"""
array([[ 1.58887503, -1.06495221],
       [-1.62473796, -9.4792349 ],
       [-1.80632868, -3.67173199]])
"""

# 继续画图
m_scatter2 = Scatter(init_opts=opts.InitOpts(width="400px", height="400px", theme=ThemeType.LIGHT))


add_data(m_scatter2, X, y)
add_data(m_scatter2, cluster_centers, [4, 4, 4], symbol='triangle', symbol_size=20)
m_scatter2.set_series_opts()
m_scatter2.set_global_opts(
    xaxis_opts=opts.AxisOpts(
        type_="value", 
        name="x1",
        splitline_opts=opts.SplitLineOpts(is_show=True)
    ),
    yaxis_opts=opts.AxisOpts(
        type_="value",
        name="x2",
        axistick_opts=opts.AxisTickOpts(is_show=True),
        splitline_opts=opts.SplitLineOpts(is_show=True)
    ),
    tooltip_opts=opts.TooltipOpts(is_show=False),
)
grid = Grid(init_opts=opts.InitOpts(width="700px", height="800px", theme=ThemeType.VINTAGE))
grid.add(m_scatter, grid_opts=opts.GridOpts(pos_bottom="60%"))
grid.add(m_scatter2, grid_opts=opts.GridOpts(pos_top="60%"))

grid.render_notebook()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

（2）足球队分群

data = pd.read_csv('data/AsiaZoo.txt', header=None)
data

data.columns=['国家', '2006世界杯', '2010世界杯', '2007亚洲杯']

from mpl_toolkits.mplot3d import Axes3D

# 设置seaborn和设置中文
sns.set_style(style='white')

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 制作特征X
X = data.iloc[:, 1:]
X

# 第1步：实例化
km = KMeans(n_clusters=3)

# 第2步：预测
y_ = km.fit_predict(X)

# 下面进行画图 3个特征 3个维度 - >  3D图
plt.figure(figsize=(10,6))

ax = plt.subplot(projection='3d')

ax.scatter3D(data['2006世界杯'],data['2010世界杯'],data['2007亚洲杯'],s=200,c=y_,alpha = 1)
ax.set_xlabel('2006世界杯')
ax.set_ylabel('2010世界杯')
ax.set_zlabel('2007亚洲杯')

plt.show()

# 需要往原来的数据集中增加一个column【类别】
data['类别'] = y_
data

# 如果我们需要把不同的国家和梯队进行输出
for i in range(3):
    print(' '.join(data[data['类别']==i]['国家'].tolist()))
"""
中国 伊拉克 卡塔尔 阿联酋 泰国 越南 阿曼 印尼
日本 韩国
伊朗 沙特 乌兹别克斯坦 巴林 朝鲜
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

附录：

1. RFM模型案例

2. 金融欺诈风险评估

2.2 聚类实践与常见错误

使用make_blobs创建样本点

• 第一种错误，k值不合适，make_blobs默认中心点三个

# 制作假数据集来应用KMeans
X, y = make_blobs(n_samples=150, n_features=2, centers=3, random_state=2, cluster_std=2)

# 底色，防止白色看不到
sns.set()

# 一会儿需要反复画图，因此可以对画图进行封装
# --需要在画图时进行传参X，y进行调用
def show_scatter(X, y):
    plt.scatter(X[:,0], X[:,1], c=y, cmap=plt.cm.Accent)
    plt.show()
    
# 调用函数进行测试
show_scatter(X, y)

# 第1步：实例化模型
km = KMeans(n_clusters=2)

# 第2步：预测
y_ = km.fit_predict(X)

# 封装一个X，y，y_函数，来显示实际上（True data）和预测的（KMeans）上的对比
def show_predict(X, y, y_):
    plt.figure(figsize=(12, 4))
    plt.subplot(121)
    plt.scatter(X[:,0], X[:,1], c=y, s=100, cmap=plt.cm.Accent)
    plt.title('True data')
    
    plt.subplot(122)
    plt.scatter(X[:,0], X[:,1], c=y_, s=100, cmap=plt.cm.afmhot)
    plt.title('KMeans')
    
    plt.show()
    
# 使用刚刚封装的函数来表现True data和KMeans的对比
show_predict(X, y, y_)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

• 第二种错误，数据偏差

  trans = [[0.6, -0.6], [-0.4, 0.8]]

  x2 = np.dot(X, trans)

# 故意增加偏差
trans = [[0.6,-0.6],[-0.4,0.8]]
X1 = np.dot(X,trans)

# 数据偏差情况
show_scatter(X1, y)
1
2
3
4
5
6

# 在这样条件下使用KMeans模型，观察结果
# 1.实例化
km2 = KMeans(n_clusters=3)
# 2.预测
y2 = km2.fit_predict(X1)

show_predict(X, y, y2)
1
2
3
4
5
6
7

• 第三个错误：标准偏差不相同cluster_std

  所以一定要在聚类之前，做数据的无量纲处理

# 元      万元
# 8000    0.8

# 刻意改变标准偏差之后的数据集
X3, y3 = make_blobs(n_samples=150, n_features=2, random_state=2, cluster_std=[1, 2, 4])

show_scatter(X3, y3)
1
2
3
4
5
6
7

# 1. 实例化
km3 = KMeans(n_clusters=3)
# 2. 预测
y3_ = km3.fit_predict(X3)

show_predict(X3, y3, y3_)
1
2
3
4
5
6

# 回忆：无量纲处理 sklearn中自带有一个preprocessing可以处理
from sklearn.preprocessing import MinMaxScaler, StandardScaler

ss_X3 = StandardScaler().fit_transform(X3)
ss_X3.std(axis=0)
1
2
3
4
5

• 第四个错误：样本数量不同

X, y = make_blobs(n_samples=1500, n_features=2, centers=3, random_state=5)

# 刻意构造样本不均衡 0 100个 1 35个 2 15个
XA = X[y==0][:100]
XB = X[y==1][:35]
XC = X[y==2][:15]

XX = np.concatenate((XA, XB, XC))
XX.shape

# 手动把标签添加上
y = np.array([0] * 100 + [1] * 35 + [2] * 15)

show_scatter(XX, y)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

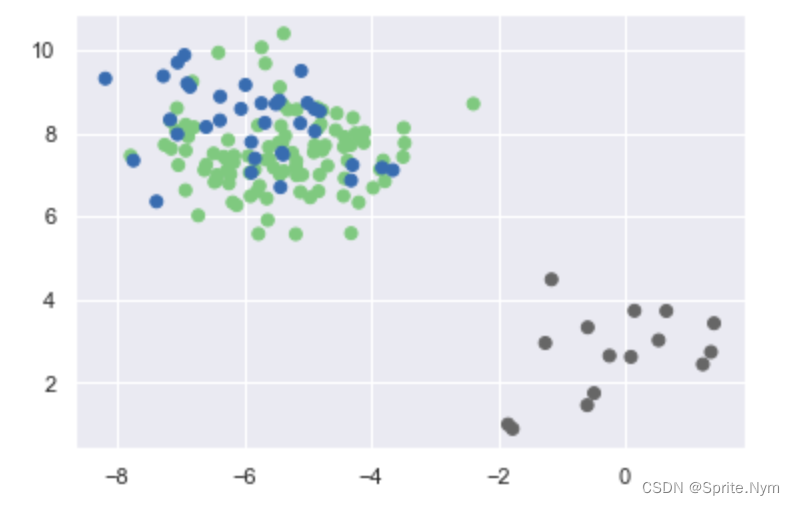
# 1. 实例化
km4 = KMeans(n_clusters=3)
# 2. 预测
y4_ = km4.fit_predict(XX)

show_predict(XX, y, y4_)
1
2
3
4
5
6

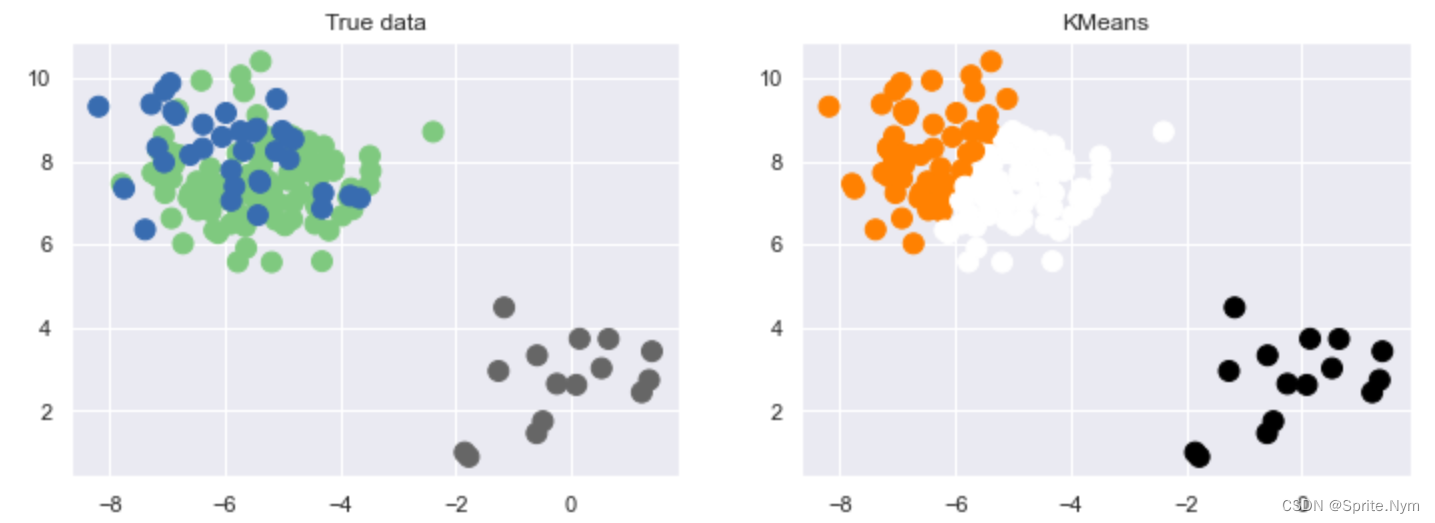
三、KMeans特征工程优化程度评价

某个点的轮廓系数定义为：

$$s=\frac{disMea{n}_{out}-disMea{n}_{in}}{max(disMea{n}_{out},disMea{n}_{in})}$$

其中$disMea{n}_{in}$为该点与本类其他点的平均距离，$disMea{n}_{out}$为该点与非本类点的平均距离。

该值取值范围为[-1, 1]，越接近1则说明聚类越优秀。

在sklearn中函数silhouette_score()计算所有点的平均轮廓系数，而silhouette_samples()返回每个点的轮廓系数。

from sklearn.metrics import silhouette_score # 返回所有点的平均轮廓系数
from sklearn.metrics import silhouette_samples # 返回每个点的轮廓系数
1
2

聚类的个数应该由业务需求给定，而不是根据轮廓系数来判断。

轮廓系数是在已知聚类个数的需求的前提下，针对特征工程处理的优化程度的评价。

# 导入轮廓系数
from sklearn.metrics import silhouette_score

# 1. 实例化
kmeans = KMeans(n_clusters=3)
# 2. 预测
y_ = kmeans.fit_predict(X)

# 使用轮廓系数进行评分
silhouette_score(X, y_)

# 定义一个函数，评判在不同的n_clusters上，轮廓系数以及图像
def show_cluster_edge(kmeans, X):
    xmin, xmax = X[:, 0].min(), X[:, 0].max()
    ymin, ymax = X[:, 1].min(), X[:, 1].max()
    
    x = np.linspace(xmin, xmax, 200)
    y = np.linspace(ymin, ymax, 200)
    xx, yy = np.meshgrid(x, y)
    
    kmeans.fit(X)
    
    X_test = np.c_[xx.ravel(), yy.ravel()]
    y_ = kmeans.predict(X)
    y1_ = kmeans.predict(X_test)
    
    plt.scatter(X_test[:,0], X_test[:,1], c=y1_, s=100, cmap=plt.cm.Accent)
    plt.scatter(X[:,0], X[:,1], c=y_, s=100, cmap=plt.cm.afmhot)
    
    plt.title('silhouette_score:%.4f'%(silhouette_score(X, y_)))
    plt.show()
    
    
kmeans = KMeans(n_clusters=3)
show_cluster_edge(kmeans, X)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35