深度学习3-神经网络和反向传播算法

神经元

神经元与感知器本质相同，但感知器的激活函数是跃迁函数；神经元的激活函数是sigmoid函数或双曲正切函数

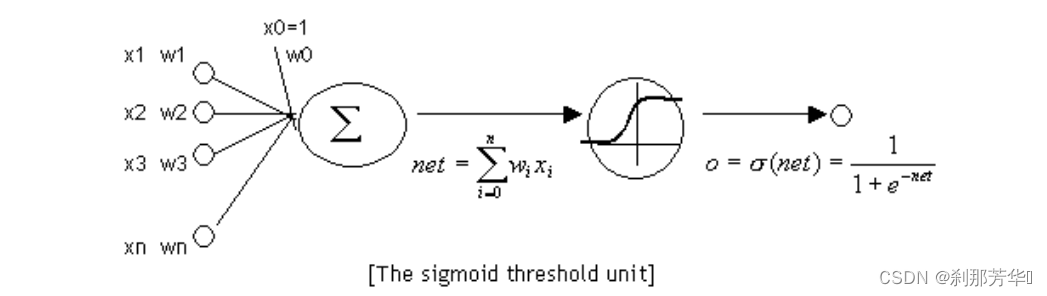
Sigmoid函数：

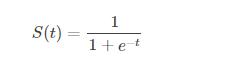
 tanh函数：

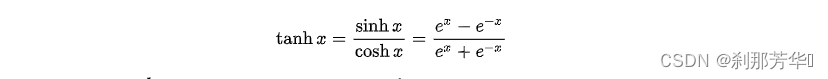
 神经网络的输出

        神经网络实际上就是一个输入向量x到输出向量y的函数：

 以全连接神经网络为例：

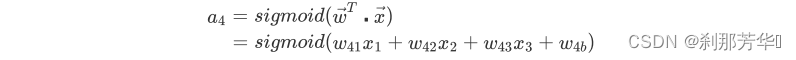
 通过线性代数的知识可以推导出：

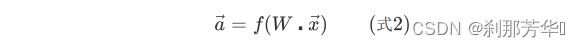
 向量a为某层输出向量，f是激活函数，W是权重矩阵，向量x为每层输入向量。以此类推，深层神经网络中，左侧输入向量左乘一个权重矩阵，得到一个新的向量，这个向量再作为输入向量左乘下一层权重矩阵，直到最后一层得到输出向量y。

神经网络的训练

超参数：神经网络的连接方式、网络层数、每层的节点数，超参数是人为设置的，而不是学习出来的。

反向传播算法：

由于计算某个节点的误差项，需要先计算每个与其相连的下一层节点的误差项，这就要求误差项的计算必须先从输出层开始，然后反向计算每个隐藏层的误差项，直到与输入层相连的隐藏层。所有节点误差项计算完成后，用式5更新权重。

假设每个训练样本为（向量x，向量t） ，其中向量x是训练样本的特征，而向量t是样本的目标值。

对于输出层第i个节点的误差项：

 对于隐藏层第i个节点的误差项：

 更新每个连接上的权值：

神经网络的实现 

 梯度检查

通过梯度检查判断参数wji是否正确，进而判断是否有bug