• 2022年暑假ACM热身练习3

    目录

    夹角有多大

    汉诺塔3/4

    选课时间

    龟兔赛跑

    Subset sequence

    红色病毒问题

    一个人的旅行

    小兔的棋盘

    RPG的错排

    Coin Change

    夹角有多大

    translation： 

            给定时、分、秒，要求你求出时针和分针之间的角度。

    problem：

    1. 时分秒也要实时匹配，也就是说，分钟走一点，也是会影响是针的角度的。同理，秒针也是。
    2. 当时卡在了角度要保证在【0,180】之间。假如时针走的很多，分针走的很少，那他们之间的角度比如为30度，但如果以圆点到 0 点位起始轴计算角度的话，那计算出来的结果是330，此时我想的是对180取模，可这样是得到的是150呀，那30和150之间还有转换，这....   反正对角度的问题很菜就是了..

    当角度k大于180时， k = 360 - k 

    1. // problem :  
    2.  
    3. #include 
    4. using namespace std;
    5. #define ll long long
    6. typedef pair<int, int> PII;
    7. #define pb push_back
    8. int main(){
    9.     int t; scanf("%d", &t);
    10.     while(t--){
    11.         double h, m, s; scanf("%lf %lf %lf", &h, &m, &s);
    12.         if(h >= 12)h -= 12;
    13.  
    14.         double k1 = (h + m / 60 + s / 3600) * 360 / 12;
    15.         double k2 = (m + s / 60) * 360 / 60; 
    16.  
    17.         double ans = fabs(k1 - k2);
    18.         if(ans > 180)ans = 360 - ans;
    19.         int res = ans;
    20.         printf("%d\n", res);
    21.     }
    22.  
    23.     return 0;
    24. }

    汉诺塔3/4

    汉诺塔4是在3的基础上添加了额外条件，在此先介绍一下汉诺塔3

       A          B          C 

     ——     ——     ——

    做递归的题，找对递归表达的状态是最关键的一步。

    比如这题的。

    设 solve(n) 表示 :   将A盘上的n个盘子借助 B 盘 放到 C盘   （其中AC盘是可以互换的）

    那么问题的求解可以表示为： solve(n) = solve(n - 1) + 1 + solve(n - 1) + 1 + solve(n - 1)

    其中的 + 1 操作是移动最底下的那个盘子。

    1. // problem :  
    2.  
    3. #include 
    4. using namespace std;
    5. #define ll long long
    6. typedef pair<int, int> PII;
    7. #define pb push_back
    8.  
    9. ll solve(int n){
    10.     ll ans = 0;
    11.     if(n == 1)return 2;
    12.     ll k = solve(n - 1);
    13.     ans += k;
    14.     ans++;
    15.     ans += k;
    16.     ans++;
    17.     ans += k;
    18.     return ans;
    19. }
    20.  
    21. int main(){
    22.     int n;
    23.     while(~scanf("%d", &n)){
    24.         printf("%lld\n", solve(n));
    25.     }
    26.  
    27.     return 0;
    28. }
    29.

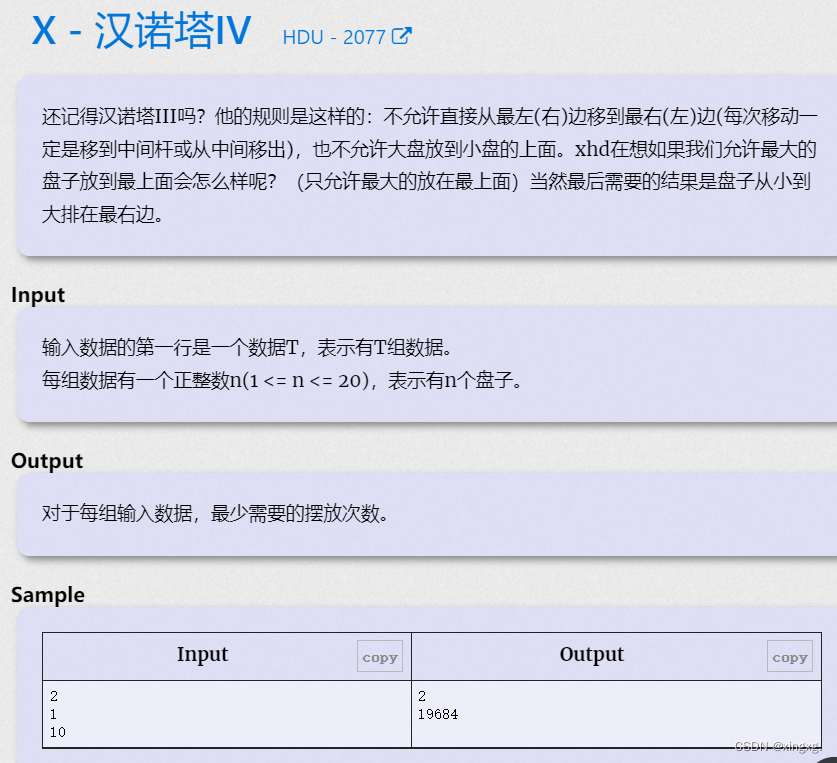
    汉诺塔3会做，汉诺塔4多了个条件，就不会了(ಥ﹏ಥ)

    translation:

            多了个条件，允许最大的盘子放在最上面。这里的题意（是指n个里最大，还是那一堆里最大的可以放最上面？？？,反正但是是挺疑惑）

    problem：

            这里只有第n个盘子能放在其他盘子上面， 比如n=5  ， 有一堆是  1 3  2     那3是不能放在最上面的！    所以我们移动上面的盘子时，还是要用 汉诺塔3的代码。

            用递归其实复杂度是不高的，也是O（n）的时间复杂度。而且还好理解很多，只不过代码篇幅可能较长 ( 那也只是我一步一步写，完全可以把代码合并

    1. // problem :  
    2.  
    3. #include 
    4. using namespace std;
    5. #define ll long long
    6. typedef pair<int, int> PII;
    7. #define pb push_back
    8.  
    9.  
    10. ll solve1(int n){
    11.     if(n == 1)return 2;
    12.     ll ans = 0;
    13.     ll k = solve1(n - 1);
    14.     ans += k;
    15.     ans++;
    16.     ans += k;
    17.     ans++;
    18.     ans += k;
    19.     return ans;
    20. }
    21.  
    22. ll solve2(int n){
    23.  
    24.     if(n == 1)return 2;
    25.     if(n == 2)return 4;
    26.     ll ans = 0;
    27.     ll k = solve1(n - 2);
    28.     ans += k;
    29.     ans += 2;
    30.     ans += k;
    31.     ans += 2;
    32.     ans += k;
    33.     return ans;
    34. }
    35. int main(){
    36.     int t; scanf("%d", &t);
    37.     while(t--){
    38.         int n; scanf("%d", &n);
    39.         printf("%lld\n", solve2(n));
    40.     }
    41.     return 0;
    42. }

    选课时间

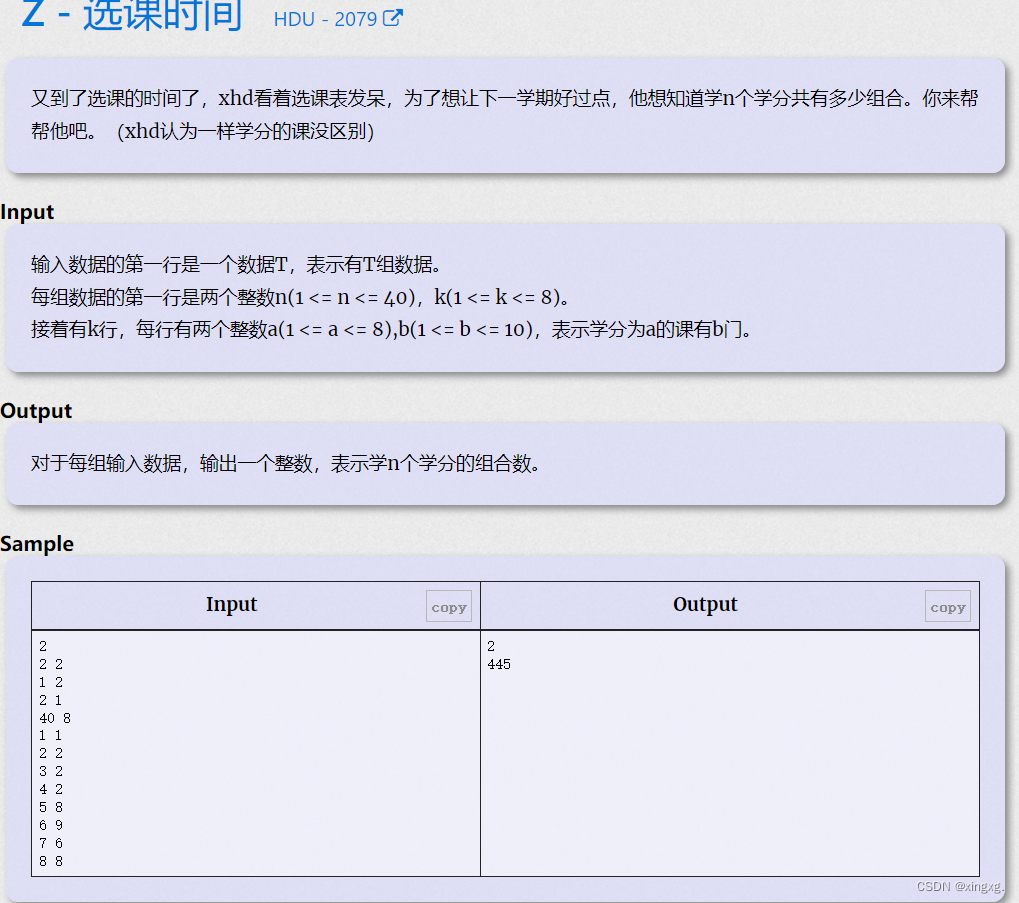
    problem：

             搜索、背包？  感觉偏背包的可能性较大

    solve：多重背包问题，但又有点特殊     要先枚举背包容量，否则会重复

     先给出AC代码：

    1. // problem :  
    2.  
    3. #include 
    4. using namespace std;
    5. #define ll long long
    6. typedef pair<int, int> PII;
    7. #define pb push_back
    8.  
    9. int f[45];
    10. int main(){
    11.     int t; scanf("%d", &t);
    12.     while(t--) {
    13.         int n, k; scanf("%d %d", &n, &k);
    14.         memset(f, 0, sizeof(f));
    15.         f[0] = 1;
    16.         while(k--) {
    17.             int a, b; scanf("%d %d", &a, &b);
    18.             for(int j = n; j >= a; --j)
    19.                 for(int m = 1; m <= b && j >= m * a; ++m)
    20.                     f[j] += f[j - a * m];
    21.  
    22.         } 
    23.         cout << f[n] << endl;
    24.     }   
    25.  
    26.     return 0;
    27. }

    为什么说特殊呢？因为这题不能用二进制拆分优化！

    1. for (int i = 1; i <= n; i++)
    2. 	for (int j = V; j >= w[i]; j--)
    3. 		for (int k = 1; k <= s[i] && k * w[i] <= j; k++)
    4. 			f[j] = max(f[j], f[j - w[i] * k] + v[i] * k);

    先枚举背包的容量，然后每种情况都放一遍        可以达到多重背包的效果。 

    先看看二进制拆分的代码

    1. for(int i = 1; i <= n; ++i){
    2.     int num = min(s[i], V / w[i]);
    3.     for(int k = 1; num; k <<= 1){
    4.         if(k > num)k = num;
    5.         num -= k;
    6.         for(int j = V; j >= k * w[i]; --j)
    7.             f[j] = max(f[j], f[j - k * w[i]] + k * v[i]);
    8.     }
    9. }

    这里是先枚举二进制数，再遍历背包的容量。V这个背包先放入1个，  下一轮2个...    ,最终1+2+...+2^n + k       达到背包存放的最大个数（num）。 为什么二进制数会叠加？因为较小的背包已经放入了物品。

    但我们“选课时间”这个题目是要先枚举背包的，要不然会有重复计算。

    那我们可以写先遍历背包，再枚举数量的二进制优化吗？答案是不行的。

    1. for(int i = 1; i <= n; ++i){
    2.     for(int j = V; j >= w[i]; --j){
    3.         int num = min(s[i], j / w[i]);
    4.         for(int k = 1; num; k <<= 1){
    5.             if(k > num)k = num;
    6.             num -= k;
    7.             f[j] = max(f[j], f[j - k * w[i]] + k * v[i]);
    8.         }
    9.     }
    10. }

     这份代码达到的是     V 这个背包容量 放1个能不能最大， 2 个 ……  2^n 个，能不能最大。但单个的2^n   又不能组成 num  个， 所以是不行的。

    龟兔赛跑

    problem： 一开始的想法是贪心，但要怎么贪呢？很关键的一点就是到达一个充电站之后，可以选中充电，或者选中不充电。当时没有去做，毕竟连考题的是贪心还是DP都没分清。

    solve： 本题用DP解决。关键点还是充电站要不要充电问题。还是感觉很巧妙吧！

    设  f[i] 为到第i个站点所花费的最少时间。接下来要确定状态转移方程；到第i个点，那肯定也经过了之前的点，那么  f[i]  = f[j] + time(i,j);     可是这怎么体现充电站要不要充电问题？ 

    j --> i  ，中间可能有站，所以中间的站就是不充电的站，j是充电的（除了起始点）。

    分析完也不难，关键就是：

    1. 先清楚这是个DP题；
    2. f[i] 代表什么意思；
    3. 列出状态转移方程。
    1. // problem :  
    2.  
    3. #include 
    4. using namespace std;
    5. #define ll long long
    6. typedef pair<int, int> PII;
    7. #define pb push_back
    8.  
    9. int l, n, c, t, p[105];
    10. double vr, vt1, vt2;
    11. double f[105];
    12. int main(){
    13.     while(~scanf("%d", &l)) {
    14.         scanf("%d %d %d", &n, &c, &t);
    15.         scanf("%lf %lf %lf", &vr, &vt1, &vt2);
    16.         for(int i = 1; i <= n; ++i)
    17.             scanf("%d", &p[i]);
    18.         p[n + 1] = l;
    19.         memset(f, 0, sizeof(f));
    20.         f[1] = 0;
    21.         for(int i = 2; i <= n + 1; ++i){
    22.             double minn = 1 << 30;
    23.             for(int j = 1; j < i; ++j){
    24.                 double time = f[j];
    25.                 if(j != 1)
    26.                     time += t;
    27.                 int len = p[i] - p[j];
    28.                 if(len > c)
    29.                     time += c * 1.0 / vt1 + (len - c) * 1.0 / vt2;
    30.                 else
    31.                     time += len * 1.0 / vt1;
    32.                 minn = min(minn, time);
    33.             }
    34.             f[i] = minn;
    35.         }
    36.         double res = l * 1.0 / vr;
    37.         if(res < f[n + 1])puts("Good job,rabbit!");
    38.         else puts("What a pity rabbit!");
    39.     }
    40.  
    41.     return 0;
    42. }

    Subset sequence

    红色病毒问题

    problem: 只能说是毫无头绪

    solve：涉及什么生成函数，直接记住公式了。    4^(n-1) + 2^(n-1)

    1. // problem :  
    2.  
    3. #include 
    4. using namespace std;
    5. #define ll long long
    6. typedef pair<int, int> PII;
    7. #define pb push_back
    8. const int p = 100;
    9. // ans=4^(n-1)+2^(n-1)
    10. ll rp(ll now, ll k){
    11.     ll res = 1;
    12.     for(; k; k >>= 1, now *= now, now %= p)
    13.         if(k & 1)
    14.             res *= now, res %= p;
    15.     return res;
    16. }
    17. int t;
    18. int main(){
    19.     while(~scanf("%d", &t) && t) {
    20.         for(int i = 1; i <= t; ++i){
    21.             ll n; scanf("%lld", &n);
    22.             printf("Case %d: %lld\n", i,(rp(4, n - 1) + rp(2, n - 1)) % p);
    23.         }
    24.         putchar(10);
    25.     }
    26.     return 0;
    27. }

    一个人的旅行

     这是个多起点，多重点的问题，而且，按照题目的样例，家离起点的距离都是0，那么我们就可以设置一个超级起点，这个起点到普通起点连一条权重为0的边，以超级起点为dijkstra搜索的起点即可。就算家里各个起点的距离不为0，甚至各不相同，也可以采用这个方法。（先假设距离都是0，再将最终算得的距离加上家离起点最短的距离即可。）

    problem：写代码时，  memset(head, 0, sizeof(127));   导致超时多次，

            其次，还有一种题型是  在地图上找一个点，求到  p1、p2、p3...pn  的最短路径和

    要对每个pi  做一次dijkstra

    1. // problem :  
    2.  
    3. #include 
    4. using namespace std;
    5. #define ll long long
    6. typedef pair<int, int> PII;
    7. #define pb push_back
    8. int t, s, d;
    9. struct edge{
    10.     int to, w, next;
    11. }e[100005];
    12. int cnt, head[1005], dis[1005];
    13. inline void makelist(int u, int v, int w){
    14.     e[++cnt].to = v;
    15.     e[cnt].next = head[u];
    16.     e[cnt].w = w;
    17.     head[u] = cnt;
    18. }
    19. struct node{
    20.     int id, _dis;
    21.     bool operator < (const node & a) const {
    22.         return _dis > a._dis;
    23.     }
    24. };
    25. bool vis[1005];
    26. void dijkstra(int _s){
    27.     dis[_s] = 0;
    28.     priority_queue q;
    29.     q.push({_s, dis[_s]});
    30.     while(!q.empty()){
    31.         node k = q.top();
    32.         q.pop();
    33.         int id = k.id;
    34.         if(vis[id])continue;
    35.         vis[id] = true;
    36.         for(int x = head[id]; x; x = e[x].next){
    37.             int to = e[x].to;
    38.             int w = e[x].w;
    39.             if(vis[to])continue;
    40.             if(w + dis[id] < dis[to]){
    41.                 dis[to] = w + dis[id];
    42.                 q.push({to, dis[to]});
    43.             }
    44.         }
    45.     }
    46. }
    47. void init(){
    48.     memset(vis, false, sizeof(vis));
    49.     memset(dis, 127, sizeof(dis));
    50.     memset(head, 0, sizeof(head));
    51.     cnt = 0;
    52.  
    53. }
    54. int main(){
    55.     while(~scanf("%d %d %d", &t, &s, &d)){
    56.         init();
    57.  
    58.         for(int i = 1; i <= t; ++i){
    59.             int x, y, time; scanf("%d %d %d", &x, &y, &time);
    60.             makelist(x, y, time);
    61.             makelist(y, x, time);
    62.         }
    63.  
    64.         for(int i = 1; i <= s; ++i){
    65.             int x; scanf("%d", &x);
    66.             makelist(1001, x, 0);
    67.         }
    68.  
    69.         int dd[1005];
    70.         for(int i = 1; i <= d; ++i)
    71.             scanf("%d", &dd[i]);
    72.         
    73.         int ans = 1 << 30;
    74.  
    75.         dijkstra(1001);
    76.         for(int i = 1; i <= d; ++i)
    77.             ans = min(ans, dis[dd[i]]);
    78.         
    79.         printf("%d\n", ans);
    80.     }
    81.  
    82.     return 0;
    83. }

    小兔的棋盘

    problem： 本身问题是不难的，甚至还有点简单，但就是样例给出的数据输出有点大病。

            姑且认为是考察观察能力了。    output:   第几个测试样例     棋盘大小    答案

    1. // problem :  
    2.  
    3. #include 
    4. using namespace std;
    5. #define ll long long
    6. typedef pair<int, int> PII;
    7. #define pb push_back
    8. int n;
    9. ll b[40][40];
    10. ll dfs(int x, int y){
    11.     if(b[x][y])return b[x][y];
    12.     if(x == n || y == n)return 1;
    13.     ll ans = 0;
    14.  
    15.     ans += dfs(x + 1, y);
    16.     if(y < x)
    17.         ans += dfs(x, y + 1);
    18.     return b[x][y] = ans;
    19. }
    20. int main(){
    21.     int c = 1;
    22.     while(~scanf("%d", &n)){
    23.         memset(b, 0, sizeof(b));
    24.         if(n == -1)break;
    25.         printf("%d %d %lld\n",c++, n, 2 * dfs(0, 0));
    26.     }
    27.  
    28.     return 0;
    29. }

    RPG的错排

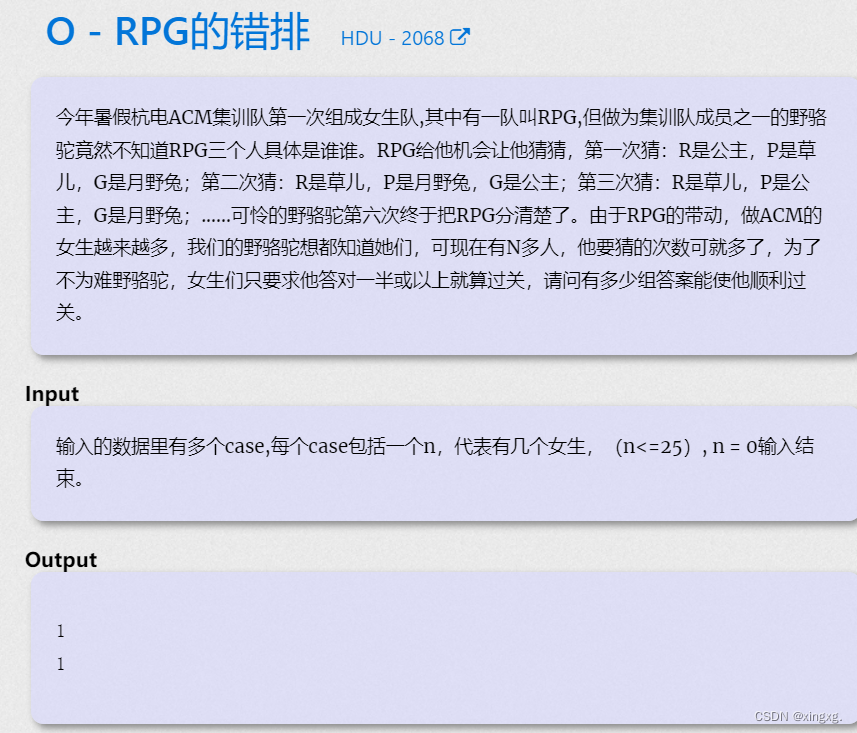
     problem：怎么说呢，这题错细节上了，有两个地方没有注意到

    1. factorial[21]  就会爆 long long     排列组合时，要先除
    2. m个人选对，那么就有n-m个人全错排，但是给写成了 m个人全错排

    solve：

            需要注意，选对n - 1个人  和 选对 n 个人是同一种情况，所以我们直接舍弃这两种情况，最后加1即可。

    1. // problem :  
    2.  
    3. #include 
    4. using namespace std;
    5. #define ll long long
    6. typedef pair<int, int> PII;
    7. #define pb push_back
    8. ll f[30];
    9. ll factorial[30];
    10.  
    11. void solve(){
    12.     // 阶乘
    13.     factorial[0] = 1;
    14.     for(int i = 1; i <= 25; ++i)
    15.         factorial[i] = factorial[i - 1] * i;
    16.  
    17.     // 全错排公式
    18.     f[1] = 0, f[2] = 1;
    19.     for(int i = 3; i <= 25; ++i)
    20.         f[i] = (i - 1) * (f[i - 1] + f[i - 2]); 
    21. }
    22. int main(){
    23.     int n;
    24.     solve();
    25.     while(~scanf("%d", &n) && n){
    26.         int k;
    27.         if(n & 1) k = (n+1)/2;
    28.         else k = n / 2;
    29.         ll ans = 0;
    30.  
    31.         for(int m = k; m <= n - 2; ++m){
    32.             // ans += factorial(n)/factorial(n - m)/factorial(m) * f[n - m];
    33.             ll c = 1;
    34.             for(int i = m + 1; i <= n; ++i)
    35.                 c *= i;
    36.             // c = factorial(n) / factorial(m)  --->  (m + 1) ... n 各位相乘
    37.             ans += c / factorial[n - m] * f[n - m];
    38.         }
    39.         ans++;
    40.         printf("%lld\n", ans);
    41.     }
    42.     return 0;
    43. }

    Coin Change

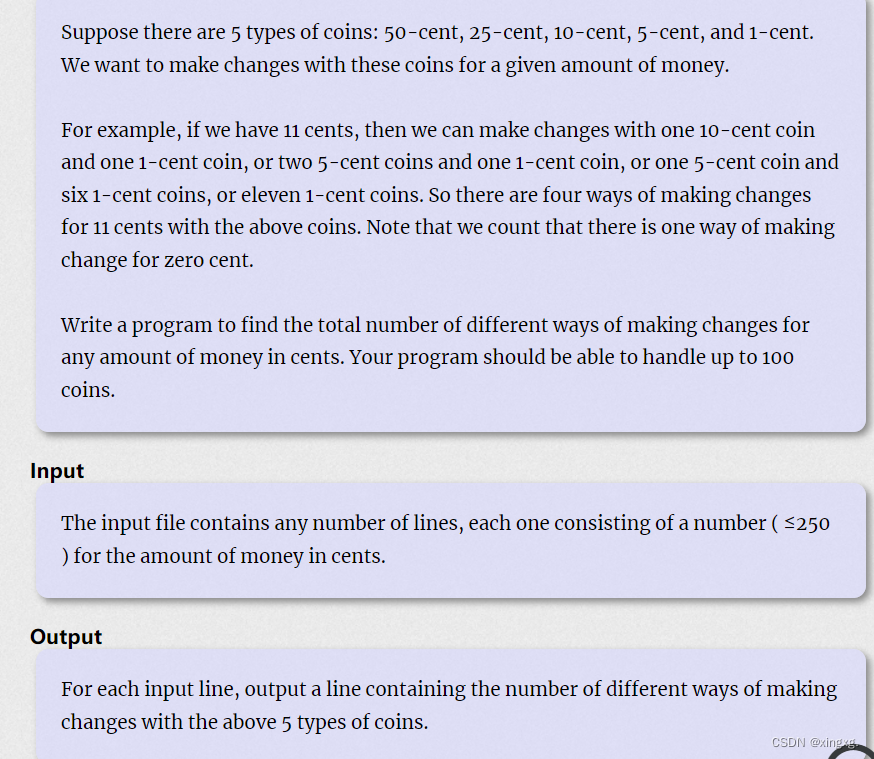
     题目大概就是跟找零钱花费最少的硬币差不多，  不过这里的题意是要求你求出有多少种凑够零钱的方式，并且所花费的硬币数量不能超过100个。

     没看到题目wa了的代码：

    1. void solve(){
    2.     f[0] = 1;
    3.     for(int i = 0; i < 5; ++i)
    4.         for(int j = type[i]; j <= 250; ++j)
    5.             f[j] += f[j - type[i]];
    6. }

    AC代码：（多加了一维数组，来限定条件）

    1. // problem :  
    2.  
    3. #include 
    4. using namespace std;
    5. #define ll long long
    6. typedef pair<int, int> PII;
    7. #define pb push_back
    8. int type[5] = {1, 5, 10, 25, 50};
    9. int f[255][105];
    10. void solve(){
    11.     f[0][0] = 1;
    12.     for(int i = 0; i < 5; ++i)
    13.         for(int j = 1; j <= 100; ++j)
    14.             for(int k = type[i]; k <= 250; ++k)
    15.                 f[k][j] += f[k - type[i]][j - 1];
    16. }
    17.  
    18. int main(){
    19.     int n;
    20.     solve();
    21.     while(~scanf("%d", &n)){
    22.         int ans = 0;
    23.         for(int i = 0; i <= 100; ++i)
    24.             ans += f[n][i];
    25.         printf("%d\n", ans);
    26.     }
    27.  
    28.     return 0;
    29. }
  • 相关阅读:
    Docker将镜像文件发布到私服库
    mysql基础知识篇（一）
    关于产品和消费的思考
    算法刷题日志——二叉树
    深度理解实分析：超越公式与算法的学习方法
    TCP/IP(十九)TCP 实战抓包分析(三)TCP 第一次握手 SYN 丢包
    RabbitMQ初识以及简单模式初步
    无法启动报，To install it, you can run: npm install --save @/components/iFrame/index
    计算机组成原理 | 中央处理器
    虚幻C+++基础 day2
  • 原文地址：https://blog.csdn.net/PURSUE__LIFE/article/details/125874043