---

题目

给定一个数组arr，长度为N，arr中的值不是0就是1。arr[i]表示第i栈灯的状态，0代表灭灯，1代表亮灯
每一栈灯都有开关，但是按下i号灯的开关，会同时改变i-1、i、i+1栈灯的状态
问题一：如果N栈灯排成一条直线,请问最少按下多少次开关？
i为中间位置时，i号灯的开关能影响i-1、i和i+1
0号灯的开关只能影响0和1位置的灯
N-1号灯的开关只能影响N-2和N-1位置的灯

解题思路

递归:从左到右模型

递归函数f(nextIndex,preStatus,curStatus)
nextIndex:当前位置的下一个位置,即当前来到的位置为nextIndex-1
preStatus:当前位置的前一个位置的状态
curStatus:当前位置的状态
潜台词0-i-1位置的灯是全亮的

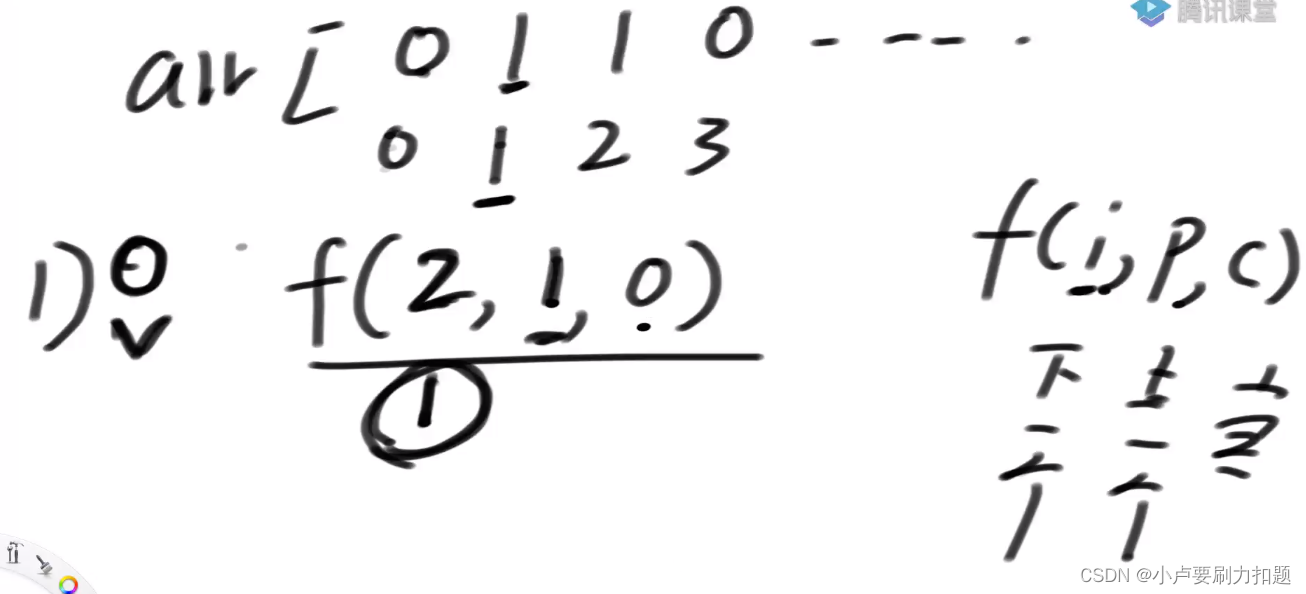
1)0位置按了开关.去1位置做选择,调用f(2,1,0)
2)0位置没按开关,调用f(2,0,1)
f返回值:
使之前做的决定都已经体现在参数上了，i位置怎么做决定能让整体的灯全亮，而且最少的开关数

递归代码

	public static int noLoopMinStep1(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		if (arr.length == 1) {
			return arr[0] ^ 1;
		}
		if (arr.length == 2) {
			return arr[0] != arr[1] ? Integer.MAX_VALUE : (arr[0] ^ 1);
		}
		// 不变0位置的状态
		int p1 = process1(arr, 2, arr[0], arr[1]);
		// 改变0位置的状态
		int p2 = process1(arr, 2, arr[0] ^ 1, arr[1] ^ 1);
		if (p2 != Integer.MAX_VALUE) {
			p2++;
		}
		return Math.min(p1, p2);
	}

	// 当前在哪个位置上，做选择，nextIndex - 1 = cur ，当前！
	// cur - 1 preStatus
	// cur  curStatus
	// 0....cur-2  全亮的！
	public static int process1(int[] arr, int nextIndex, int preStatus, int curStatus) {
		if (nextIndex == arr.length) { // 当前来到最后一个开关的位置
			return preStatus != curStatus ? (Integer.MAX_VALUE) : (curStatus ^ 1);
		}
		// 没到最后一个按钮呢！
		// i < arr.length
		if (preStatus == 0) { // 一定要改变
			curStatus ^= 1;
			int cur = arr[nextIndex] ^ 1;
			int next = process1(arr, nextIndex + 1, curStatus, cur);
			return next == Integer.MAX_VALUE ? next : (next + 1);
		} else { // 一定不能改变
			return process1(arr, nextIndex + 1, curStatus, arr[nextIndex]);
		}
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

递归改迭代

你当初0位置，如果按下了按钮，你是一条唯一的路径，一直决策到N没分叉
如果你0位置没有按下按钮，它依然是一条单独的分支， 走到N没有分叉

	public static int noLoopMinStep(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		if (arr.length == 1) {
			return arr[0] == 1 ? 0 : 1;
		}
		if (arr.length == 2) {
			return arr[0] != arr[1] ? Integer.MAX_VALUE : (arr[0] ^ 1);
		}
		int p1 = traceNoLoop(arr, arr[0], arr[1]);
		int p2 = traceNoLoop(arr, arr[0] ^ 1, arr[1] ^ 1);
		p2 = (p2 == Integer.MAX_VALUE) ? p2 : (p2 + 1);
		return Math.min(p1, p2);
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

进阶

如果N栈灯排成一个圈,请问最少按下多少次开关,能让灯都亮起来
i为中间位置时，i号灯的开关能影响i-1、i和i+1
0号灯的开关能影响N-1、0和1位置的灯
N-1号灯的开关能影响N-2、N-1和0位置的灯

题解

在无环问题中的递归函数增加两个参数
firstStatus:可能当前来到了i位置，当初0位置的状态是firststatus,因为来到最后一盏灯时是可以改变零的
endStatus:可能当前来到了i位置,当初0位置做完决定最后一个状态是endStatus
来到一个位置,它后面的位置是i, 一个普遍位置,告诉你当初0位置的状态firstStatus,最后一个位置的状态endStatus,
把这两个东西作为可变参数告诉你，你给我做决策
接下来你的下一个位置，你之前的状态跟你当前的状态跟刚才的函数一样

i:当前在i-1位置,是下一个位置
p:当前在i-1位置, i-2位置灯的状态
c:当前i-1位置，i-1位置灯的状态
fs: 0位置灯的状态
endS: N-1位置灯的状态

主函数调用4种分支
1)0按开关,1位置也按开关
2)0按开关,1位置不按开关
3)0不按开关,1位置不按开关
4)0不按开关,1位置按开关

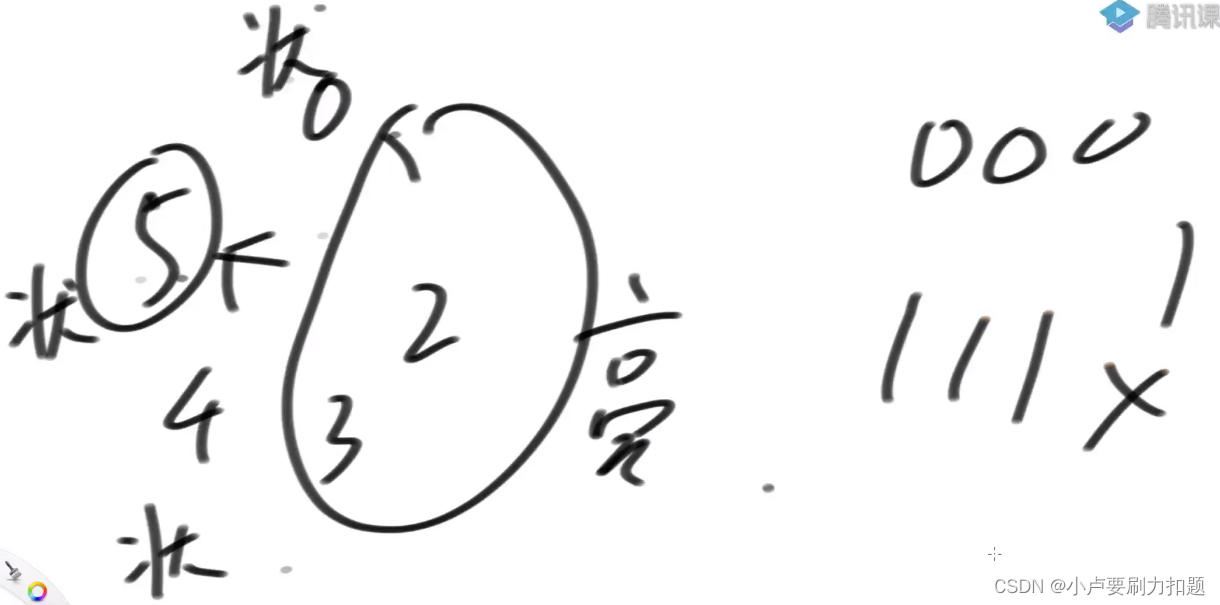
来到最后一个位置,现在知道0位置的状态,最后一盖灯的状态和前一盖灯的状态,三个状态都要一样,否则没法解决了

一个普遍位置的i，它将遵循的原则:
它前面的状态如果是亮的，它就不按
它前面的位置，如果是灭了，它一定要按
这是一个普适性质的i,但这个普适性在1位置就不能适用这个原则了。
客观上来讲1位置前面这个0位置不管是亮还是灭都可以，因为0位置还能被最后一个N-1位置搬回来

代码

	public static int loopMinStep1(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		if (arr.length == 1) {
			return arr[0] == 1 ? 0 : 1;
		}
		if (arr.length == 2) {
			return arr[0] != arr[1] ? Integer.MAX_VALUE : (arr[0] ^ 1);
		}
		if (arr.length == 3) {
			return (arr[0] != arr[1] || arr[0] != arr[2]) ? Integer.MAX_VALUE : (arr[0] ^ 1);
		}
		// 0不变，1不变
		int p1 = process2(arr, 3, arr[1], arr[2], arr[arr.length - 1], arr[0]);
		// 0改变，1不变
		int p2 = process2(arr, 3, arr[1] ^ 1, arr[2], arr[arr.length - 1] ^ 1, arr[0] ^ 1);
		// 0不变，1改变
		int p3 = process2(arr, 3, arr[1] ^ 1, arr[2] ^ 1, arr[arr.length - 1], arr[0] ^ 1);
		// 0改变，1改变
		int p4 = process2(arr, 3, arr[1], arr[2] ^ 1, arr[arr.length - 1] ^ 1, arr[0]);
		p2 = p2 != Integer.MAX_VALUE ? (p2 + 1) : p2;
		p3 = p3 != Integer.MAX_VALUE ? (p3 + 1) : p3;
		p4 = p4 != Integer.MAX_VALUE ? (p4 + 2) : p4;
		return Math.min(Math.min(p1, p2), Math.min(p3, p4));
	}

	
	// 下一个位置是，nextIndex
	// 当前位置是，nextIndex - 1 -> curIndex
	// 上一个位置是, nextIndex - 2 -> preIndex   preStatus
	// 当前位置是，nextIndex - 1, curStatus
	// endStatus, N-1位置的状态
	// firstStatus, 0位置的状态
	// 返回，让所有灯都亮，至少按下几次按钮
	
	// 当前来到的位置(nextIndex - 1)，一定不能是1！至少从2开始
	// nextIndex >= 3
	public static int process2(int[] arr, 
			int nextIndex, int preStatus, int curStatus, 
			int endStatus, int firstStatus) {
		
		if (nextIndex == arr.length) { // 最后一按钮！
			return (endStatus != firstStatus || endStatus != preStatus) ? Integer.MAX_VALUE : (endStatus ^ 1);
		}
		// 当前位置，nextIndex - 1
		// 当前的状态，叫curStatus
		// 如果不按下按钮，下一步的preStatus, curStatus
		// 如果按下按钮，下一步的preStatus, curStatus ^ 1
		// 如果不按下按钮，下一步的curStatus, arr[nextIndex]
		// 如果按下按钮，下一步的curStatus, arr[nextIndex] ^ 1
		int noNextPreStatus = 0;
		int yesNextPreStatus = 0;
		int noNextCurStatus =0;
		int yesNextCurStatus = 0;
		int noEndStatus = 0;
		int yesEndStatus = 0;
		if(nextIndex < arr.length - 1) {// 当前没来到N-2位置
			 noNextPreStatus = curStatus;
			 yesNextPreStatus = curStatus ^ 1;
			 noNextCurStatus = arr[nextIndex];
			 yesNextCurStatus = arr[nextIndex] ^ 1;
		} else if(nextIndex == arr.length - 1) {// 当前来到的就是N-2位置
			noNextPreStatus = curStatus;
			yesNextPreStatus = curStatus ^ 1;
			noNextCurStatus = endStatus;
			yesNextCurStatus = endStatus ^ 1;
			noEndStatus = endStatus;
			yesEndStatus = endStatus ^ 1;
		}
		if(preStatus == 0) {
			int next = process2(arr, nextIndex + 1, yesNextPreStatus, yesNextCurStatus,
					nextIndex == arr.length - 1 ? yesEndStatus : endStatus, firstStatus);
			return next == Integer.MAX_VALUE ? next : (next + 1);
		}else {
			return process2(arr, nextIndex + 1, noNextPreStatus, noNextCurStatus, 
					nextIndex == arr.length - 1 ? noEndStatus : endStatus, firstStatus);
					
		}
//		int curStay = (nextIndex == arr.length - 1) ? endStatus : arr[nextIndex];
//		int curChange = (nextIndex == arr.length - 1) ? (endStatus ^ 1) : (arr[nextIndex] ^ 1);
//		int endChange = (nextIndex == arr.length - 1) ? curChange : endStatus;
//		if (preStatus == 0) {
//			int next = process2(arr, nextIndex + 1, curStatus ^ 1, curChange, endChange, firstStatus);
//			return next == Integer.MAX_VALUE ? next : (next + 1);
//		} else {
//			return process2(arr, nextIndex + 1, curStatus, curStay, endStatus, firstStatus);
//		}
	}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

迭代

	public static int traceLoop(int[] arr, int preStatus, int curStatus, int endStatus, int firstStatus) {
		int i = 3;
		int op = 0;
		while (i < arr.length - 1) {
			if (preStatus == 0) {
				op++;
				preStatus = curStatus ^ 1;
				curStatus = (arr[i++] ^ 1);
			} else {
				preStatus = curStatus;
				curStatus = arr[i++];
			}
		}
		if (preStatus == 0) {
			op++;
			preStatus = curStatus ^ 1;
			endStatus ^= 1;
			curStatus = endStatus;
		} else {
			preStatus = curStatus;
			curStatus = endStatus;
		}
		return (endStatus != firstStatus || endStatus != preStatus) ? Integer.MAX_VALUE : (op + (endStatus ^ 1));
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24