-
mysql数据库设计理论
1. 什么是范式?
范式其实就是关系数据库规范程度的级别,举个我们生活中的例子,老师让打扫卫生,最低标准是扫地,二级标准是扫地+擦桌子,三级标准是扫地+擦桌子+擦玻璃,实际上在标准不断上升的过程中,首先高一级的标准是满足低一级标准的,范式也是如此,只不过它的标准描述的是数据库规范化的程度罢了。数据库中的范式有1NF , 2NF , 3NF , BCNF , 4NF,5NF(本文不讨论)。它们之间的关系1NF < 2NF < 3NF < BCNF < 4NF(默认越大 级别越高)。
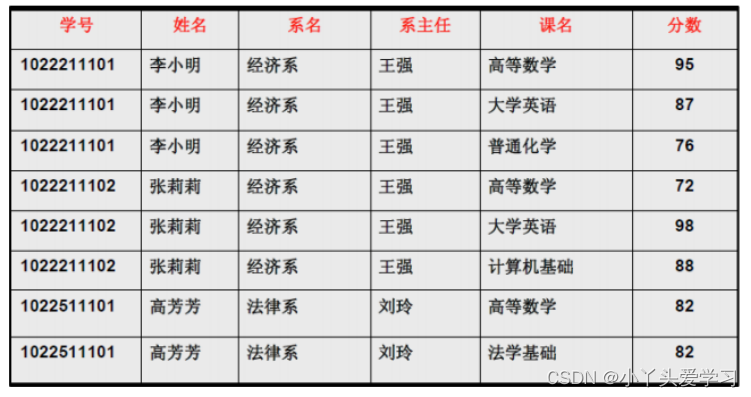
这个例子有下面的关系
(学号,课名)->分数
学号->姓名
学号->系名
系名->系主任
注:A->B:理解为A属性可以唯一确定B属性。这个例子会在说第二范式和第三范式的时候被逐步优化。
2.第一范式(1NF)
数据库表的每一列都是不可再分的原子数据项,它是一个关系型数据库的最低标准,如果不满足第一范式,那么这个数据库就不是关系型数据库。如下所示:
地址:5部分
省,市,区/县 —》街道/乡镇 ----》详细地址
地址:
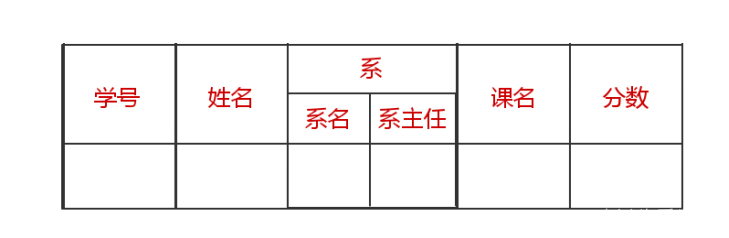
这个表我们无法在数据库中直接创建,因为它的系这一列,既有系名又有系主任,产生了冲突,如果作出调整,使它符合第一范式,那么应该是这样的:

但是即使这样,数据库中还是会存在诸如插入、删除、数据冗余等异常。比如针对下面的表:
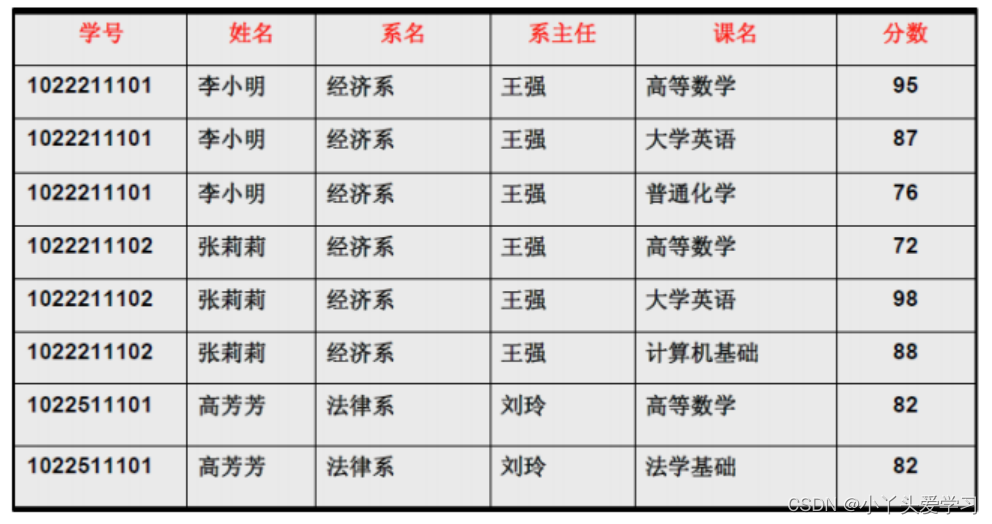
数据冗余:可以看到姓名、系名和系主任这三列冗余非常大。
插入异常:如果目前开设了计算机系,但是尚未招生,那么计算机系是无法插入到表的系名中的,(学号,课名)是主属性,不能为空。
删除异常:如果经济系的学生全部毕业了,在删除所有学生的时候,会将经济系一并删除因此这个数据库的设计是有缺陷的,为了优化它,我们继续到第二范式。在说第二范式之前,我们先来说几个重要的概念。
几个重要的概念。
函数依赖
函数依赖:在一张表中,如果给定A属性(或属性组)的值,一定能唯一确定B属性的值,那么就说B依赖于A属性(或属性组),记作A->B,比如给定学号,就能确定姓名,一个学号一定能确定一个姓名,就这么简单,是不是似曾相识?对,我们在第二部分中说那个贯穿全文的例子的时候其实已经用到这个概念了。
完全函数依赖
完全函数依赖:在函数依赖的基础上,我们的A属性是一个属性组,只有这个属性组中的全部属性才能确定唯一的B属性,A的任何一个子集都不可以。比如(学号,课名)->成绩,而单独的学号或者课名都不能确定成绩,这就叫完全函数依赖。
部分函数依赖
部分函数依赖:和完全函数依赖相比,A属性组中的部分属性就能确定B属性,其它属性可有可无,比如(学号,课名)->姓名,其实只要学号就可以了,这样的依赖就叫部分函数依赖。
传递函数依赖
传递函数依赖:如果A->B,B->C,并B不能->A(防止直接A->C),那么我们可以得出结论A->C,叫做C传递函数依赖A。比如学号->系名,系名->系主任,并且(系名不能决定学号),所以系主任传递函数依赖学号。
码
码:一个属性或者属性组,使得整个关系中除过此属性或者属性组之外的其余属性都完全函数依赖于它,那它就是码。例如(学号,课名),它们两个的组合可以将其他所有的属性都决定了,(学号,课名)->分数,学号->姓名,学号->系名,学号->系名->系主任,所以(学号,课名)就是这个关系中的一个码,那这个关系中还有别的码吗? 谁知道呢,但我们的分析过程应该是这样的:从一个属性一直到n个属性全部来一遍。
一个属性:学号,姓名,系名,系主任,课名,分数。找反例即可:学号不能决定分数,(必须要课名),姓名什么也决定不了,系名只能决定系主任,课名也决定不了什么,分数一样。所以一个属性中肯定是没有码的。
两个属性:(学号,姓名),(学号,系名),(学号,系主任),(学号,课名),(学号,分数),(姓名,系名),(姓名,系主任),(姓名,课名),(姓名,分数),(系名,系主任),(系名,课名),(系名,分数),(系主任,课名),(系主任,分数),(课名,分数)。呼~终于完了,我们再进行分析,发现只有(学号,课名),这个组合与其他的关系来说是完全函数依赖。也就是它们是一个码。
好吧,只能这样吗?对,只能这样,其实有一些能减少工作量的方法,比如如果我们在分析两个属性时已经确定(学号,课名)是码,那么在以后的分析中,如果包含(学号,课名)的那就一定不是码,因为要完全函数依赖。比如(学号,课名,系名)就不用分析了。其他的方法大家自己总结吧。
主属性:所有的码中包含的属性都是主属性。
非主属性:除过码中包含属性之外的属性。呼呼~,返过头再看一遍,我们要向第二范式出发了。
3.第二范式(2NF)
在第一范式的基础之上,确保每列和主键相关。
主键:行数据的唯一标识。 每个表描述一件事情(一种类型的对象)
在第一范式基础上,消除非主属性对主属性的部分函数依赖,针对我们的例子,分析如下:
主属性:学号,课名
非主属性:姓名,系名,系主任,分数目前只有一张表:
(学号,姓名,系名,系主任,课名,分数)明显,姓名和系名都是对(学号,课名)存在部分函数依赖的。因为其实只需要学号就可以决定姓名和系名。所以这个表目前是不符合第二范式的,我们只好对表作出分解,当然分解的模式不是唯一的,下面只是一种情况,如下所示:
选课(学号,课名,分数)
学生(学号,姓名,系名,系主任)

我们此时再来看两张表是否满足第二范式:
选课表:主属性:(学号,课名)。非主属性:分数。 不存在非主属性对主属性的部分函数依赖,满足第二范式。学生表:主属性:学号。非主属性:系名,系主任,姓名。因为主属性只有一个,所以一定不存在非主属性对主属性的部分函数依赖。满足第二范式。
至于怎么找主属性,不用我强调了吧,要是忘了的话回头看看上面。此时数据变成了这样:
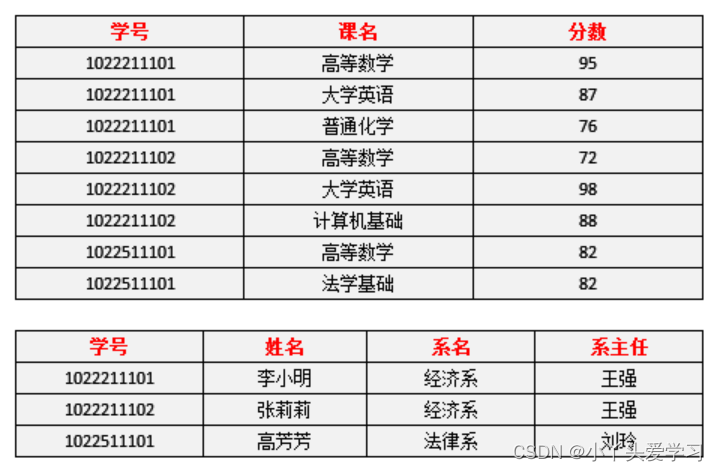
我们回头看看前面的问题有没有得到改善:数据冗余问题:姓名、系名、系主任的数据冗余得到了明显改善。
插入异常问题:现在新开设一个系,尚未招生还是无法将系名插入到学生表中,因为学号是主属性,不能为空。没有改善。
删除异常问题:一个系毕业,删除这个系的所有学生信息,那还是会连带删除掉系的信息。没有改善。因此,只满足第二范式也还是不够。还是存在好多问题。
4.第三范式(3NF)
在第二范式的基础上,确保每列和主键直接相关,而不是间接相关。
在第二范式基础上,消除非主属性对主属性的传递函数依赖,同样,我们继续分析我们的例子:
主属性:学号,课名
非主属性:姓名,系名,系主任,分数目前我们的表如下:
选课(学号,课名,分数)
学生(学号,姓名,系名,系主任)我们发现在学生表中:存在非主属性系主任对主属性学号的传递函数依赖。因为学号->系名,系名->系主任,所以才会出现前面那么多的问题。那我们试着再次分解学生表,消除这种传递函数依赖。分解后如下:
选课(学号,课名,分数)
学生(学号,姓名,系名)
系(系名,系主任)

我们继续分析:
选课表中码为(学号,课名),非主属性为分数,它们是完全函数依赖的关系,不存在非主属性对主属性的传递函数依赖。符合第三范式。
对于学生表,码为学号,主属性为学号,非主属性为系名,不可能存在非主属性对于码的传递函数依赖,符合第三范式,对于系表,码为系名,主属性为系名,非主属性为系主任,不可能存在非主属性对于码的传递函数依赖(至少要有三个属性才可能存在传递函数依赖关系),也符合第三范式。
此时数据成了现在这样:
科目表:
Id name
1 高等数学
2 大学英语

Id 系名 系主任
1 经济系 王强
2 法律系 刘岭Id 学号 姓名
1 1022211101我们再回头看看前面的问题有没有得到改善:
插入异常问题:现在新开设一个系,尚未招生我们却可以保存系的信息,因为我们有系这个表。问题得到改善。
删除异常问题:一个系毕业,删除这个系的所有学生信息,现在不会连带删除掉系的信息,因为我们有系这个表。问题得到改善。
当数据库到达第三范式的时候,基本上有关数据冗余,数据插入、删除、更新的异常问题得到了解决,这也是一个”合法的”数据库最基本的要求,但是效率问题就另当别论了,因为表越多,连接操作就越多,但是连接是一个比较耗资源的操作。对于我们前面的例子,已经优化到最好了,也没有再次优化的地方。下面我们说到BC范式的时候会说另一个例子。
5.练习:
1 请设计数据库
教师表 班级表 学生表 成绩表
MySQL查询语句练习题45题版

-
相关阅读:
C语言判断一个数转二进制的某位是1或者0
2022亚太杯建模B题思路 : 高速列车的优化设计 小美赛数学建模 B题思路
Docker 01 概述
day04-MQ
实践练习命令执行
代理模式-P19
Java 12 及Tomcat 部署配置
R语言dplyr包distinct函数基于dataframe数据中的所有变量移除重复行
vue报错信息汇总
扫地机器人遇冷?科沃斯、石头科技求变
- 原文地址:https://blog.csdn.net/Liu_wen_wen/article/details/125891944