快速排序
每次从当前考虑的数组中选一个元素,把这个元素想办法挪到应该排好序的位置,比如4这个元素,它就有一个性质4之前的元素都是小于它的,之后的元素都是大于它的,之后我们要做的事情是对小于4和大于4的数组分别继续使用快速排序的思路,逐渐递归下去完成整个排序过程。

对于快速排序如果把选定的元素挪到正确的位置的过程也是快速排序的核心,在这个过程中我们通常选择数组第一个元素为我们分界的标志点,我们记录这个点为 l ,之后我们逐渐的遍历右边所有没有被访问的元素,在遍历的过程中我们逐渐整理一部分是小于v这个元素的,一部分是大于v这个元素的,当让我们要有个记录那个是小于v和大于v的分界点,这个点为 j ,而当前访问的元素记录为 i。

我们如何来决定当前的元素要怎样变化才能维持当前的性质,如果当前的元素e是比v还要大的,那么他直接就放在大于v一部分的后面。

然后就考虑下一元素就好了。

如果当前的元素e是比v还要小的。

我们只需要当前橙色部分也就是j所指的位置的后一个元素和当前做考察的元素 i进行一下交换 。

之后我们进行一下位置维护 ++j,++i。

以此类推,整个数组分成三个部分,第一个元素是v,橙色部分小于v,紫色部分大于v。

最后我们需要做的是把数组 l这个位置和数组j这个位置进行交换,这样整个数组就形成了我们设想的那样,前面小于v,后面大于v。

优化
- 对于小规模数组, 使用插入排序进行优化;
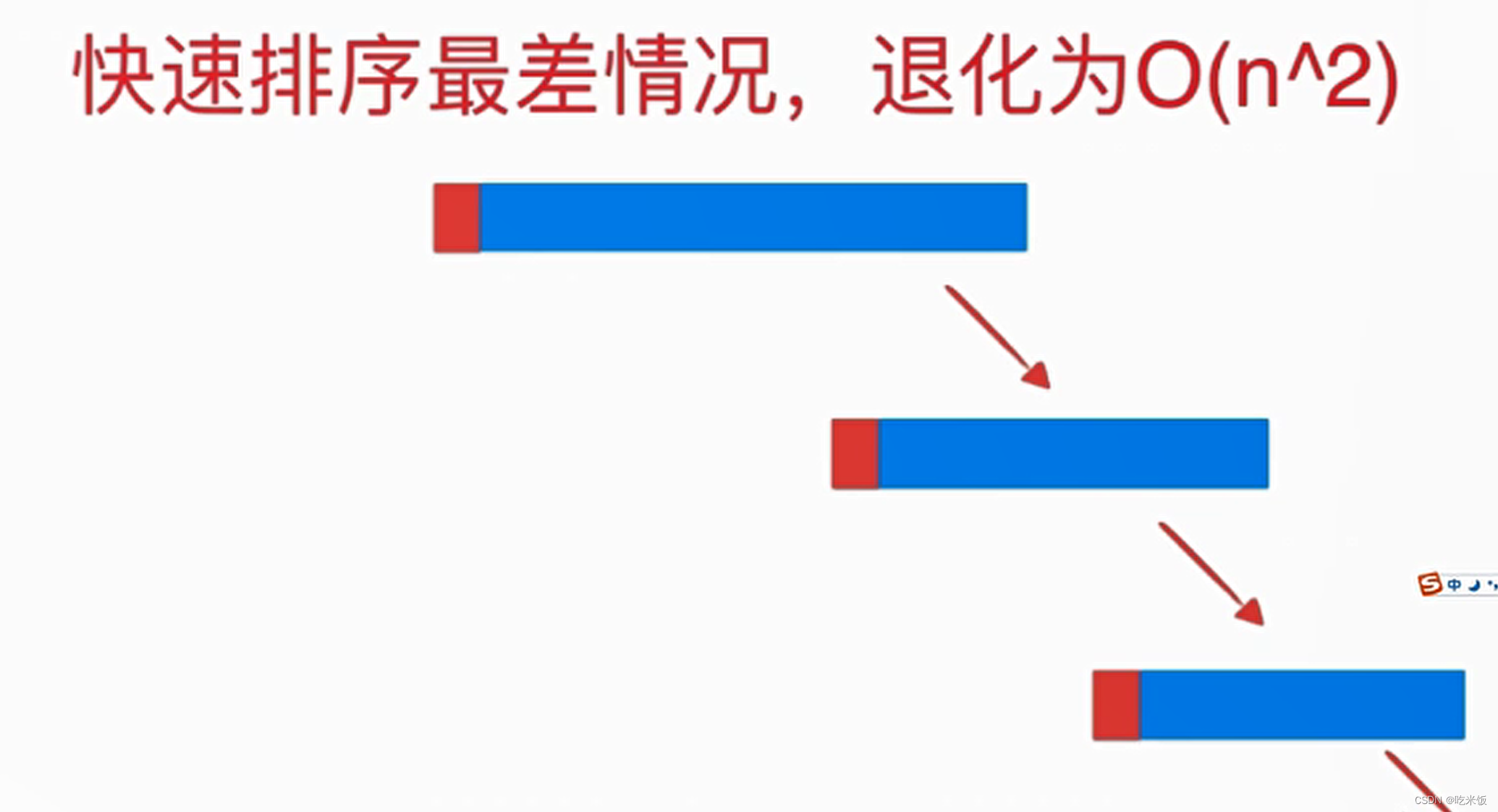
- 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot。在快速排序递归过程中分成的子树不能保证每次都是平均的将整个数组一分为二,换句话来说分成的子数组可能是一大一小的。

- 如果数组近乎或完全有序那么:
quickSort
// 对arr[l...r]范围的数组进行插入排序
template<typename T>
void insertionSort(T arr[], int l, int r) {
for (int i = l + 1; i <= r; ++i) {
T e = arr[i];
int j;
for (j = i; j > l && arr[j - 1] > e; --j) {
arr[j] = arr[j - 1];
}
arr[j] = e;
}
}
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template<typename T>
int __partition1(T arr[], const int l, const int r) {
// 优化:随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
std::swap(arr[l], arr[rand() % (r - l + 1) + l]);
const T v = arr[l];
int j = l;
// arr[l+1...j] < v ; arr[j+1...i) > v
for (int i = l + 1; i <= r; ++i) {
if (arr[i] < v) {
std::swap(arr[++j], arr[i]);
}
}
std::swap(arr[l], arr[j]);
return j;
}
// 对arr[l...r]部分进行快速排序
template<typename T>
void __quickSort(T arr[], const int l, const int r) {
// 优化:对于小规模数组, 使用插入排序进行优化
if (r - l <= 15) {
insertionSort(arr, l, r);
return;
}
const int p = __partition1(arr, l, r);
__quickSort(arr, l, p - 1);
__quickSort(arr, p + 1, r);
}
//快速排序
template<typename T>
void quickSort(T arr[], const int n) {
srand(time(NULL));
__quickSort(arr, 0, n - 1);
}
折叠 双路快速排序
在之前的快速排序我们没有讨论在等于v的情况,在这里无论是把等于放在左边还是右边,如果整个数组出现大量重复的元素,那么它就会造成左右分成的数组极度不平衡从而使算法退化成O(n^2)。
现在呢我们将小于v和大于v放在数组的两端。首先我们从i这个位置开始向后扫描,当我们面对的元素仍然是小于v的时候我们继续向后扫描,知道我们碰到了元素e,它是大于等于v的。

同样 j 亦是如此,

这样话两个绿色的部分就分别归并到橙色和紫色。

而 i和 j这两个所指的元素交换一下位置就可以了。

然后维护一下位置 ++i,--j,以此类推。

quickSort2Ways
// 对arr[l...r]范围的数组进行插入排序
template<typename T>
void insertionSort(T arr[], int l, int r) {
for (int i = l + 1; i <= r; ++i) {
T e = arr[i];
int j;
for (j = i; j > l && arr[j - 1] > e; --j) {
arr[j] = arr[j - 1];
}
arr[j] = e;
}
}
// 双路快速排序的partition
// 返回p, 使得arr[l...p-1] <= arr[p] ; arr[p+1...r] >= arr[p]
// 双路快排处理的元素正好等于arr[p]的时候要注意,详见下面的注释:)
template<typename T>
int __partition2(T arr[], int l, int r) {
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
std::swap(arr[l], arr[rand() % (r - l + 1) + l]);
const T v = arr[l];
// arr[l+1...i) <= v; arr(j...r] >= v
int i = l + 1, j = r;
while (true) {
// 注意这里的边界, arr[i] < v, 不能是arr[i] <= v
// 思考一下为什么?
while (i <= r && arr[i] < v)++i;
// 注意这里的边界, arr[j] > v, 不能是arr[j] >= v
// 思考一下为什么?
while (j >= l + 1 && arr[j] > v)--j;
if (i > j)break;
std::swap(arr[i], arr[j]);
//arr[i] < v. 在碰到很多连续相同数字的情况下,i只向后移动一次,同时j至少向前移动一次,相对平衡。
//arr[i] <= vb, 在碰到很多连续相同数字的情况下, i首先不停向后移动,直到满足条件为止,造成不平衡。
++i;
--j;
}
std::swap(arr[l], arr[j]);
return j;
}
// 对arr[l...r]部分进行快速排序
template<typename T>
void __quickSort2Ways(T arr[], const int l, const int r) {
// 对于小规模数组, 使用插入排序进行优化
if (r - l <= 15) {
insertionSort(arr, l, r);
return;
}
const int p = __partition2(arr, l, r);
__quickSort2Ways(arr, l, p - 1);
__quickSort2Ways(arr, p + 1, r);
}
//快速排序
template<typename T>
void quickSort2Ways(T arr[], const int n) {
srand(time(NULL));
__quickSort2Ways(arr, 0, n - 1);
}
折叠 三路快速排序
之前快速排序的思想都是小于v大于v,而三路快速排序的思想是小于v等于v大于v。在这样分割之后在递归的过程中,对于等于v的我们根本不用管了,只需要递归小于v大于v的部分进行同样的快速排序。

现在我们要处理i位置这个元素e,如果当前元素 e 正好等于v,那么元素e就直接纳入绿色的等于v的部分,相应的 ++i,我们来处理下一位置的元素。

如果当前元素 e 小于v,我们只需要把这个元素和等于v部分的第一个元素进行一次交换就好了。

之后因该维护一下位置,++i,++lt,来查看下一元素。
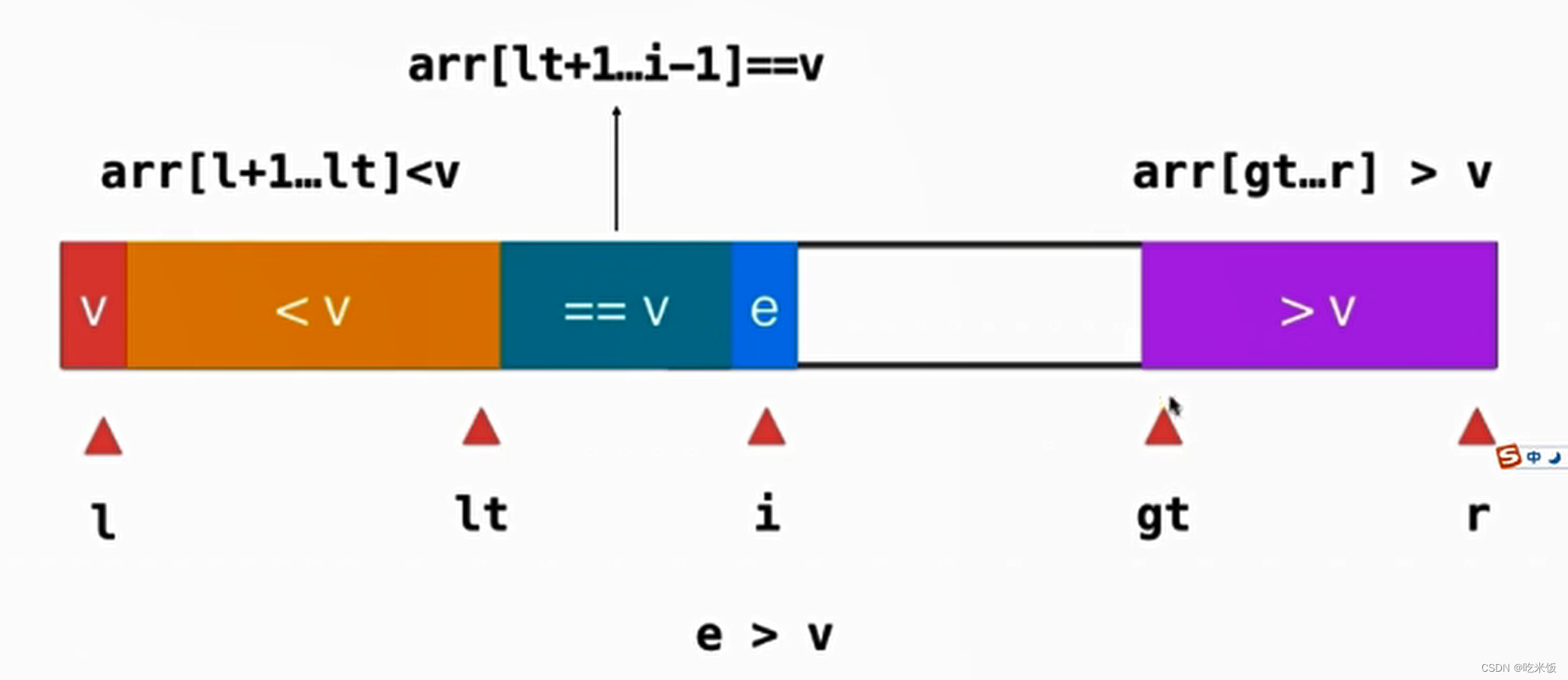
如果当前元素 e 大于v,我们只需要把这个元素和gt-1位置的元素进行一次交换就好了。

相应的我们应该维护一下gt的位置 --gt,需要注意的是i我们不需要动它,因为和它交换的位置元素本就没有讨论过。

以此类推,最后还需要l和lt位置的元素交换一下位置。

此时我们整个数组就变成了这个样子,之后我们只需要对小于v的部分和大于v的部分进行递归的快速排序就好了,至于等于v的部分它已经放在数组合适的位置了。

quickSort3Ways
// 对arr[l...r]范围的数组进行插入排序
template<typename T>
void insertionSort(T arr[], int l, int r) {
for (int i = l + 1; i <= r; ++i) {
T e = arr[i];
int j;
for (j = i; j > l && arr[j - 1] > e; --j) {
arr[j] = arr[j - 1];
}
arr[j] = e;
}
}
// 递归的三路快速排序算法
template<typename T>
void __quickSort3Ways(T arr[], const int l, const int r) {
// 对于小规模数组, 使用插入排序进行优化
if (r - l <= 15) {
insertionSort(arr, l, r);
return;
}
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
std::swap(arr[l], arr[rand() % (r - l + 1) + l]);
T v = arr[l];
int lt = l; // arr[l+1...lt] < v
int gt = r + 1; // arr[gt...r] > v
int i = l + 1; // arr[lt+1...i) == v
while (i < gt) {
if (arr[i] < v) {
std::swap(arr[i], arr[lt + 1]);
++i;
++lt;
} else if (arr[i] > v) {
std::swap(arr[i], arr[gt - 1]);
--gt;
} else { // arr[i] == v
++i;
}
}
std::swap(arr[l], arr[lt]);
__quickSort3Ways(arr, l, lt - 1);
__quickSort3Ways(arr, gt, r);
}
// 对于包含有大量重复数据的数组, 三路快排有巨大的优势
template<typename T>
void quickSort3Ways(T arr[], const int n) {
srand(time(nullptr));
__quickSort3Ways(arr, 0, n - 1);
}
折叠 概述


__EOF__
