简介

$Splay$ 是一种二叉查找树，中文名为伸展树，它通过不断将某个节点旋转到根节点，使得整棵树仍然满足二叉查找树的性质，并且保持平衡而不至于退化为链。它由 $DanielSleator$ 和 $RobertTarjan$ 发明。

前置芝士

• 二叉树
• 平衡二叉搜索树（AVL）

作用

主要思想：对于查找频率较高的节点，使其处于离根节点相对较近的位置上。 保证了查询效率。

实现起来就是，对于每次操作后的节点，执行一次操作：将该节点旋转到根节点。

结构

1. 满足二叉搜索树：左子树任意节点的值 $<$ 根节点的值 $<$ 右子树任意节点的值
2. 节点维护的信息：

Splay的基本操作

写些什么？

rotate

首先要将一个节点旋转到根，需要先考虑如何将一个节点旋转到其父节点。

先来看两种情况：

情况一：

• 当 $x$ 是 $y$ 的左孩子
  

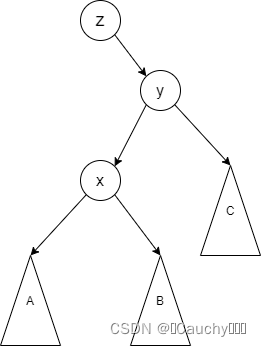
在此处进行 $x$ 右旋到 $y$ 的位置，变动如下：

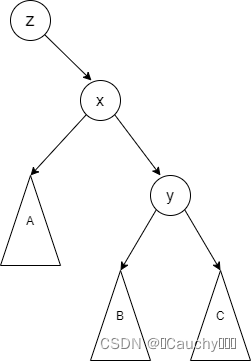
代码实现：

ch[y][0] = ch[x][1], fa[ch[x][1]] = y;
fa[x] = fa[y];
ch[x][1] = y, fa[y] = x;
ch[fa[x]][1] = x;
1
2
3
4

$z$ 的左侧情况对称，不予讨论。

情况二：

• 当 $x$ 是 $y$ 的右孩子
  

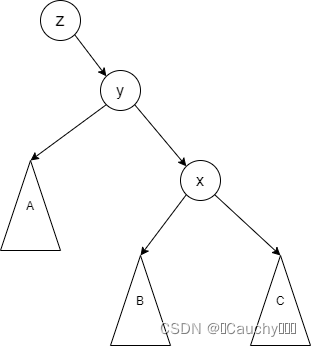
在此处进行 $x$ 左旋到 $y$ 的位置，变动如下：

代码实现：

ch[y][1] = ch[x][0], fa[ch[x][0]] = y;
fa[x] = fa[y];
ch[x][0] = y, fa[y] = x;
ch[fa[x]][1] = x;
1
2
3
4

$z$ 的左侧情况对称，不予讨论。

那么在此统一所有情况，一个函数实现将节点搬至父节点的位置：

• 自行理解，$k$ 表示当前 $x$ 在 $y$ 的哪一侧。

void rotate(int x) {
	int y = fa[x], z = fa[y], k = (x == ch[fa[x]][1]);
	ch[y][k] = ch[x][k ^ 1];
	if(ch[x][k ^ 1]) fa[ch[x][k ^ 1]] = y;
	ch[x][k ^ 1] = y;
	fa[y] = x, fa[x] = z;
	if(z) ch[z][y == ch[z][1]] = x;
}
1
2
3
4
5
6
7
8

---

splay

接下来考虑如何将一个节点旋转至根节点。（拓：旋转至指定父节点之下）

双旋操作

主要分三种情况：

• 第一种： $x$ 的父节点就是根，直接旋一次。

• 第二种：$x$ 和它父节点 $y$ 和它父节点的父节点 $z$ 在一条线上。
  

那么需要先将 $y$ 进行左旋，在将 $x$ 左旋上去。

• 第三种：$x$ 和它父节点 $y$ 和它父节点的父节点 $z$ 不在一条线上。
  

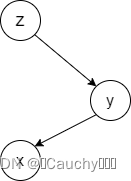
那么对 $x$ 进行一次右旋，在左旋到根。

代码实现：

• 将 $x$ 旋转到根

void splay(int x) {
	while(!fa[x]) {
		int y = fa[x], z = fa[y];
		if(z) rotate(get(x) ^ get(y) ? x : y); // 同侧，先旋y
		rotate(x); // x至少旋一次
	}
	root = x;
}
1
2
3
4
5
6
7
8

• 拓：将 $x$ 旋转到父节点为 $f$，根节点即：$f==0$

void splay(int x, int f) {
	while(fa[x] != f) {
		int y = fa[x], z = fa[y];
		if(z) rotate(get(x) ^ get(y) ? x : y); // 同侧，先旋 y
		rotate(x); // x 至少旋一次
	}
	if(f == 0) root = x;
}
1
2
3
4
5
6
7
8

---

insert

插入操作具体步骤如下（假设插入的值为 $k$ ）：

• 如果树空了，则直接插入根并退出。
• 如果当前节点的权值等于 $k$ 则增加当前节点的大小并更新节点和父亲的信息，将当前节点进行 $splay$ 操作。
• 否则按照二叉查找树的性质向下找，找到空节点就插入即可。（不要忘记 $splay$ 操作）

void insert(int x) {
	if(!root) {
		val[++idx] = x;
		cnt[idx]++;
		root = idx;
		upd(root);
		return ;
	}
	int u = root, f = 0;
	while(1) {
		// 存在
		if(val[u] == x) {
			cnt[u]++;
			upd(u);
			upd(f);
			splay(u, 0);
			break;
		}
		// 向下走
		f = u;
		u = ch[u][val[u] < x]; // 权值小去左侧0
		// 不存在
		if(!u) {
			val[++idx] = x;
			cnt[idx]++;
			fa[idx] = f;
			ch[f][val[f] < x] = idx;
			upd(idx);
			upd(f);
			splay(idx, 0);
			break;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

---

kth

查询排名为 $k$ 的数

• 如果左子树非空，并且剩余排名 $x$ 小于等于左子树的大小 $size$ ，那么向左子树查找。
• 否则将 $k$ 减去左子树和根的大小。如果此时 $k$ 的值小于等于 $0$，则返回根节点的权值，否则继续向右子树查找。

// 查询排名k的数
int kth(int k) {
	int u = root;
	while(1) {
		// 存在左子树，小于左子树大小，去左子树
		if(ch[u][0] && k <= sz[ch[u][0]]) u = ch[u][0];
		else {
			// 否则先减去当前和左子树大小，cnt，sz
			k -= cnt[u] + sz[ch[u][0]];
			// 找到当前节点
			if(k <= 0) { splay(u, 0); return val[u]; }
			// 去右子树
			u = ch[u][1];
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

---

rk

查询值为 $k$ 的排名大小，依据二叉搜索树性质。

• 如果 $k$ 比当前节点的权值小，向其左子树查找。
• 如果 $k$ 比当前节点的权值大，将答案加上左子树（$size$）和当前节点（cnt）的大小，向其右子树查找。
• 如果 $k$ 与当前节点的权值相同，将答案加 $1$ 并返回。

// 查询k的排名
int rk(int k) {
	int res = 0, u = root;
	while(1) {
		// 更小去左子树
		if(k < val[u]) u = ch[u][0];
		else {
			// 否则先加上左子树个数
			res += sz[ch[u][0]];
			// 相等 + 1
			if(k == val[u]) { splay(u, 0); return res + 1; }
			// 加上当前个数，cnt
			res += cnt[u];
			// 去右子树
			u = ch[u][1];
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

---

pre

查找前驱

// 查找前驱
int pre() {
	int u = ch[root][0];
	if(!u) return u;
	while(ch[u][1]) u = ch[u][1];
	splay(u, 0);
	return u;
}
1
2
3
4
5
6
7
8

---

nxt

查找后继

// 查后继
int nxt() {
	int u = ch[root][1];
	if(!u) return u;
	while(ch[u][0]) u = ch[u][0];
	splay(u, 0);
	return u;
}
1
2
3
4
5
6
7
8

---

del

合并两棵 Splay 树

设两棵树的根节点分别为 $x$ 和 $y$ ，那么我们要求 $x$ 树中的最大值小于 $y$ 树中的最小值。合并操作如下：

• 如果 $x$ 和 $y$ 其中之一或两者都为空树，直接返回不为空的那一棵树的根节点或空树。
• 否则将 $x$ 树中的最大值 $splay$ 到根，然后把它的右子树设置为 $y$ 并更新节点的信息，然后返回这个节点。

删除操作：

首先将 $x$ 旋转到根的位置。

• 如果 $cnt[x]>1$（有不止一个 ），那么将 $cnt[x]>1$ 减 $1$ 并退出。
• 否则，合并它的左右两棵子树即可。

void del(int k) {
	rk(k); // 先将k旋到根
	if(cnt[root] > 1) { cnt[root]--; upd(root); return ;}
	// 合并它的左右两棵子树
	if(!ch[root][0] && !ch[root][1]) { clear(root); root = 0; return ;}
	if(!ch[root][0]) {
		int u = root;
		root = ch[root][1];
		fa[root] = 0;
		clear(u);
		return ;
	}
	if(!ch[root][1]) {
		int u = root;
		root = ch[root][0];
		fa[root] = 0;
		clear(u);
		return ;
	}
	int u = root, x = pre();
	fa[ch[u][1]] = x;
	ch[x][1] = ch[u][1];
	clear(u);
	upd(root);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

upd、get、clear

// 更新节点信息
void upd(int x) { sz[x] = sz[ch[x][0]] + sz[ch[x][1]] + cnt[x]; }
// 判断是父节点的左右孩子
int get(int x) { return x == ch[fa[x]][1]; }
// 清除节点信息
void clear(int x) { ch[x][0] = ch[x][1] = fa[x] = val[x] = sz[x] = cnt[x] = 0; }

1
2
3
4
5
6
7

---

题目

P3369 【模板】普通平衡树

题目描述

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;

int idx, root;
int fa[N], ch[N][2], sz[N], cnt[N], val[N];

struct Splay {

void upd(int x) { sz[x] = sz[ch[x][0]] + sz[ch[x][1]] + cnt[x]; }

int get(int x) { return x == ch[fa[x]][1]; }

void clear(int x) { ch[x][0] = ch[x][1] = fa[x] = val[x] = sz[x] = cnt[x] = 0; }

void rotate(int x) {
	int y = fa[x], z = fa[y], k = get(x);
	ch[y][k] = ch[x][k ^ 1];
	if(ch[x][k ^ 1]) fa[ch[x][k ^ 1]] = y;
	ch[x][k ^ 1] = y;
	fa[y] = x, fa[x] = z;
	if(z) ch[z][y == ch[z][1]] = x; // fa[y] 变了，不能get(y)
	upd(y), upd(x);
}

// 把一个点双旋到根，可以使得从根到它的路径上的所有点的深度变为大约原来的一半，其它点的深度最多增加2
void splay(int x, int f) {
	while(fa[x] != f) {
		int y = fa[x], z = fa[y];
		if(z) rotate(get(x) ^ get(y) ? x : y); // 同侧，先旋y
		rotate(x); // x至少旋一次
	}
	if(f == 0) root = x;
}

void insert(int x) {
	if(!root) {
		val[++idx] = x;
		cnt[idx]++;
		root = idx;
		upd(root);
		return ;
	}
	int u = root, f = 0;
	while(1) {
		// 存在
		if(val[u] == x) {
			cnt[u]++;
			upd(u);
			upd(f);
			splay(u, 0);
			break;
		}
		// 向下走
		f = u;
		u = ch[u][val[u] < x]; // 权值小去左侧0
		// 不存在
		if(!u) {
			val[++idx] = x;
			cnt[idx]++;
			fa[idx] = f;
			ch[f][val[f] < x] = idx;
			upd(idx);
			upd(f);
			splay(idx, 0);
			break;
		}
	}
}


void del(int k) {
	rk(k); // 先将k旋到根
	if(cnt[root] > 1) { cnt[root]--; upd(root); return ;}
	// 合并它的左右两棵子树
	if(!ch[root][0] && !ch[root][1]) { clear(root); root = 0; return ;}
	if(!ch[root][0]) {
		int u = root;
		root = ch[root][1];
		fa[root] = 0;
		clear(u);
		return ;
	}
	if(!ch[root][1]) {
		int u = root;
		root = ch[root][0];
		fa[root] = 0;
		clear(u);
		return ;
	}
	int u = root, x = pre();
	fa[ch[u][1]] = x;
	ch[x][1] = ch[u][1];
	clear(u);
	upd(root);
}

// 查询k的排名
int rk(int k) {
	int res = 0, u = root;
	while(1) {
		// 更小去左子树
		if(k < val[u]) u = ch[u][0];
		else {
			// 否则先加上左子树个数
			res += sz[ch[u][0]];
			// 相等 + 1
			if(k == val[u]) { splay(u, 0); return res + 1; }
			// 加上当前个数，cnt
			res += cnt[u];
			// 去右子树
			u = ch[u][1];
		}
	}
}

// 查询排名k的数
int kth(int k) {
	int u = root;
	while(1) {
		// 存在左子树，小于左子树大小，去左子树
		if(ch[u][0] && k <= sz[ch[u][0]]) u = ch[u][0];
		else {
			// 否则先减去当前和左子树大小，cnt，sz
			k -= cnt[u] + sz[ch[u][0]];
			// 找到当前节点
			if(k <= 0) { splay(u, 0); return val[u]; }
			// 去右子树
			u = ch[u][1];
		}
	}
}

// 查找前驱
int pre() {
	int u = ch[root][0];
	if(!u) return u;
	while(ch[u][1]) u = ch[u][1];
	splay(u, 0);
	return u;
}

// 查后继
int nxt() {
	int u = ch[root][1];
	if(!u) return u;
	while(ch[u][0]) u = ch[u][0];
	splay(u, 0);
	return u;
}

};

int main() {
	int n; scanf("%d", &n);
	Splay s;
	while(n--) {
		int x, y;
		scanf("%d%d", &x, &y);
		if(x == 1) {
			s.insert(y);
		} else if(x == 2) {
			s.del(y);
		} else if(x == 3) {
			printf("%d\n", s.rk(y));
		} else if(x == 4) {
			printf("%d\n", s.kth(y));
		} else if(x == 5) {
			s.insert(y);
			printf("%d\n", val[s.pre()]);
			s.del(y);
		} else {
			s.insert(y);
			printf("%d\n", val[s.nxt()]);
			s.del(y);
		}
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180

---