应用

这里的最小环和spfa求负环不一样，这里是没有负环的，就是找一个环是最小值

原理

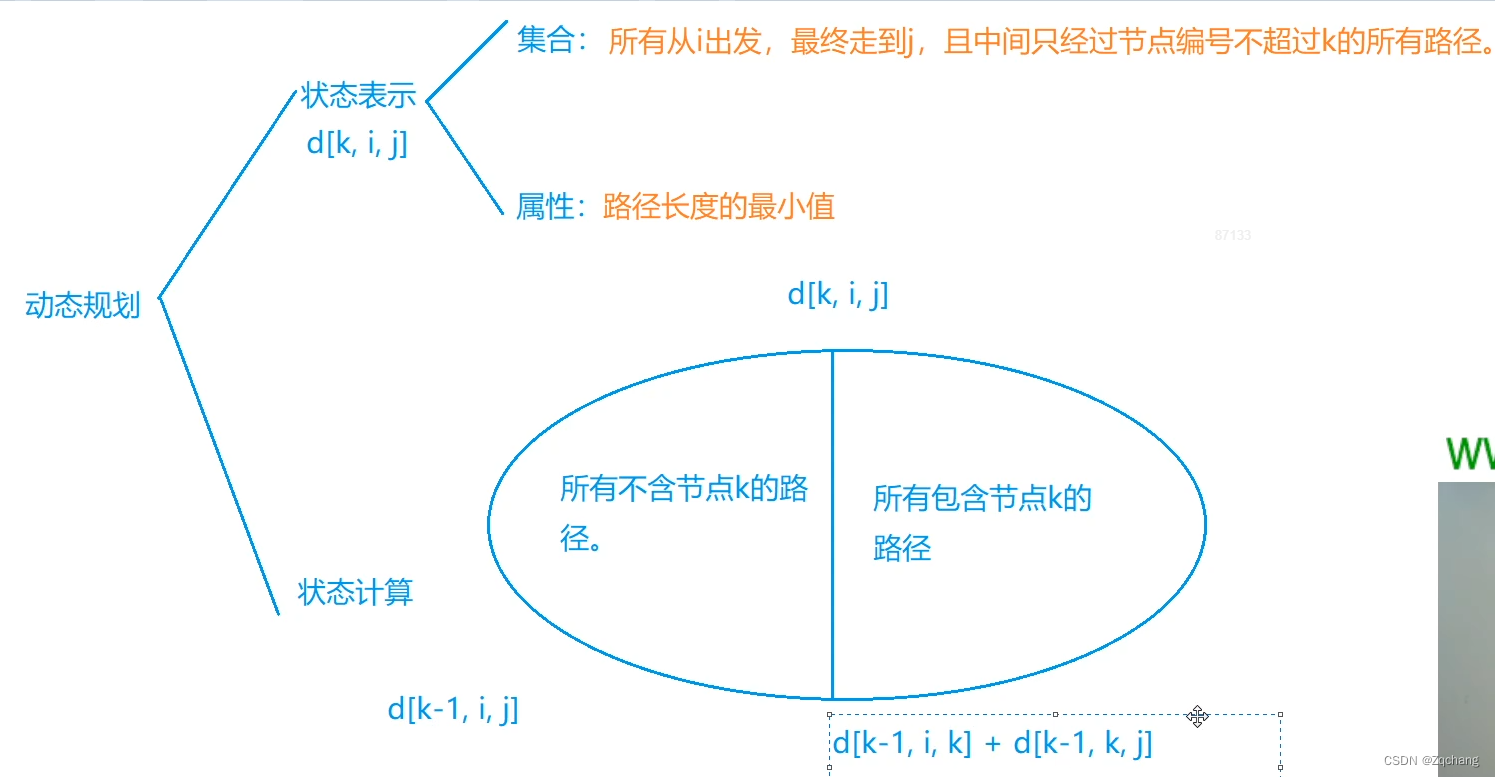
这两个一样，第一维可以直接去掉
证明：当i=k或者j=k的时候，d[i][k]或者d[k][j]是不会更新的，也就是d[k][i][k]等于d[k-1][i][k]，j同理，也就是更新的时候，d[i][k]和d[k][j]不用担心被更新过，当然就可以直接用来更新，不用担心有什么变化

例题

最短路

牛的旅行
其实就是给你一堆连通块，让你加边，使得连通块成为 一个大的连通块

让你求这个大的连通块中两点之间最大值的最小值

分为两种情况，也就是途中两种，一种是原本连通块中的最大值，另一个是经过新边的最长路径

做法如下

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define PII pair<int, int>
#define x first
#define y second
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
const int N = 155;
const double INF = 1e20;
int n;
PII q[N];
double d[N][N];
double maxd[N];
char g[N][N];

double get_dist(PII a, PII b)
{
	double dx = a.x - b.x;
	double dy = a.y - b.y;
	
	return sqrt(dx * dx + dy * dy);
}

signed main()
{
	fast;
	cin >> n;
	for(int i=0; i<n; i++) cin >> q[i].x >> q[i].y;
	
	for(int i=0; i<n; i++) cin >> g[i];
	
	for(int i=0; i<n; i++) 
		for(int j=0; j<n; j++)
		{
			if(i == j) d[i][j] = 0;
			else if(g[i][j] == '0') d[i][j] = INF;
			else d[i][j] = get_dist(q[i], q[j]);
		}
	
	for(int k=0; k<n; k++)
		for(int i=0; i<n; i++)
			for(int j=0; j<n; j++)
				d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

	double res1 = 0;
	for(int i=0; i<n; i++)
	{
		for(int j=0; j<n; j++)
			if(d[i][j] < INF / 2)
				maxd[i] = max(maxd[i], d[i][j]);
		res1 = max(res1, maxd[i]);
	}
		
	double res2 = INF;	
	for(int i=0; i<n; i++)
		for(int j=0; j<n; j++)
			if(d[i][j] > INF / 2)
				res2 = min(res2, maxd[i] + get_dist(q[i], q[j]) + maxd[j]);

	printf("%.6lf\n", max(res1, res2));
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

传递闭包

传递闭包：把所有间接能到的点，都连上边之后，就是一个原图的传递闭包（详见离散）

fioyd算法可以在O($n^3$)的复杂度之内，求出来原图的一个传递闭包，用邻接矩阵的形式表示的

很好做，就是给你一个邻接矩阵g[i][j]，然后初始化，方式如图，然后三层循环，如果i能到k，k能到j，就让d[i][j] = 1