牛顿迭代法

牛顿迭代法

介绍

牛顿法是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。牛顿法常用来求解非线程方程近似根。牛顿法通过迭代的方式去逼近方程的解。

原理

如图所示，牛顿法通过迭代的方式去逼近方程的解，通过利用初始点的斜率去逼近方程的根。而点的斜率公式又可以通过方程的导数得出。我们在(x0,f(x0))斜率做斜线f'(x0)，求出与X轴的交点x1，重复以上过程直到f(xn)无限接近于0即可。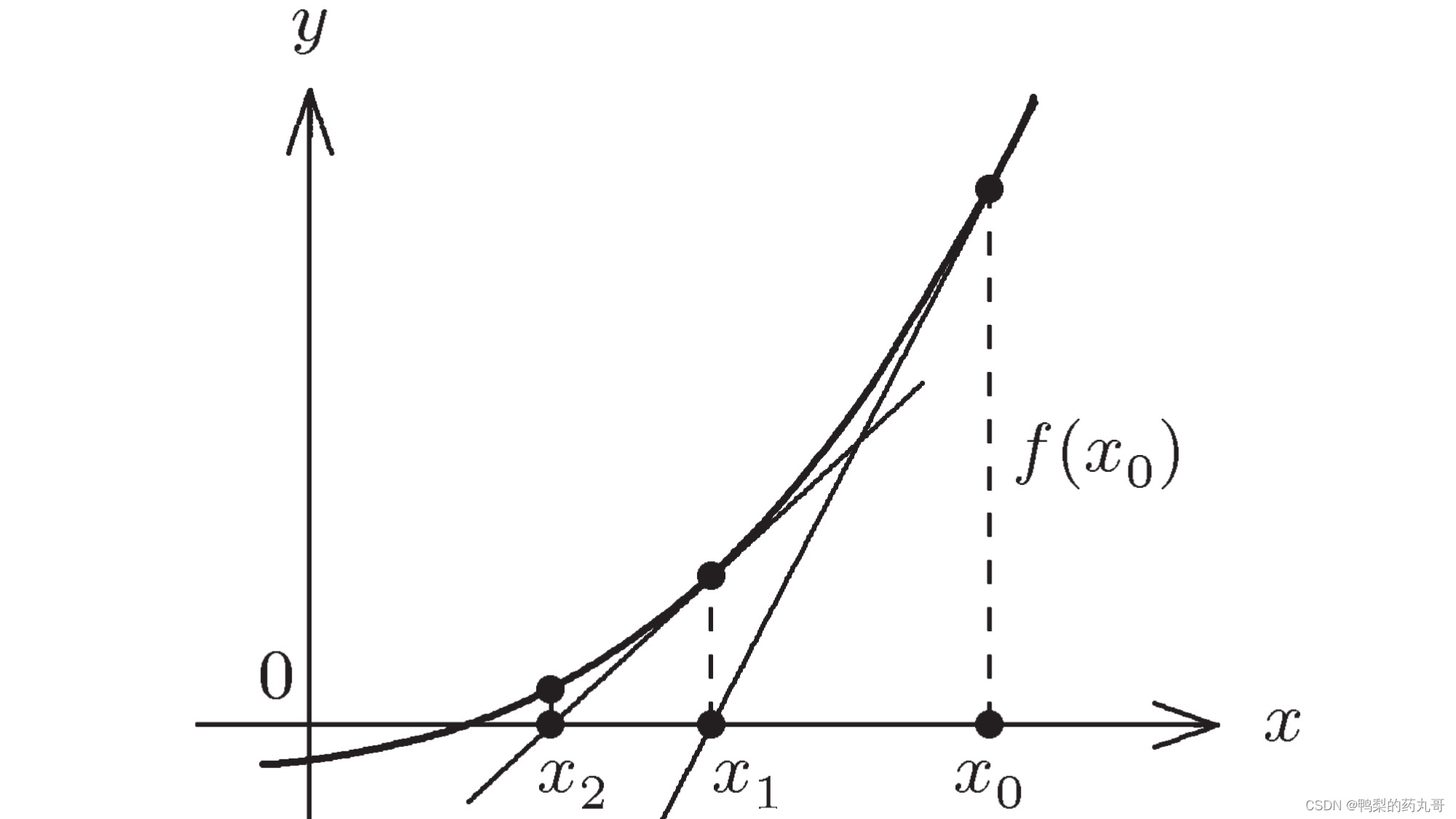

​

​ 设有一非线性方程f(x)，为了求该方程的根，可以设一个初始值x0，设该点的斜率方程为f'(x0)，那么f'(x0)和X轴有交点x1。那么，可以得出x1=x0-f(x0)/f'(x0)。求出x1后就继续求x2，x3。直至f(xn)接近于0，当然也可以用两个点xn和xn-1之间的差接近于0来代表迭代的结束；于是有以下公式：
$$x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}$$

例题

leetcode第69题.x的平方根

69. x 的平方根 - 力扣（LeetCode）

如题：

解题思路：

x 的平方根 - x 的平方根 - 力扣（LeetCode）

注意题目不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 ，去求要求的数的平方根

在解题中设待求平方根的数为C，那么求平方根的公式为
$$f(x)=x^2-C$$
然后根据上面的牛顿迭代公式：
$$x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}$$
可以得出：
$$x_{i+1}=\frac{1}{2}\left(x_i+\frac{C}{x_i}\right)$$
然后题目设x0=C为初始值
$$x_0=C$$
通过迭代去逼近方程中的其中的一个解，即是C的平方根
$$x=\sqrt{C}$$