搜素专题（DFS ）

前言

 搜素是一种暴力的方法
 可以按照树去理解
 在不剪支的情况下，可以把所有 *方案* “枚举”出来
 剪支 --> 在确定一定不会是解的情况下，提前终止该"点"下面的搜素
1
2
3
4

类似树结构进行

---

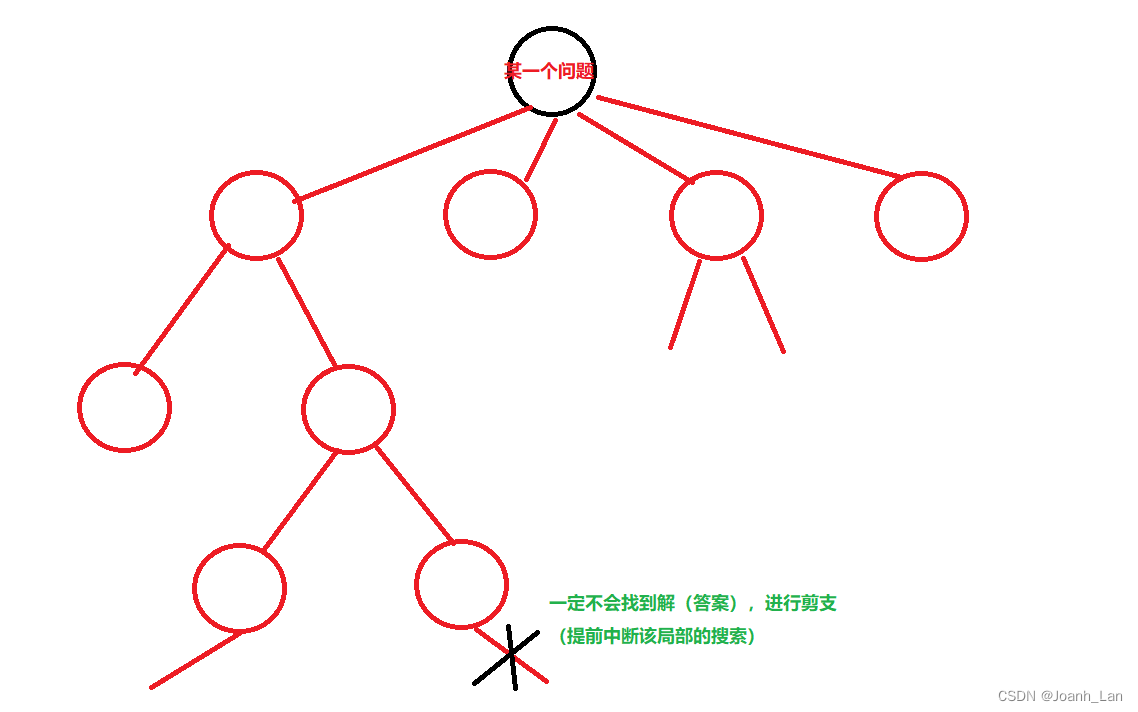
一个问题可以被拆分成几个子部分去解决（有点DP的味道了，但本节课只是简单的搜索，方向食用）

换成人话来说：

如果把问题抽象成集合，每一个元素都可以看成一个局部的方案

所有 由一个个元素构成的子集 都可能会是问题的一个解

如果还有点晕

来一个实际的问题助助兴吧

123 这三个数全排列

图上每一个集合，都是问题的一个解

如：3 1 2

---

全排列实现代码

#include <bits/stdc++.h>
#define buff                     \
    ios::sync_with_stdio(false); \
    cin.tie(0);
//#define int long long
using namespace std;
const int N = 1000;
bool st[N];
int ans[N];
int n;
void dfs(int cnt)
{
    if (cnt == n)
    {
        for (int i = 1; i <= n; i++)
        {
            cout << ans[i];
            cout << (i == n ? '\n' : ' ');
        }
    }
    for (int i = 1; i <= n; i++)
    {
        if (!st[i])
        {
            ans[cnt + 1] = i;
            st[i] = 1;
            dfs(cnt + 1);
            st[i] = 0;
        }
    }
}
void solve()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        ans[1] = i;
        st[i] = 1;
        dfs(1);
        st[i] = 0;
    }
}
int main()
{
    solve();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

模板

void dfs(需要使用的参数)
{
    if(满足题意的条件)
    {
        xxx
    }

    if(边界条件 | 剪支)
    {
        xxx
        return 
    }

    灵活的dfs过程
    根据题意书写，很灵活！
    怎么舒服怎么来 (:

    for (条件)
    {
        xxx
        xxx
        st[idx] = 1;//****
        dfs(xxx)
        st[idx] = 0//****
    }
    
    or

    dfs(xxx)

    等等

    cout << ans << '\n';
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

题目

P2392 kkksc03考前临时抱佛脚

https://www.luogu.com.cn/problem/P2392

AC代码

#include <bits/stdc++.h>
#define buff                     \
    ios::sync_with_stdio(false); \
    cin.tie(0);
//#define int long long
using namespace std;
const int N = 1000;

int a[N];
int n1, n2, n3, n4;
int ans = 0, tt = 0;
int nn;
void dfs(int l, int r, int cnt)
{
    if (cnt == nn)
    {
        tt = min(tt,max(l, r));
        return;
    }
        dfs(l + a[cnt + 1], r, cnt + 1);
        dfs(l, r + a[cnt + 1], cnt + 1);
}
void solve()
{
    cin >> n1 >> n2 >> n3 >> n4;

    for (int i = 1; i <= n1; i++)
        cin >> a[i];
    nn = n1, tt = 0x3f3f3f3f;
    dfs(0, 0, 0);
    ans += tt;

    for (int i = 1; i <= n2; i++)
        cin >> a[i];
    nn = n2, tt = 0x3f3f3f3f;
    dfs(0, 0, 0);
    ans += tt;


    for (int i = 1; i <= n3; i++)
        cin >> a[i];
    nn = n3, tt = 0x3f3f3f3f;
    dfs(0, 0, 0);
    ans += tt;

    for (int i = 1; i <= n4; i++)
        cin >> a[i];
    nn = n4, tt = 0x3f3f3f3f;
    dfs(0, 0, 0);
    ans += tt;

    cout << ans << endl;
}
int main()
{
    solve();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

P1135 奇怪的电梯

https://www.luogu.com.cn/problem/P1135

T代码

---

太过暴力，没有处理好重复的局部方案

换句话来说：剪支处理不到位

---

#include <bits/stdc++.h>
#define buff                     \
    ios::sync_with_stdio(false); \
    cin.tie(0);
//#define int long long
using namespace std;
const int N = 1000;
int s[N];
int n, bg, ed;
int ans = 0x3f3f3f3f;

void dfs(int idx, int cnt)
{
    if (idx <= 0 || cnt > n)
        return ;
    if (idx == ed)
    {
        ans = min(ans, cnt);
        return ;
    }
    dfs(idx + s[idx],cnt + 1);
    dfs(idx - s[idx],cnt + 1);
}

void solve()
{
    cin >> n >> bg >> ed;

    for (int i = 1; i <= n; i++)
        cin >> s[i];

    dfs(bg,0);

    cout << (ans == 0x3f3f3f3f ? -1 : ans) << '\n';
}
int main()
{
    solve();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

AC代码

#include <bits/stdc++.h>
#define buff                     \
    ios::sync_with_stdio(false); \
    cin.tie(0);
//#define int long long
using namespace std;
const int N = 1000;
int s[N];
int n, bg, ed;
int ans = 0x3f3f3f3f;
bool st[N];
void dfs(int idx, int cnt)
{
    if (idx <= 0 || cnt > n || st[idx] || idx > n || cnt >= ans)
        return ;
    if (idx == ed)
    {
        ans = min(ans, cnt);
        return ;
    }
    st[idx] = 1;
    dfs(idx + s[idx],cnt + 1);
    dfs(idx - s[idx],cnt + 1);
    st[idx] = 0;
}

void solve()
{
    cin >> n >> bg >> ed;

    for (int i = 1; i <= n; i++)
        cin >> s[i];

    dfs(bg,0);

    cout << (ans == 0x3f3f3f3f ? -1 : ans) << '\n';
}
int main()
{
    solve();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

本题の总结

1.标记的正确使用
2.剪支的判断 & 优化
...
1
2
3

计数类

P1605 迷宫

https://www.luogu.com.cn/problem/P1605

AC代码

#include <bits/stdc++.h>
#define buff                     \
    ios::sync_with_stdio(false); \
    cin.tie(0);
//#define int long long
using namespace std;
const int N = 1000;
int n, m, t;
int bgx, bgy, edx, edy;
int s[N][N];
bool st[N][N];
int xx[4] = {0, 1, -1, 0}, yy[4] = {1, 0, 0, -1};
int ans;
void dfs(int x, int y)
{
    if (x == edx && y == edy)
    {
        ans++;
        return;
    }

    for (int i = 0; i < 4; i++)
    {
        int tx = x + xx[i], ty = y + yy[i];

        if ((tx >= 1 && tx <= n) && (ty >= 1 && ty <= m) && !s[tx][ty] && !st[tx][ty])
        {
            st[x][y] = 1;
            dfs(tx, ty);
            st[x][y] = 0;
        }
    }
}
void solve()
{
    cin >> n >> m >> t;

    cin >> bgx >> bgy >> edx >> edy;
    for (int i = 1; i <= t; i++)
    {
        int a, b;
        cin >> a >> b;
        s[a][b] = 1;
    }
    dfs(bgx, bgy);

    cout << ans << endl;
}
int main()
{
    solve();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52