AcWing 1072. 树的最长路径

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说，要找到一条路径，使得使得路径两端的点的距离最远。
注意：路径中可以只包含一个点。

解题思路

这是树型DP的第一类题型
并没有类似于DP中的表达式，而是借用DP的思想进行解题
使用dfs，从任意一点开始都可，函数中标记父节点保证遍历方向正确，同时记录d1和d2
其中d1为当前节点的最长距离，d2为当前节点的次长距离，那么最长路径就是d1+d2，用ans记录一个最大值
同时dist变量返回当前搜索中的最长距离，并在回溯时被上一层dfs使用

AC代码

/****************
 *@description:for the Escape Project
 *@author: Nebula_xuan
 * @Date: 2022-07-04 16:58:16
 *************************************************************************/

#include <iostream>
#include <cstring>
using namespace std;
const int N = 2e4 + 10;
int e[N], ne[N], h[N], idx, w[N], r[N];
long long f[N];
int ans = 0;
void add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
int dfs(int u, int fa)
{
    int dist = 0, d1 = 0, d2 = 0;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (j == fa)
            continue;
        int t = dfs(j, u) + w[i];
        dist = max(t, dist);
        if (t > d1)
        {
            d2 = d1;
            d1 = t;
        }
        else if (t > d2)
            d2 = t;
    }
    ans = max(ans, d1 + d2);
    return dist;
}
int main()
{
    int n;
    cin >> n;
    memset(h, -1, sizeof h);
    for (int i = 1; i < n; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
        add(b, a, c);
    }
    dfs(1, -1);
    cout << ans << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

AcWing 1073. 树的中心

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。
请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。

解题思路

使用两边dfs
第一遍从叶子节点向上遍历
找到每个点向下走的最大值和次大值
第二遍dfs
我们找它指向根节点的最大值
此时我们从根节点开始向下遍历
如果当前节点的子节点的最大距离等于父节点的最大距离加上他们之间的距离，那么它向上走的最远距离就是它的次大距离加上它们之间的距离
否则向上的最大距离就是父节点的最大距离加上它们之间的距离，此时我们寻找当前节点向下走和向上走的最大值，取最小值就是答案

AC代码

/****************
 *@description:for the Escape Project
 *@author: Nebula_xuan
 * @Date: 2022-07-04 17:27:50
 *************************************************************************/

#include <iostream>
#include <cstring>
using namespace std;
const int N = 2e4 + 10;
int e[N], ne[N], w[N], idx, h[N];
int f[N][3];
void add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
void dfs1(int u, int fa)
{
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int v = e[i];
        if (v == fa)
            continue;
        dfs1(v, u);
        if (f[v][0] + w[i] >= f[u][0])
        {
            f[u][1] = f[u][0];
            f[u][0] = f[v][0] + w[i];
        }
        else if (f[v][0] + w[i] > f[u][1])
        {
            f[u][1] = f[v][0] + w[i];
        }
    }
}
void dfs2(int u, int fa)
{
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int v = e[i];
        if (v == fa)
            continue;
        int t = -1;
        if (f[u][0] == f[v][0] + w[i])
            t = max(f[u][2], f[u][1]);
        else
            t = max(f[u][0], f[u][2]);
        if (t >= 0)
            f[v][2] = t + w[i];
        dfs2(v, u);
    }
}
int main()
{
    int t;
    cin >> t;
    memset(h, -1, sizeof h);
    for (int i = 1; i < t; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
        add(b, a, c);
    }
    dfs1(1, -1);
    dfs2(1, -1);
    int maxx = 1e9 + 10;
    for (int i = 1; i <= t; i++)
        maxx = min(maxx, max(f[i][0], f[i][2]));
    cout << maxx;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

1075. 数字转换

如果一个数 x 的约数之和 y（不包括他本身）比他本身小，那么 x 可以变成 y，y 也可以变成 x。

例如，4 可以变为 3，1 可以变为 7。

限定所有数字变换在不超过 n 的正整数范围内进行，求不断进行数字变换且不出现重复数字的最多变换步数。

解题思路

题目要求约数之和比本身小才能进行相互转化
那么我们将约数之和到它本身建一条有向边，然后我们从小到大进行dfs
很容易想到从未被遍历到的最小约数之和往上进行遍历的答案必然比该路径中途向上遍历的答案大，所以我们可以用vis数组寻找未被遍历过的值不断向上进行dfs，求最大值
具体求法类似于《树的最长路径》

AC代码

/****************
 *@description:for the Escape Project
 *@author: Nebula_xuan
 * @Date: 2022-07-05 09:31:35
 *************************************************************************/

#include <iostream>
#include <cstring>
using namespace std;
const int N = 5e4 + 10;
const int M = 1e5 + 10;
int f[N];
int e[M], ne[M], idx, h[M];
int vis[N];
int ans = 0;
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dfs(int u)
{
    vis[u] = 1;
    int d1 = 0, d2 = 0, dist = 0;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int v = e[i];
        if (!vis[v])
        {
            int t = dfs(v);
            dist = max(dist, t);
            if (t >= d1)
            {
                d2 = d1;
                d1 = t;
            }
            else if (t > d2)
                d2 =t;
        }
    }
    ans = max(d1 + d2, ans);
    return dist + 1;
}
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 2; j * i <= n; j++)
        {
            f[i * j] += i;
        }
    }
    memset(h, -1, sizeof h);
    for (int i = 2; i <= n; i++)
    {
        if (f[i] < i)
            add(f[i], i);
    }
    for (int i = 1; i <= n; i++)
        if (!vis[i])
            dfs(i);
    cout << ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

1074. 二叉苹果树

有一棵二叉苹果树，如果树枝有分叉，一定是分两叉，即没有只有一个儿子的节点。
这棵树共 N 个节点，编号为 1 至 N，树根编号一定为 1。
我们用一根树枝两端连接的节点编号描述一根树枝的位置。
一棵苹果树的树枝太多了，需要剪枝。但是一些树枝上长有苹果，给定需要保留的树枝数量，求最多能留住多少苹果。
这里的保留是指最终与1号点连通。

解题思路

这是另一类树型DP题
已知树根为1，那么我们直接从1开始向下遍历到叶子节点
然后再往上遍历
接着就是很简单的背包问题了

AC代码

/****************
 *@description:for the Escape Project
 *@author: Nebula_xuan
 * @Date: 2022-07-05 10:19:25
 *************************************************************************/

#include <iostream>
#include <cstring>
using namespace std;
const int N = 110;
int f[N][N];
const int M = 2 * N;
int e[M], ne[M], idx, w[M], h[M];
int n, m;
void add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
void dfs(int u, int fa)
{
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int v = e[i];
        if (v == fa)
            continue;
        dfs(v, u);
        for (int j = m; j>=1; j--)
        {
            for (int k = 0; k <= j - 1; k++)
                f[u][j] = max(f[u][j], f[u][j - k - 1] + f[v][k] + w[i]);
        }
    }
}
int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for (int i = 1; i < n; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
        add(b, a, c);
    }
    dfs(1, -1);
    cout << f[1][m];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

323. 战略游戏

鲍勃喜欢玩电脑游戏，特别是战略游戏，但有时他找不到解决问题的方法，这让他很伤心。

现在他有以下问题。

他必须保护一座中世纪城市，这条城市的道路构成了一棵树。

每个节点上的士兵可以观察到所有和这个点相连的边。

他必须在节点上放置最少数量的士兵，以便他们可以观察到所有的边。

你能帮助他吗？

例如，下面的树：

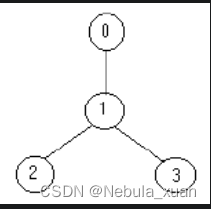
只需要放置 1 名士兵（在节点 1 处），就可观察到所有的边。

解题思路

本题是在节点上放士兵观察边
那么只有两种情况
1.子节点放置了士兵，那么父节点可放可不放
2.子节点未放置士兵，那么父节点必须要放

记得初始化当前节点放置士兵和不放置士兵的值
注意寻找度只有1的根节点从遍历

AC代码

/****************
 *@description:for the Escape Project
 *@author: Nebula_xuan
 * @Date: 2022-07-05 10:31:46
 *************************************************************************/

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1510;
int e[N], ne[N], h[N], idx;
int f[N][2];
int n;
bool vis[N];
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u)
{
    f[u][0] = 0;
    f[u][1] = 1;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int v = e[i];
        dfs(v);
        f[u][1] += min(f[v][0], f[v][1]);
        f[u][0] += f[v][1];
    }
}
int main()
{
    while (cin >> n)
    {
        idx = 0;
        memset(h, -1, sizeof h);
        memset(f, 0, sizeof f);
        memset(vis, 0, sizeof vis);
        for (int i = 0; i < n; i++)
        {
            int x, t;
            scanf("%d:(%d)", &x, &t);
            while (t--)
            {
                int y;
                cin >> y;
                add(x, y);
                vis[y] = 1;
            }
        }
        int root = 0;
        while (vis[root])
            root++;
        dfs(root);
        if (f[root][0] == 0)
            cout << f[root][1] << endl;
        else
            cout << min(f[root][0], f[root][1]) << endl;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

1077. 皇宫看守

太平王世子事件后，陆小凤成了皇上特聘的御前一品侍卫。
皇宫各个宫殿的分布，呈一棵树的形状，宫殿可视为树中结点，两个宫殿之间如果存在道路直接相连，则该道路视为树中的一条边。
已知，在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况，还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。
大内保卫森严，三步一岗，五步一哨，每个宫殿都要有人全天候看守，在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足，无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫，在看守全部宫殿的前提下，使得花费的经费最少。

解题思路

本题和上题不同的地方在于节点需要观察的是相邻的结点，而不是临边
那么情况考虑就会不一样了
父节点 放置 哨兵，所有子节点都 可放可不放 哨兵
父节点 不放 哨兵，但是他至少有一个 子节点 放置哨兵，观察住了他
父节点 不放 哨兵，但 父节点 的 父节点 放置哨兵观察，则 子节点 可放可不放 哨兵

AC代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 3e3 + 10;
int e[N], ne[N], h[N], idx, w[N], st[N], f[N][3];
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u)
{
    int sum = 0;
    f[u][2] = w[u];
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int v = e[i];
        dfs(v);
        f[u][0] += min(f[v][1], f[v][2]);
        f[u][2] += min(f[v][0], min(f[v][1], f[v][2]));
        sum += min(f[v][1], f[v][2]);
    }
    f[u][1] = 1e9;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        f[u][1] = min(f[u][1], sum - min(f[j][1], f[j][2]) + f[j][2]);
    }
}
int main()
{
    memset(h, -1, sizeof h);
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        int ver, t;
        cin >> ver >> w[ver] >> t;
        while (t--)
        {
            int x;
            cin >> x;
            add(ver, x);
            st[x] = true;
        }
    }
    int root = 1;
    while (st[root])
        root++;
    dfs(root);
    cout << min(f[root][1], f[root][2]);
}```

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53