LeetCode算法之拓扑排序

1 什么是拓扑排序

先看一个例子，大学排课（整理出先后依赖顺序），以计算机专业为例，如下表所示，想线上数据结构时候，必选先修C1和C2。如果课程比较少可以人肉排下，如果课程比较多，就需要借助相应工具或者算法来解决。

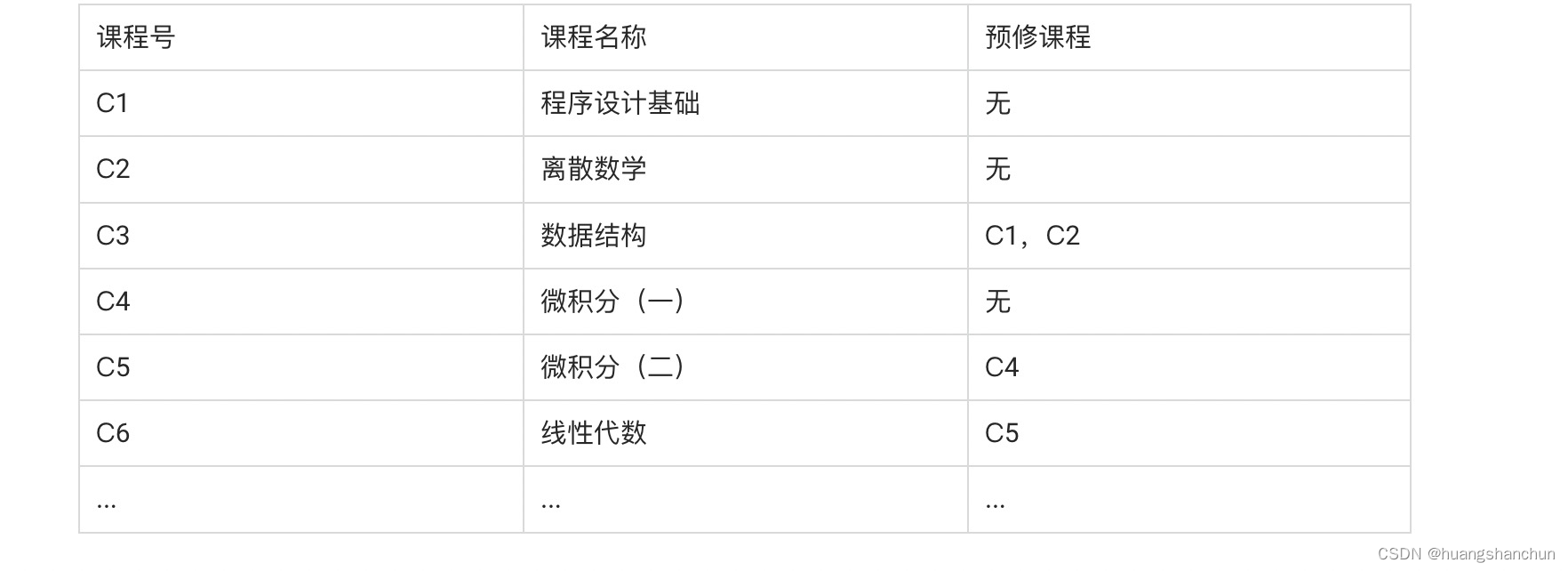
可以使用图来描述这个问题，每一门课为顶点，如果有预修课程，则该两个顶点有一条有向边（预修课程指向后续课程），如下图所示上面排课可以抽象描述为如下。这种图叫AOV网络（Activity on Vertex），活动是表现在顶点上的，顶点之间的有向边表示两个活动的先后顺序。

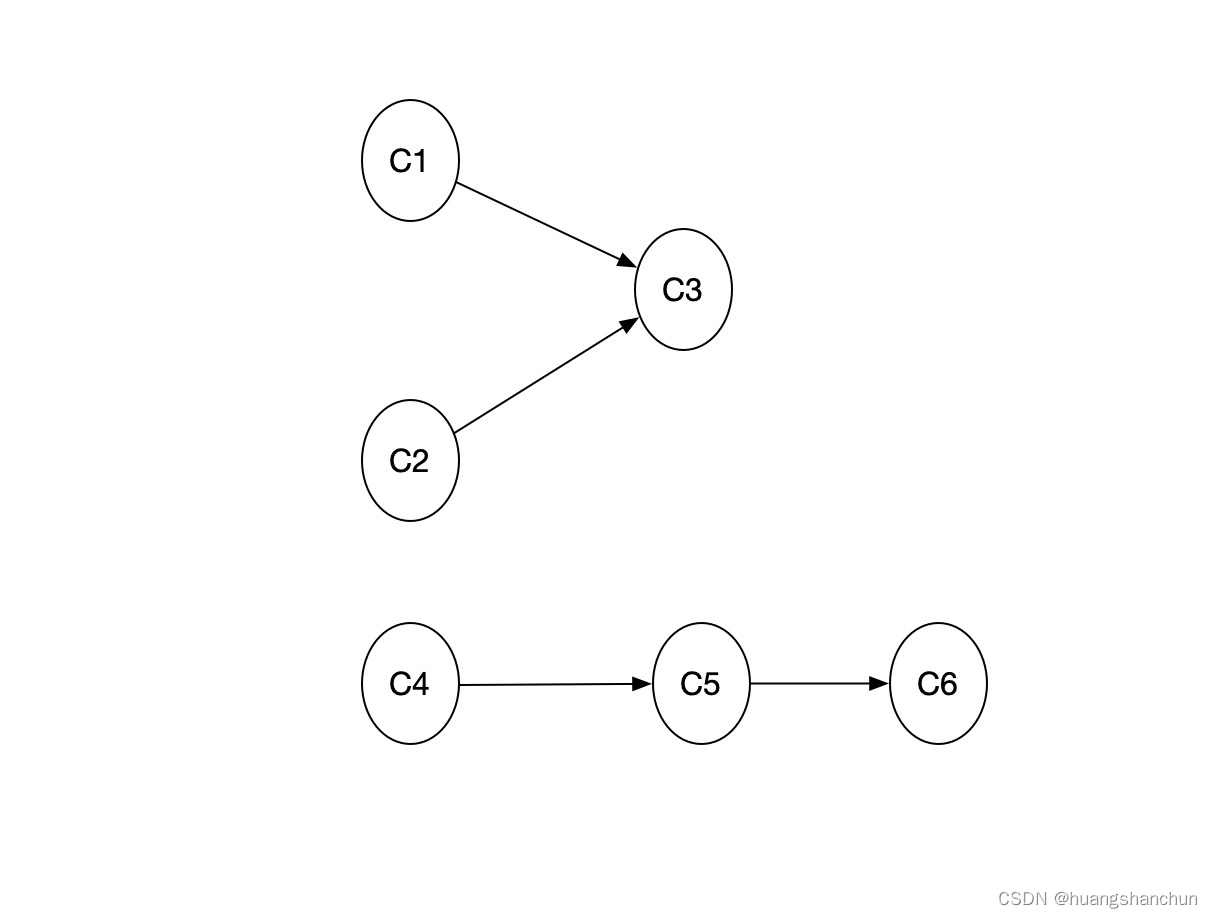
定义：拓扑序，如果AOV图中从V到W有一条有向路径，则V一定排序在W之前；满足此条的顶点序列称为一个拓扑序；获得一个拓扑序的过程就是拓扑排序；AOV如果是合理拓扑序，则必定是有向无环图。

2 拓扑排序算法描述

对AOV网络进行拓扑排序方法和步骤如下：
● 从AOV图中选择一个入度为0的顶点并且输出。
● 从图中删除该顶点，并且删除从该顶点出发的全部有向边（指向顶点入度减一）。
● 重复上述两步，直到剩余的顶点中不再存没有入度为0的顶点为止。最后如果最后还存在入度不为0的顶点，说明图中存在回路或者环。

void topSort(){
    //
    for(图中每个顶点V）{
        if(V顶点入度为0）
           Enqueue(V,Q);
      }
    
    while(!Q.isEmpty()) {
        V=Dequeue(Q);
        输出V，cnt++;
        for(V指向顶点 W）{
           W顶点入度减一;
           if(W顶点入度为0）
             Enqueue(W,Q);
        }
 
    }
    if(cnt!=顶点数量）
      ERROR(存在环)
                
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

3 实战案例

课程表：
https://leetcode.cn/problems/course-schedule/

class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        Node[] vetex = new Node[numCourses];
        for (int i = 0; i <= numCourses - 1; i++) {
            vetex[i] = new Node();
        }
        for (int[] arr : prerequisites) {
            vetex[arr[1]].edge.add(arr[0]);
            vetex[arr[0]].inDegree++;
        }
        Stack<Node> stack = new Stack();
        for (Node node : vetex) {
            if (node.inDegree == 0) {
                stack.add(node);
            }
        }
        int cnt = 0;
        while (!stack.isEmpty()) {
            cnt++;
            Node node = stack.pop();
            for (Integer edge : node.edge) {
                vetex[edge].inDegree--;
                if (vetex[edge].inDegree == 0) {
                    stack.add(vetex[edge]);
                }
            }
        }
        return cnt == numCourses;
    }

    public static class Node {
        //表示该顶点指向顶点边，记录的指向顶点数组下标
        public List<Integer> edge = new ArrayList();
        public int inDegree = 0;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

课程表顺序
https://leetcode.cn/problems/QA2IGt/

class Solution {
    public int[] findOrder(int numCourses, int[][] prerequisites) {
        int[] res=new int[numCourses];
        if(canFinish(numCourses,prerequisites,res)){
            return res;
        }
        return new int[0];
    }
    public boolean canFinish(int numCourses, int[][] prerequisites,int[] res) {
        Node[] vetex = new Node[numCourses];
        for (int i = 0; i <= numCourses - 1; i++) {
            vetex[i]=new Node(i);
        }
        for (int[] arr : prerequisites) {
            vetex[arr[1]].edge.add(arr[0]);
            vetex[arr[0]].inDegree++;
        }
        Stack<Node> stack = new Stack();
        for (Node node : vetex) {
            if (node.inDegree == 0) {
                stack.add(node);
            }
        }
        int cnt = 0;
        while (!stack.isEmpty()) {
            Node node = stack.pop();
            res[cnt++]=node.data;
            for (Integer edge : node.edge) {
                vetex[edge].inDegree--;
                if (vetex[edge].inDegree == 0) {
                    stack.add(vetex[edge]);
                }
            }
        }
        return cnt == numCourses;
    }

    public static class Node {
        //表示该顶点指向顶点边，记录的指向顶点数组下标
        public List<Integer> edge = new ArrayList();
        public int inDegree = 0;
        public int data;
        public Node(int data) {
            this.data=data;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47