-
About Estimation with Cross-Validation
Cross-validation is a statistical method used to estimate the skill of machine learning models.
It is commonly used in applied machine learning to compare and select a model for a given predictive modeling problem.because it is easy to understand, easy to implement, and results in skill estimates that generally have a lower bias than other methods.
- That k-fold cross-validation is a procedure used to estimate the skill of the model on new data.
- There are common tactics that you can use to select the value of k for your dataset.
- There are commonly used variations on cross-validation such as stratified and repeated that are available in scikit-learn.
1.1 Tutorial Overview
- k-Fold Cross-Validation
- Configuration of k
- Worked Example
- Cross-Validation in Python
- Variances on Cross-Validation
1.2 k-Fold Cross-Validation
Cross-validation is a resampling procedure used to evaluate machine learning models on a limited data sample.The procedure has a single parameter called k that refers to the number of groups that a given data sample is to be split into.the procedure is often called k-fold cross-validation. When a specific value for k is chosen, it may be used in place of k in the reference to the model, such as k=10 becoming 10-fold cross-validation.
Cross-validation is primarily used in applied machine learning to estimate the skill of a machine learning model on unseen data. That is, to use a limited sample in order to estimate how the model is expected to perform in general when used to make predictions on data not used during the training of the model. It is a popular method because it is simple to understand and because it generally results in a less biased or less optimistic estimate of the model skill than other methods, such as a simple train/test split.
1. Shuffle the dataset randomly.
2. Split the dataset into k groups
3. For each unique group:
3.1 Take the group as a hold out or test data set
3.2 Take the remaining groups as a training data set
3.3 Fit a model on the training set and evaluate it on the test set
3.4 Retain the evaluation score and discard the model
4. Summarize the skill of the model using the sample of model evaluation scores
The results of a k-fold cross-validation run are often summarized with the mean of the model skill scores. It is also good practice to include a measure of the variance of the skill scores, such as the standard deviation or standard error
1.3 Configuration of k
The k value must be chosen carefully for your data sample. A poorly chosen value for k may result in a mis-representative idea of the skill of the model, such as a score with a high variance (that may change a lot based on the data used to fit the model), or a high bias, (such as an overestimate of the skill of the model). Three common tactics for choosing a value for k are as follows:
- Representative: The value for k is chosen such that each train/test group of data samples is large enough to be statistically representative of the broader dataset.
- k=10: The value for k is fixed to 10, a value that has been found through experimentation to generally result in a model skill estimate with low bias a modest variance.
- k=n: The value for k is fixed to n, where n is the size of the dataset to give each test sample an opportunity to be used in the hold out dataset. This approach is called leave-one-out cross-validation.
The choice of k is usually 5 or 10, but there is no formal rule. As k gets larger, the difference in size between the training set and the resampling subsets gets smaller. As this difference decreases, the bias of the technique becomes smaller
If a value for k is chosen that does not evenly split the data sample, then one group will contain a remainder of the examples. It is preferable to split the data sample into k groups with the same number of samples, such that the sample of model skill scores are all equivalent.
1.4 Worked Example
To make the cross-validation procedure concrete, let’s look at a worked example. Imagine we have a data sample with 6 observations:
[0.1, 0.2, 0.3, 0.4, 0.5, 0.6]The first step is to pick a value for k in order to determine the number of folds used to split the data. Here, we will use a value of k = 3. That means we will shuffle the data and then split the data into 3 groups. Because we have 6 observations, each group will have an equal number of 2 observations.
- Fold1: [0.5, 0.2]
- Fold2: [0.1, 0.3]
- Fold3: [0.4, 0.6]
We can then make use of the sample, such as to evaluate the skill of a machine learning algorithm. Three models are trained and evaluated with each fold given a chance to be the held out test set. For example:
- Model1: Trained on Fold1 + Fold2, Tested on Fold3
- Model2: Trained on Fold2 + Fold3, Tested on Fold1
- Model3: Trained on Fold1 + Fold3, Tested on Fold2
1.5 Cross-Validation in Python
We do not have to implement k-fold cross-validation manually. The scikit-learn library provides an implementation that will split a given data sample up. The KFold() scikit-learn class can be used. It takes as arguments the number of splits, whether or not to shuffle the sample, and the seed for the pseudorandom number generator used prior to the shuffle. For example, we can create an instance that splits a dataset into 3 folds, shuffles prior to the split, and uses a value of 1 for the pseudorandom number generator.
- # define cross-validation folds
- kfold = KFold(3, True, 1)
The split() function can then be called on the class where the data sample is provided as an argument. Called repeatedly, the split will return each group of train and test sets. Specifically, arrays are returned containing the indexes into the original data sample of observations to use for train and test sets on each iteration. For example, we can enumerate the splits of the indices for a data sample using the created KFold instance as follows:
- # enumerate splits
- for train, test in kfold.split(data):
- print('train: %s, test: %s' % (train, test))
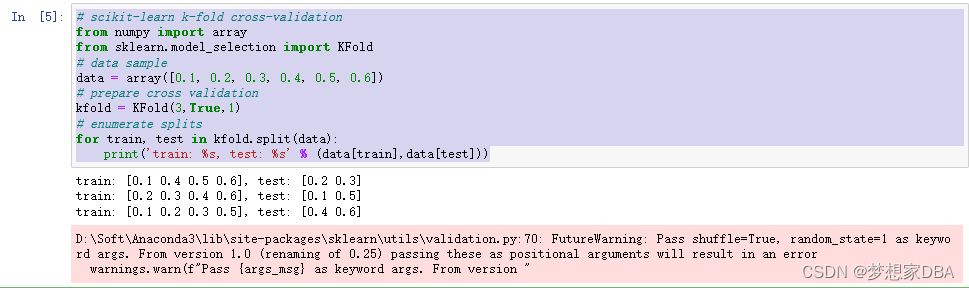
We can tie all of this together with our small dataset used in the worked example of the prior section.
- # scikit-learn k-fold cross-validation
- from numpy import array
- from sklearn.model_selection import KFold
- # data sample
- data = array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6])
- # prepare cross validation
- kfold = KFold(3,True,1)
- # enumerate splits
- for train, test in kfold.split(data):
- print('train: %s, test: %s' % (data[train],data[test]))
Running the example prints the specific observations chosen for each train and test set. The indices are used directly on the original data array to retrieve the observation values.
Usefully, the k-fold cross-validation implementation in scikit-learn is provided as a component operation within broader methods, such as grid-searching model hyperparameters and scoring a model on a dataset. Nevertheless, the KFold class can be used directly in order to split up a dataset prior to modeling such that all models will use the same data splits. This is especially helpful if you are working with very large data samples. The use of the same splits across algorithms can have benefits for statistical tests that you may wish to perform on the data later.
1.6 Variations on Cross-Validation
There are a number of variations on the k-fold cross-validation procedure. Three commonly used variations are as follows:
- Train/Test Split: Taken to one extreme, k may be set to 1 such that a single train/test split is created to evaluate the model.
- LOOCV: Taken to another extreme, k may be set to the total number of observations in the dataset such that each observation is given a chance to be the held out of the dataset. This is called leave-one-out cross-validation, or LOOCV for short.
- Stratified: The splitting of data into folds may be governed by criteria such as ensuring that each fold has the same proportion of observations with a given categorical value, such as the class outcome value. This is called stratified cross-validation.
- Repeated: This is where the k-fold cross-validation procedure is repeated n times, where importantly, the data sample is shuffled prior to each repetition, which results in a different split of the sample.
-
相关阅读:
BeanFactory和FactoryBean的区别
面试突击81:什么是跨域问题?如何解决?
制作本地Ceph镜像仓库(reposync下载、createrepo制作、httpd发布)
经典查找算法
MySQL入门:数据库是什么 | SQL是什么 | MySQL是什么
【附源码】计算机毕业设计JAVA大数据文章发布系统
【Java】接口
c语言编程 结构结合(union)
java 02- 标识符及数据类型
synchronized关键字在同步代码块中的应用(下)
- 原文地址:https://blog.csdn.net/u011868279/article/details/125623138