698. 划分为k个相等的子集 ●●

698. 划分为k个相等的子集 ●●

描述

给定一个整数数组 nums 和一个正整数 k，找出能否把这个数组分成 k 个非空子集，其总和都相等。

示例

输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明： 有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。

题解

参考链接

先对问题进行一层抽象：有 n 个球，k 个桶，如何分配球放入桶中使得每个桶中球的总和均为 target。如下图所示：

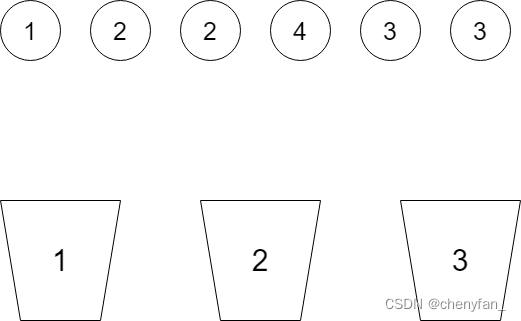
1. 回溯，球（数字）视角

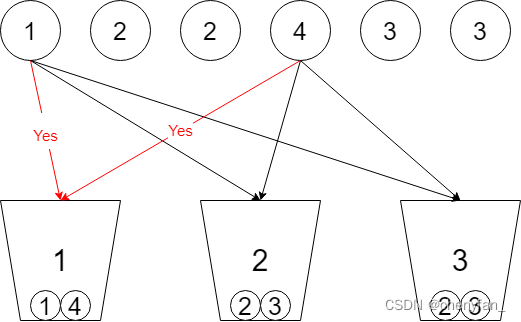
站在球的视角，每个球均需要做出三种选择，即：选择放入 1 号桶、2 号桶、3 号桶。所有球一共需要做 $k^n$ 次选择。

由于回溯就是一种暴力求解的思想，所以对于每个球的三种选择，只有执行了该选择才知道该选择是否为最优解。说白了就是依次执行这三种选择，如果递归到下面后发现该选择为非最优解，然后开始回溯，执行其他选择，直到把所有选择都遍历完。

剪枝操作至关重要。

class Solution {
public:
    bool backtrack(int idx, vector<int>& nums, vector<int>& buckets, int target, int k){
        if(idx == nums.size()) return true;                     // 结束条件：所有元素被分到了桶中，此时各集合和必定相等
        for(int i = 0; i < k; ++i){
            if (i > 0 && idx == 0) break ;                      // 第一个元素放到哪个桶都一样，所以回溯到第一个元素时则失败（剪枝）
            if(buckets[i] + nums[idx] > target) continue;       // 剪枝，集合和不能大于target
            if(i > 0 && buckets[i] == buckets[i-1]) continue;   // 剪枝，相同的集合和的选择可以看做是重复的情况
            buckets[i] += nums[idx];                            // 加入集合i
            if(backtrack(idx+1, nums, buckets, target, k)) return true; // 递归
            buckets[i] -= nums[idx];                            // 回溯
        }
        return false;                                           // k 个桶都不满足要求
    }   

    bool canPartitionKSubsets(vector<int>& nums, int k) {
        int sum = 0, maxNum = 0;
        for(int num : nums){
            sum += num;
            if(maxNum < num) maxNum = num;
        }
        if(maxNum*k > sum || sum % k != 0) return false;    // 剪枝
        int target = sum / k;                               // 目标集合和
        vector<int> buckets(k, 0);                          // 桶集合
        sort(nums.begin(), nums.end(), greater<int>());     // 降序，由大往小填，降低回溯的消耗
        return backtrack(0, nums, buckets, target, k);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

2. 回溯，桶（集合）视角

站在桶的视角，每个桶均需要做出六次选择，即：是否选择 1 号球放入、是否选择 2 号球放入、…、是否选择 6 号球放入。所有的桶一共需要做 $k{2}^n$ 次选择。

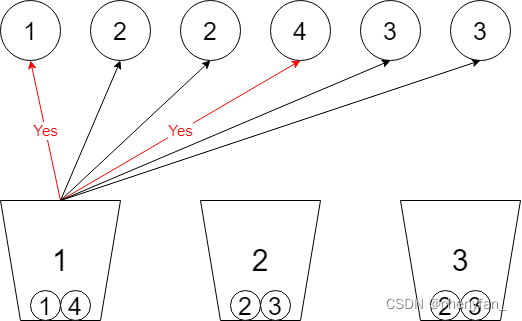
下面为「桶视角」下的决策树

首先解释一下这棵决策树，第 i 层为 j 号桶做出第 x 次选择，可做的选择：是否选择 1 ～ 6 号球，直到 k 个桶均装满后结束；

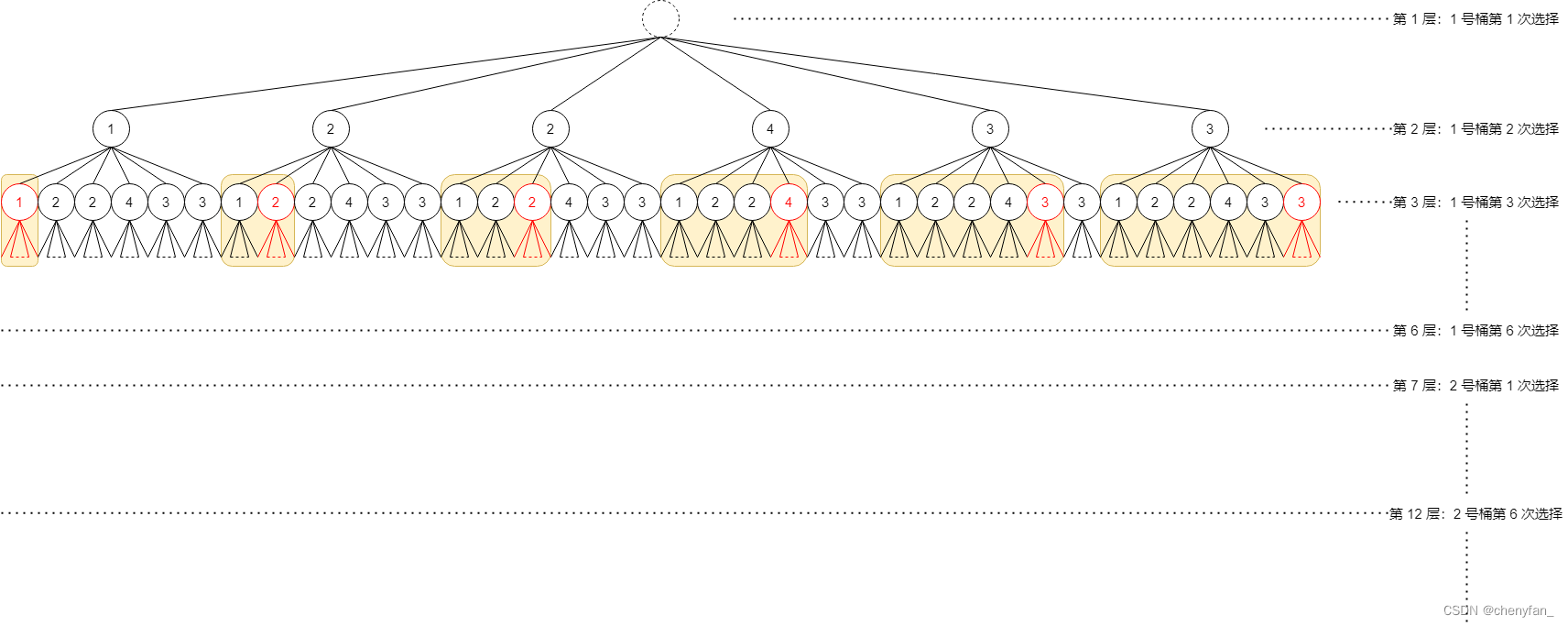
由于，每个球只能被一个桶选择，所以当某一个球被某一个桶选择后，另一个桶就不能选择该球，如下图红色标注出的分支；

判断是否可以选择某个球的条件为：(1) 该球是否已经被选择？ (2) 放入该球后，桶是否溢出？

数组有序情况下，排除下一个和当前的数值相同的情况的选择对于减小时间复杂度至关重要。

class Solution {
public:
    unordered_set<vector<bool>> hash;
    bool backtrack(int start, vector<int>& nums, vector<bool>& used, vector<int>& buckets, int target, int k){
        if(k == 0) return true;                                 // 结束条件：所有桶都装满了元素
        if(buckets[k-1] == target) return backtrack(0, nums, used, buckets, target, k-1);   // 当前桶装满了，开始装下一个桶
        for(int i = start; i < nums.size(); ++i){               // 遍历每个球，选择是否装入
            if(used[i] == true) continue;                       // 该球已被使用
            if(buckets[k-1] + nums[i] > target) continue;       // 剪枝，集合和不能大于target
            used[i] = true;                                     // 选择该球加入桶
            buckets[k-1] += nums[i];                            
            if(backtrack(i+1, nums, used, buckets, target, k)) return true; // 递归，从下一个球开始
            buckets[k-1] -= nums[i];                            // 回溯
            used[i] = false;        
            while (i + 1 < nums.size() && nums[i + 1] == nums[i]) ++i;      // 剪枝，有序情况下，下一个如果和当前的相同肯定也不行
        }
        return false;                                           // 所有球都无法满足条件
    }   

    bool canPartitionKSubsets(vector<int>& nums, int k) {
        int sum = 0, maxNum = 0;
        for(int num : nums){
            sum += num;
            if(maxNum < num) maxNum = num;
        }
        if(maxNum*k > sum || sum % k != 0) return false;    // 剪枝
        int target = sum / k;                               // 目标集合和
        vector<int> buckets(k, 0);                          // 桶集合
        vector<bool> used(nums.size(), false);              // 使用标记
        sort(nums.begin(), nums.end());                     // 排序
        return backtrack(0, nums, used, buckets, target, k);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

• 数组大小最大为16个，因此 bool 数组标记的形式可以利用位操作标记来进行优化

int used = 0; 初始化
(used >> i) & 1 == 1 判断第 i 个数是否已使用
used |= 1 << i; 标记第 i 个数
used ^= 1 << i;第 i 个数取消标记