• 【手撕STL】AVL树

    AVL树

    AVL树的概念

    二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此，找到了解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

    AVL树的性质：

    • 它的左右子树都是AVL树
    • 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
    • 如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在 O(logN)，搜索时间复杂度O(logN)。

    注：平衡因子=右子树的高度-左子树的高度

    平衡因子更新规则：

    • 插入更新的节点在父亲的左边，父亲平衡因子–；插入更新的节点在父亲的右边，父亲平衡因子++
    • 父亲的平衡因子更新以后是-1或者1，说明父亲所在子树的高度变了，需要继续往上更新
    • 父亲的平衡因子更新以后是0，说明父亲所在子树的高度没变，不需要继续往上更新
    • 父亲的平衡因子更新以后是-2或者2，说明父亲所在子树已经不平衡了，需要旋转处理使它平衡
    • 更新以后，更新到了根节点就不需要在更新了

    AVL树的旋转

    如果在一棵原本是平衡的AVL树中插入一个新节点，可能造成不平衡，此时必须调整树的结构，使之平衡化。根据节点插入位置的不同，AVL树的旋转分为四种：

    新节点插入较高左子树的左侧—左左：右单旋

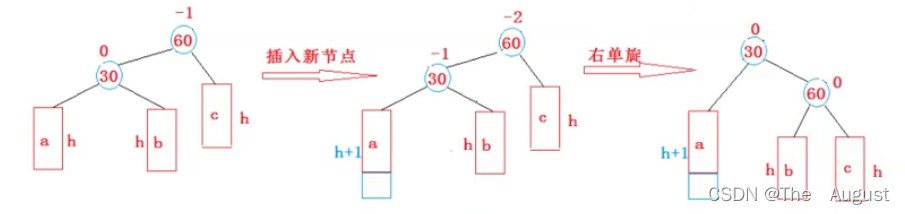
    在这里插入图片描述

    a，b，c是高度为h的AVL子树，他们有无数种情况，只要在a中插入节点，a的高度变为h+1，就会引发右单旋（h>=0）

    右单旋操作：

    1. b子树变成60的左子树
    2. 60成为30的右子树，30成为这棵树的根
    3. 30和60的平衡因子变为0

    新节点插入较高右子树的右侧—右右：左单旋
    在这里插入图片描述
    a，b，c是高度为h的AVL子树，只要c这棵子树的高度变为h+1，就会引发左单旋

    左单旋操作：

    1. b子树变成30的右子树
    2. 30成为60的左子树，60成为这棵树的根
    3. 30和60的平衡因子变为0

    新节点插入较高左子树的右侧—左右：先左单旋再右单旋
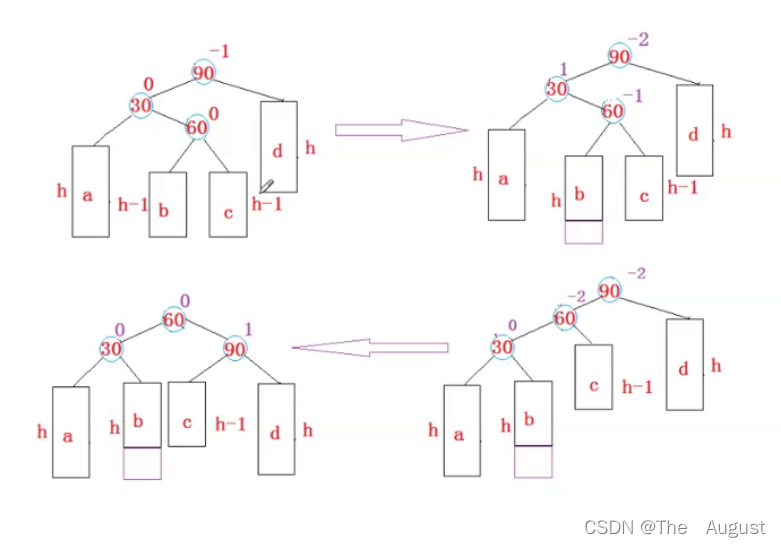
    在这里插入图片描述
    操作：

    • 先以30为旋转点，进行左单旋
    • 以90作为旋转点进行右单旋

    新节点插入较高右子树的左侧—右左：先右单旋再左单旋
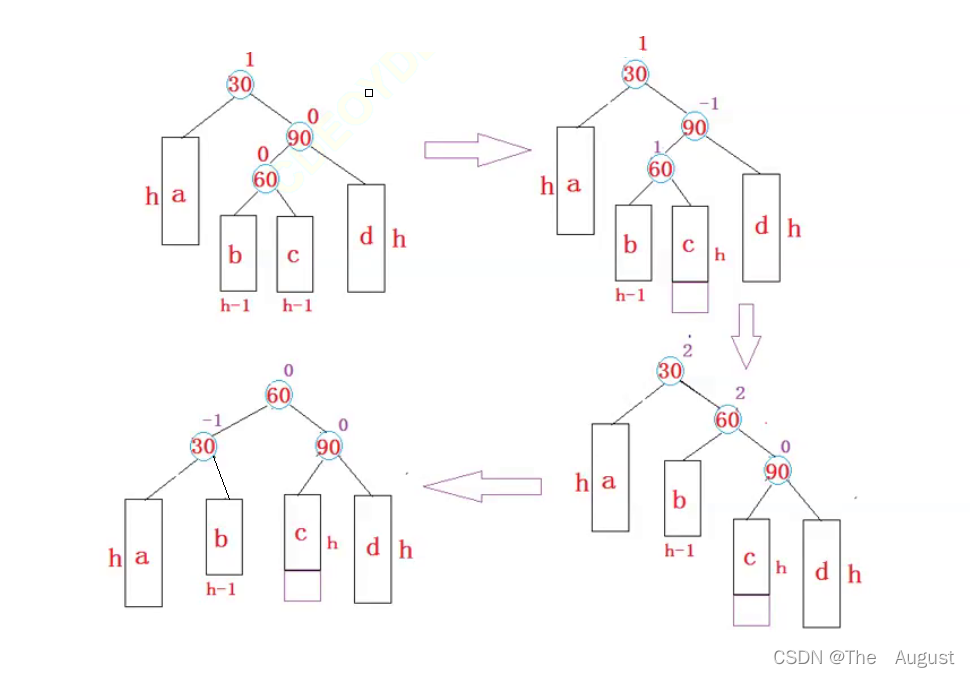
    在这里插入图片描述

    操作：

    • 先以90为旋转点，进行右单旋
    • 以30作为旋转点进行左单旋

    双旋平衡因子更新问题：
    在这里插入图片描述
    双旋以后的结果：

    • b变成30的右边
    • c变成60的左边
    • 30和90分别变成60的左边和右边，60成为新的根

    总结：

    • 旋转的本质：在遵循搜索树的规则情况，让左右均衡，并且降低整棵树的高度
    • 更新平衡因子的过程中，引发旋转的路径是直线就是单旋，如果是折线就是双旋

    总结：
    假如以pParent为根的子树不平衡，即pParent的平衡因子为2或者-2，分以下情况考虑

    1. pParent的平衡因子为2，说明pParent的右子树高，设pParent的右子树的根为pSubR
    • 当pSubR的平衡因子为1时，执行左单旋
    • 当pSubR的平衡因子为-1时，执行右左双旋
    1. pParent的平衡因子为-2，说明pParent的左子树高，设pParent的左子树的根为pSubL
    • 当pSubL的平衡因子为-1是，执行右单旋
    • 当pSubL的平衡因子为1时，执行左右双旋

    旋转完成后，原pParent为根的子树个高度降低，已经平衡，不需要再向上更新。

    AVL树的实现

    #pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<assert.h>
#include<iostream>
using namespace std;

template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _bf(0)
	{}

	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	int _bf;   //balance factor= 右树的高度-左树的高度
};



template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	AVLTree()
		:_root(nullptr)
	{}
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first > kv.first)
		{
			parent->_left = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		//控制树的平衡
		
		while (parent)
		{
			//更新平衡因子
			if (parent->_left == cur)
				parent->_bf--;
			else
				parent->_bf++;
			//检查父亲的平衡因子
			//父亲所在子树的高度不变，不影响祖先，跟新结束

			if (parent->_bf == 0)
				break;
			//父亲所在子树高度变了，继续往上更新
			else if (parent->_bf == -1 || parent->_bf == 1)
			{
				cur = parent;
				parent = cur->_parent;
			}
			//父亲所在子树的出现了不平衡，需要旋转处理
			else if (parent->_bf == -2 || parent->_bf == 2)
			{
				if (parent->_bf == -2 && cur->_bf == -1)
				{
					RotateR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					RotateLR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					RotateRL(parent);
				}
				else
				{
					assert(false);
				}
				break;


			}
			
			else
			{
				assert(false);
			}
		}
		return true;
	}


	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		
		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}
		Node* ppNode = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;
		if (parent == _root)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (ppNode->_left == parent)
				ppNode->_left = subL;
			else
				ppNode->_right = subL;

			subL->_parent = ppNode;
		}
		subL->_bf = parent->_bf = 0;
	}
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
		{
			subRL->_parent = parent;
		}
		Node* ppNode = parent->_parent;

		subR->_left = parent;
		parent->_parent = subR;
		if (parent == _root)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (ppNode->_left == parent)
				ppNode->_left = subR;
			else
				ppNode->_right = subR;

			subR->_parent = ppNode;
		}
		subR->_bf = parent->_bf = 0;
	}

	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		if (bf == 1)
		{
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}
	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		if (bf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subR->_bf = 1;
			subRL->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}
	int Height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int leftHeight = Height(root->_left);
		int rightHeight = Height(root->_right);
		return leftHeight > rightHeight ? ++leftHeight : ++rightHeight;
	}
	bool IsBalance()
	{
		return _IsBalance(_root);
	}
private:

	bool _IsBalance(Node* root)
	{
		if (root == nullptr)
			return true;
		int leftHeight = Height(root->_left);
		int rightHeight = Height(root->_right);

		if (rightHeight - leftHeight != root->_bf)
			cout << "平衡因子异常:" << root->_kv.first << endl;
		return abs(rightHeight - leftHeight) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);
	}

	Node* _root;

};


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119
    • 120
    • 121
    • 122
    • 123
    • 124
    • 125
    • 126
    • 127
    • 128
    • 129
    • 130
    • 131
    • 132
    • 133
    • 134
    • 135
    • 136
    • 137
    • 138
    • 139
    • 140
    • 141
    • 142
    • 143
    • 144
    • 145
    • 146
    • 147
    • 148
    • 149
    • 150
    • 151
    • 152
    • 153
    • 154
    • 155
    • 156
    • 157
    • 158
    • 159
    • 160
    • 161
    • 162
    • 163
    • 164
    • 165
    • 166
    • 167
    • 168
    • 169
    • 170
    • 171
    • 172
    • 173
    • 174
    • 175
    • 176
    • 177
    • 178
    • 179
    • 180
    • 181
    • 182
    • 183
    • 184
    • 185
    • 186
    • 187
    • 188
    • 189
    • 190
    • 191
    • 192
    • 193
    • 194
    • 195
    • 196
    • 197
    • 198
    • 199
    • 200
    • 201
    • 202
    • 203
    • 204
    • 205
    • 206
    • 207
    • 208
    • 209
    • 210
    • 211
    • 212
    • 213
    • 214
    • 215
    • 216
    • 217
    • 218
    • 219
    • 220
    • 221
    • 222
    • 223
    • 224
    • 225
    • 226
    • 227
    • 228
    • 229
    • 230
    • 231
    • 232
    • 233
    • 234
    • 235
    • 236
    • 237
    • 238
    • 239
    • 240
    • 241
    • 242
    • 243
    • 244
    • 245
    • 246
    • 247
    • 248
    • 249
    • 250
    • 251
    • 252
    • 253
    • 254
    • 255
    • 256
    • 257
    • 258
    • 259
    • 260
    • 261
    • 262
    • 263
    • 264
    • 265
    • 266
    • 267
    • 268
    • 269
    • 270
    • 271
    • 272
    • 273
    • 274
    • 275
    • 276
    • 277
    • 278
    • 279
    • 280
    • 281
    • 282
    • 283

    AVL树的验证

    AVL树是在二叉搜索树的基础上加入了平衡性的限制，因此要验证AVL树，可以分两步：

    1. 验证其为二叉搜索树
    • 如果中序遍历可得到一个有序的序列，就说明为二叉搜索树
    1. 验证其为平衡树
    • 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
    • 节点的平衡因子是否计算正确
    1. 验证用例
    • 常规场景:{16, 3, 7, 11, 9, 26, 18, 14, 15}
    • 特殊场景:{4, 2, 6, 1, 3, 5, 15, 7, 16, 14}

    AVL树的删除:

    • 按二叉搜索树的思路进行删除
    • 更新平衡因子（删除左节点，该父亲节点++；删除右节点，该父亲节点–）
    • 当父亲节点平衡因子为1或者-1时，不需要往上更新；当父亲节点平衡因子为0时，需要往上更新
    • 如果出现不平衡，进行旋转（注意父节点的平衡因子（高度变了））

    AVL树的性能

    AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即logN 。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。

  • 相关阅读:
    Android笔试面试题AI答之Kotlin（3）
    IPSec 基础介绍
    CentOS Install Passenger for ROR
    STM32 定时器定时中断
    Java实战项目-基于SpringBoot的新能源汽车个性化推荐系统
    《Linux驱动：s3c2410/s3c2440 ts驱动分析 之二》
    javaweb电脑销售管理系统的设计
    群晖linux ——设置短密码、免密码登录、多个群晖免密登录
    性能测试-基础篇
    2022VLMo: Unified Vision-Language Pre-Training with Mixture-of-Modality-Experts
  • 原文地址：https://blog.csdn.net/AI_ELF/article/details/123042060