-
DFS和BFS概念及实践
DFS (深搜), 也有说就是递归的
执着: 一直搜到底,然后回溯下一个节点
数据结构 : stack, 空间:O(h) h: 是高度
不具有最短路性质(思路比较奇怪的,对空间要求比较高的)
重要概念: 回溯,剪枝BFS (宽搜)
稳重:一层一层搜索
数据结构 : queue, 空间:O(2h) h: 是高度
具有最短路性质(当每条路权重是1)
DFS 例题讲解:可以用来理解递归的思想
给定一个整数 n,将数字 1∼n 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。输入格式
共一行,包含一个整数 n。
输出格式
按字典序输出所有排列方案,每个方案占一行。数据范围
1≤n≤7
输入样例:
3
输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1思想:
对于全排列问题,可以画出下面的搜索树
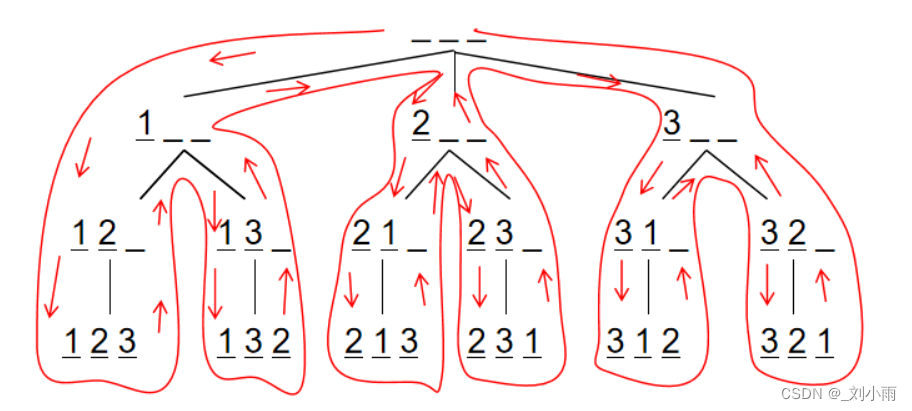
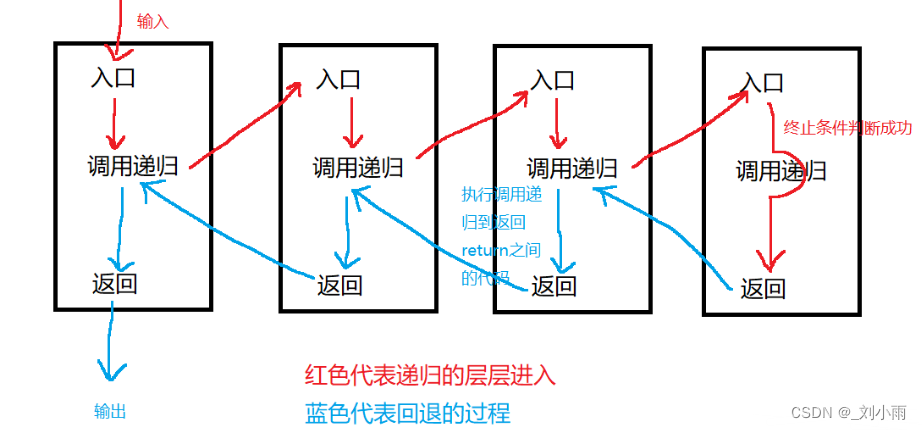
递归函数调用全过程
code:// 回溯的时候是系统中自动分配的栈回调。 #include <iostream> using namespace std; const int N = 10; int n; int path[N]; bool st[N]; // 保存之前的点是否遍历 == true 表示已经过了 void dfs(int u) { if(u == n) { // 说明所有的位置填满, 这里从0开始,在main函数中,对应的从0开始 for(int i=0; i<n; i++) cout << path[i] << ' '; cout << endl; return; } // 这里是确定哪几个点可以被选择 for(int i=1; i<=n; i++) // 这里需要找哪些点没有被枚举 { if(!st[i]) { path[u] = i; st[i] = true; dfs(u+ 1); // 恢复现场 st[i] = false; //path[u] = 0; // 可以删掉, 因为这里的值被覆盖掉 } } } int main() { cin >> n; dfs(0); // 从第0个位置开始看 return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
讲解上述代码流程:
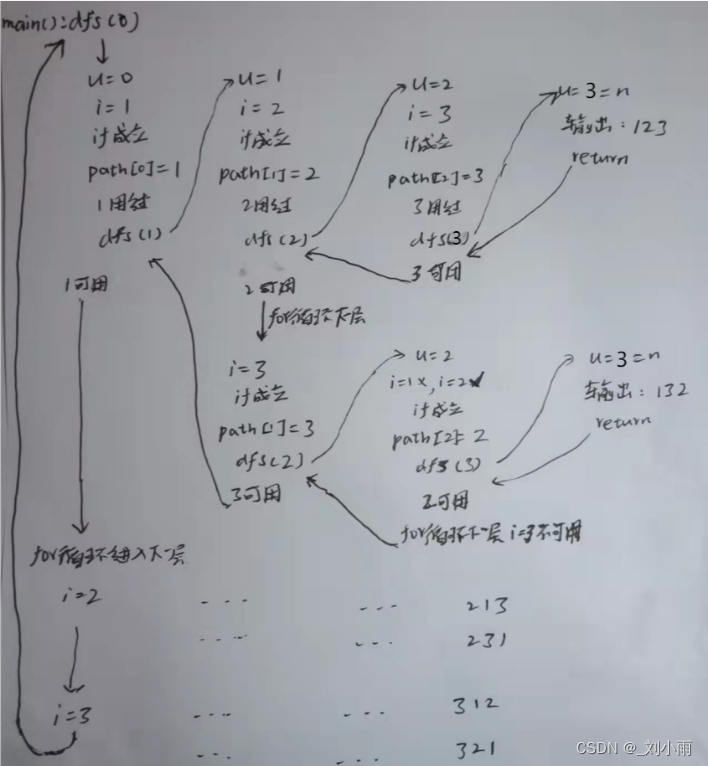
-
相关阅读:
javaEE7
Git 详细安装教程(详解 Git 安装过程的每一个步骤)
nginx(三十七)在线预览pdf文件
Flink的检查点和保存点
基于鹈鹕算法优化概率神经网络PNN的分类预测 - 附代码
支付、结算、对账流程
设备安装CoreELEC系统,并配置遥控
数字孪生与智慧城市:重塑未来城市生活的奇迹
471-82(647、5、92、143、148、19)
Python数学计算工具4、Python求最大公约数
- 原文地址:https://blog.csdn.net/qq_39486027/article/details/125616160