1. 树与树算法

1.1 树的概念

树(英语: tree)是一种抽象数据类型（ADT）或是实作这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由 $n(n>=1)$ 个有限节点组成一个具有层次关系的集合。把它叫做“树""是因为看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点:

• 每个节点有零个或多个子节点;
• 没有父节点的节点称为根节点;
• 每一个非根节点有且只有一个父节点;
• 除了根节点外，每个子节点可以分为多个不相交的子树;

比如说：

---

---

---

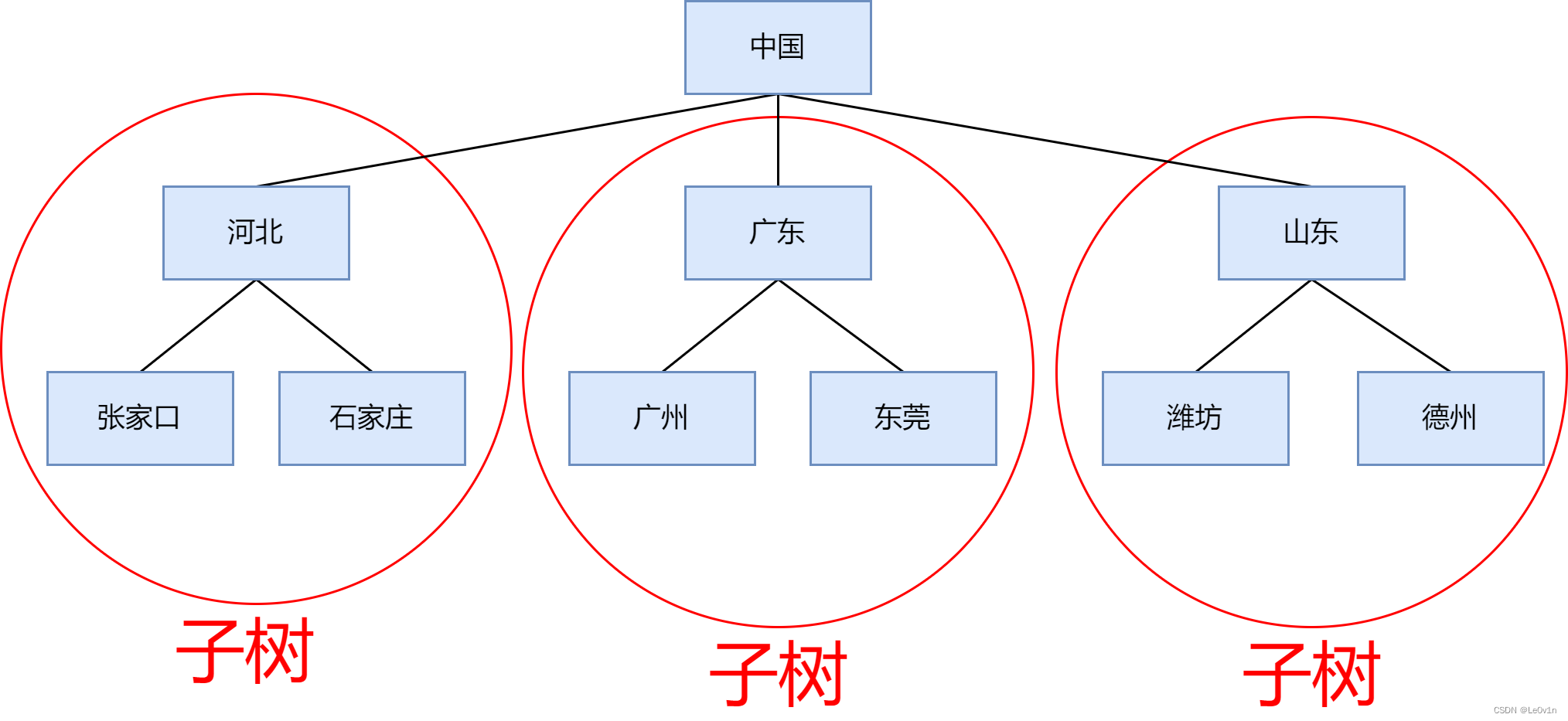
1.2 树的术语

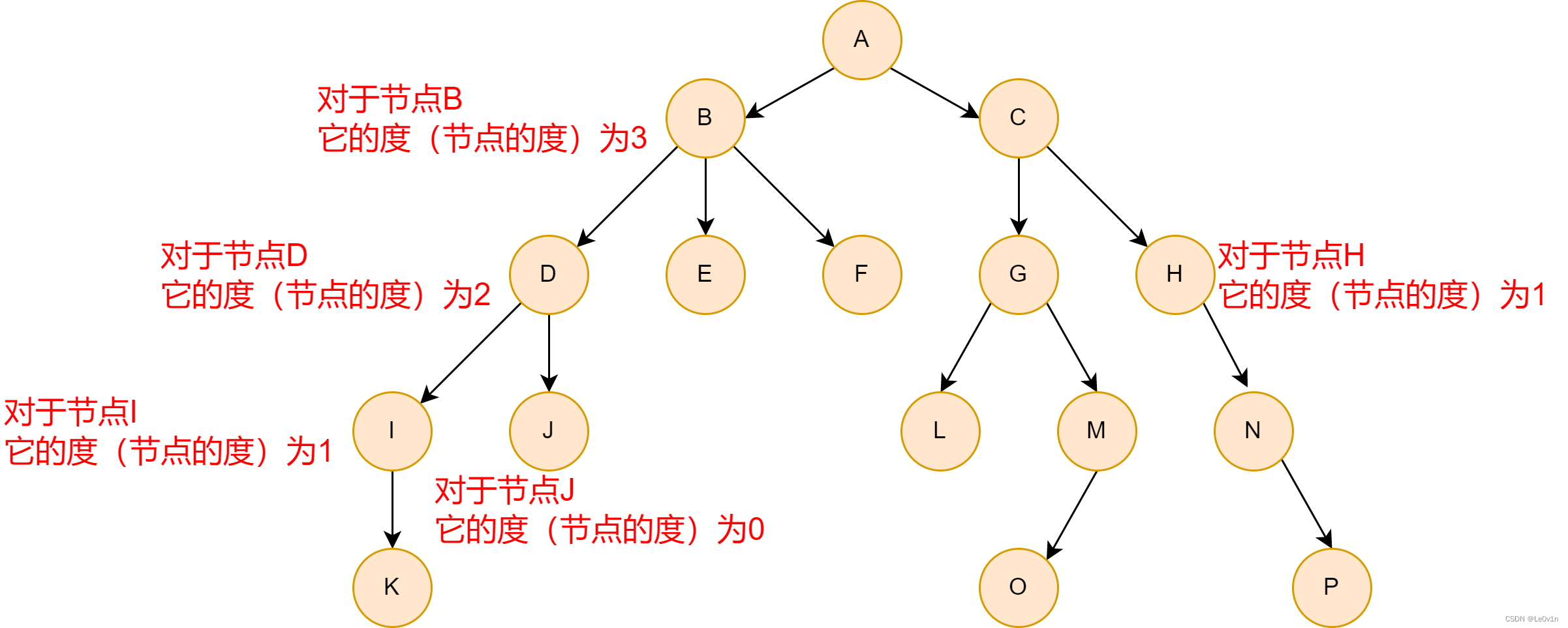
• 节点的度: 一个节点含有的子树的个数称为该节点的度;
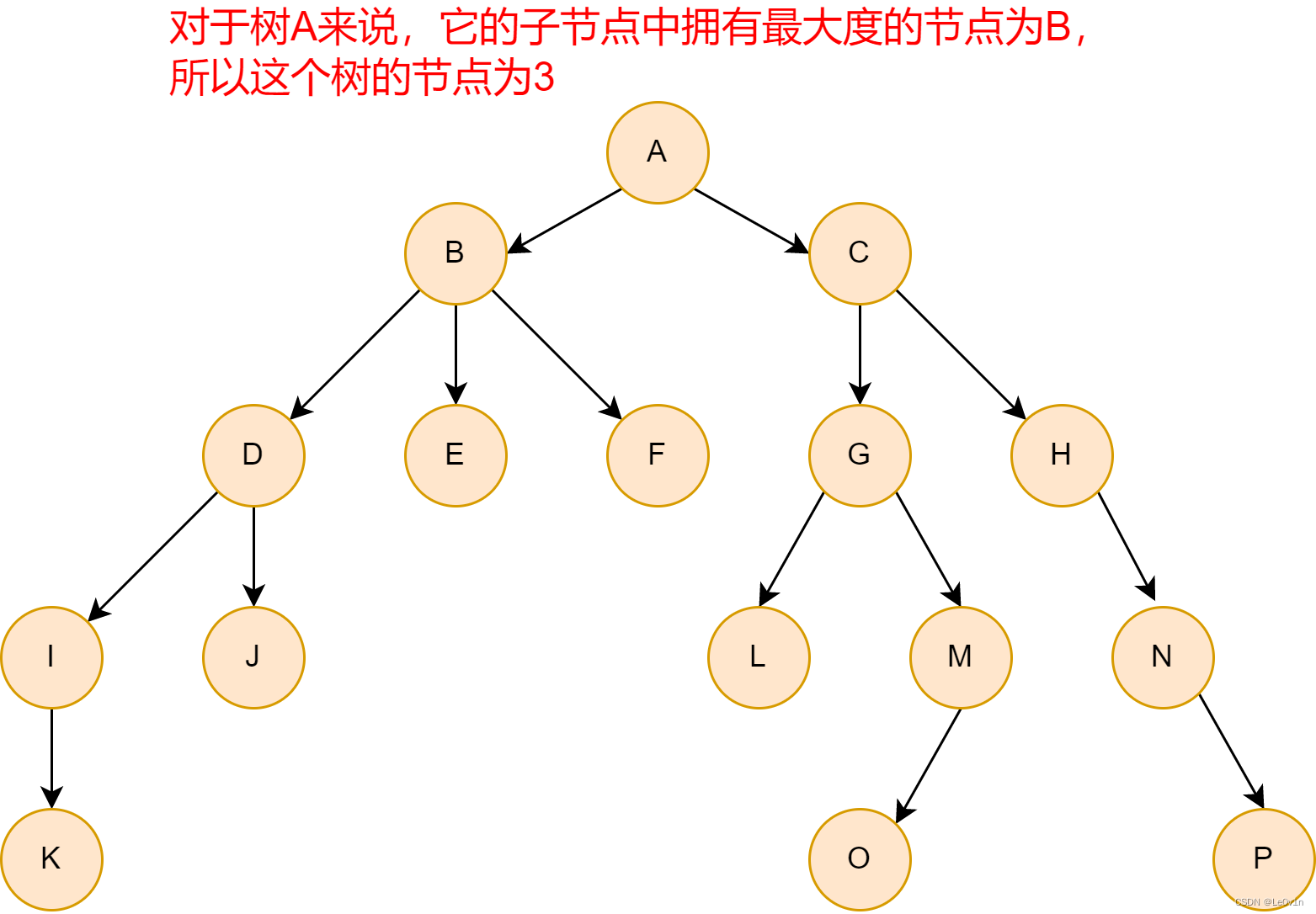
• 树的度: 一棵树中，最大的节点的度称为树的度;
• 叶节点或终端节点: 度为零的节点;
• 父亲节点或父节点: 若一个节点含有子节点，则这个节点称为其子节点的父节点;
• 孩子节点或子节点: 一个节点含有的子树的根节点称为该节点的子节点;
• 兄弟节点: 具有相同父节点的节点互称为兄弟节点;
• 节点的层次: 从根开始定义起，根为第1层，根的子节点为第2层，以此类推;
• 树的高度或深度: 树中节点的最大层次;
• 堂兄弟节点: 父节点在同一层的节点互为堂兄弟;
• 节点的祖先: 从根到该节点所经分支上的所有节点;
• 子孙: 以某节点为根的子树中任一节点都称为该节点的子孙；
• 森林: 由 $m(m\le 0)$棵互不相交的树的集合成为森林（这里即便是一棵树，也可以称为森林）。

1.2.1 节点的度

1.2.2 树的度

1.2.3 叶子节点或终端节点

1.2.4 父亲节点或父节点

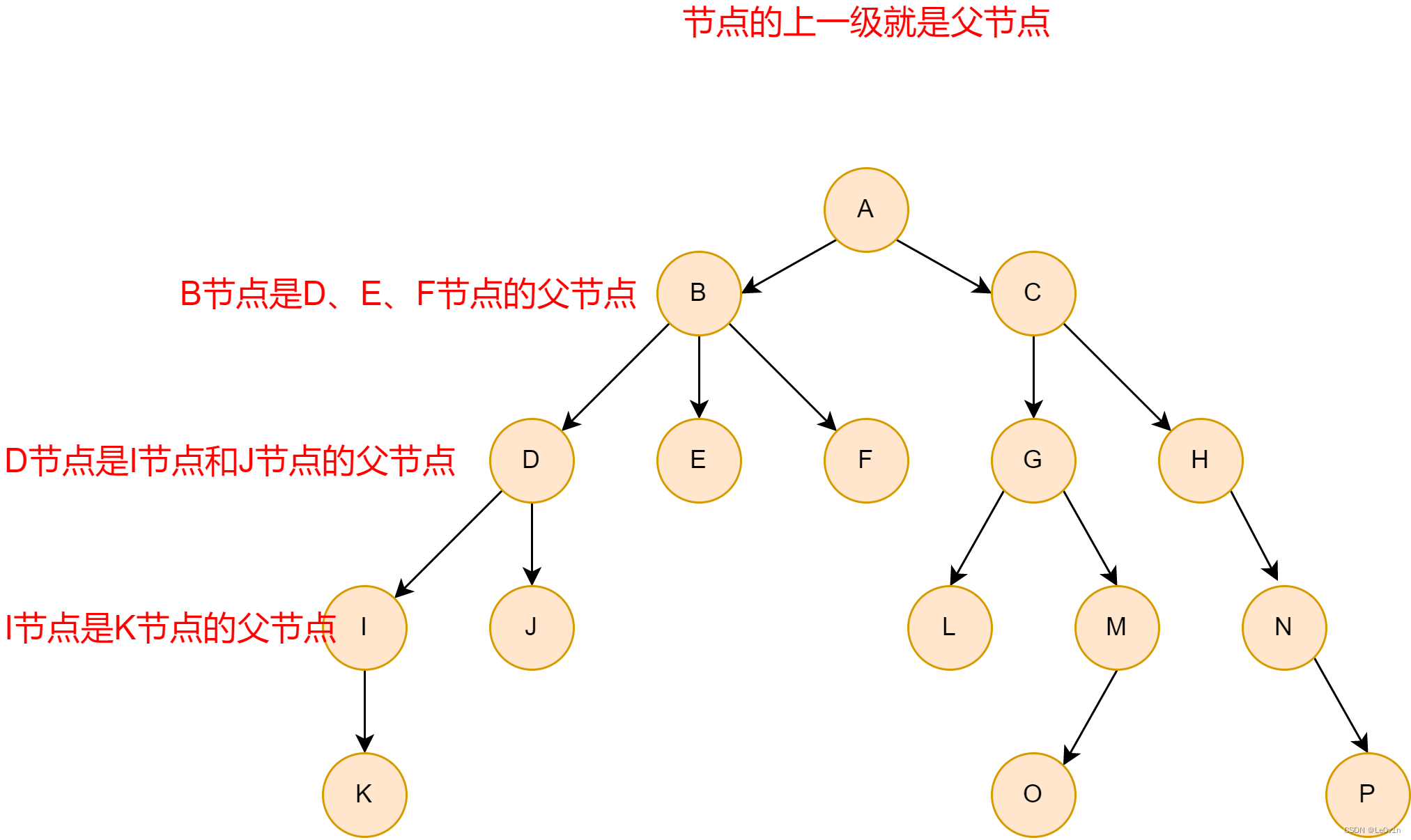
1.2.5 孩子节点或子节点

和父节点是反着来着，就不画图了。

1.2.6 兄弟节点

1.2.7 节点的层次

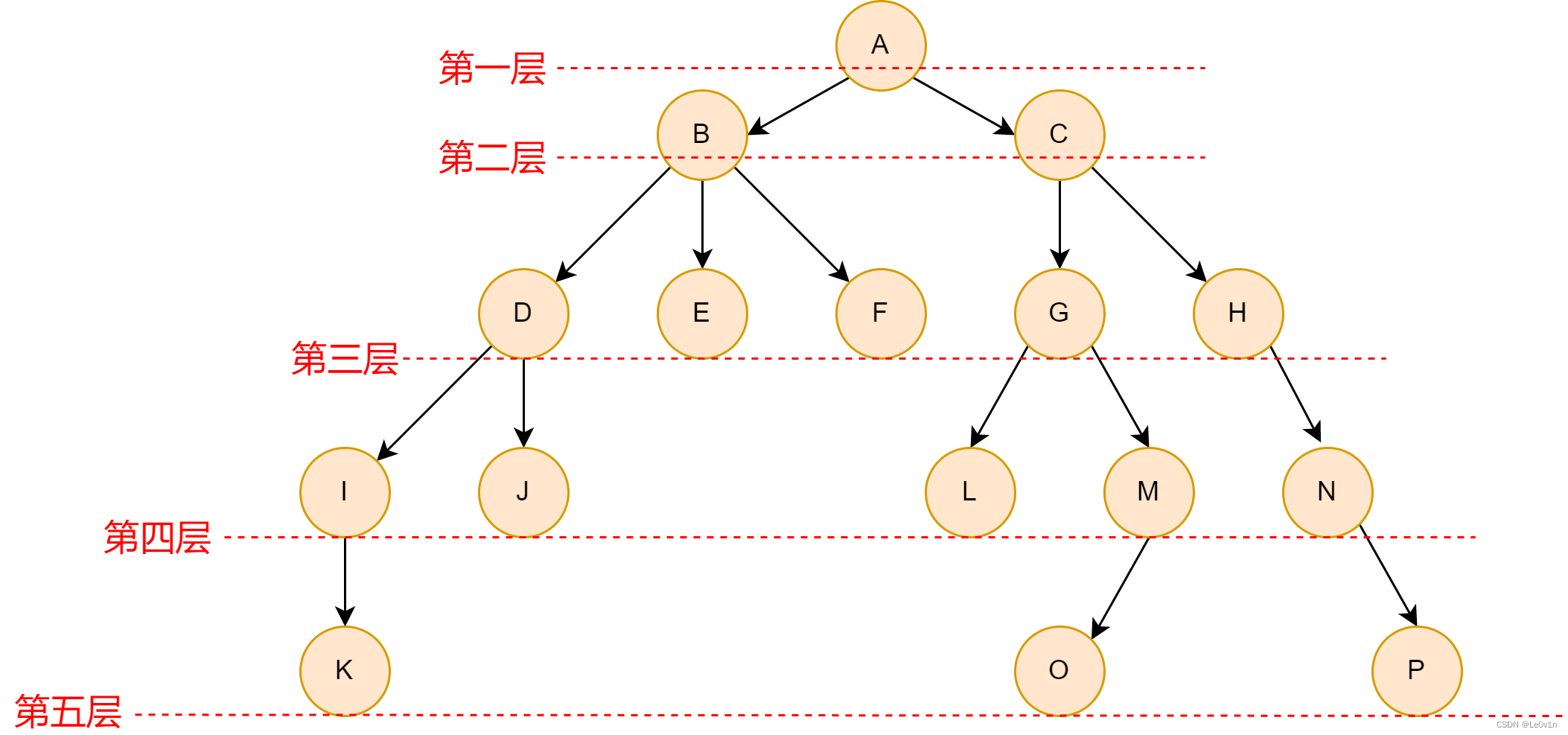
1.2.8 节点的层次树的高度或深度

就是最大的节点层次（根节点是第一层）。

1.2.9 堂兄弟节点

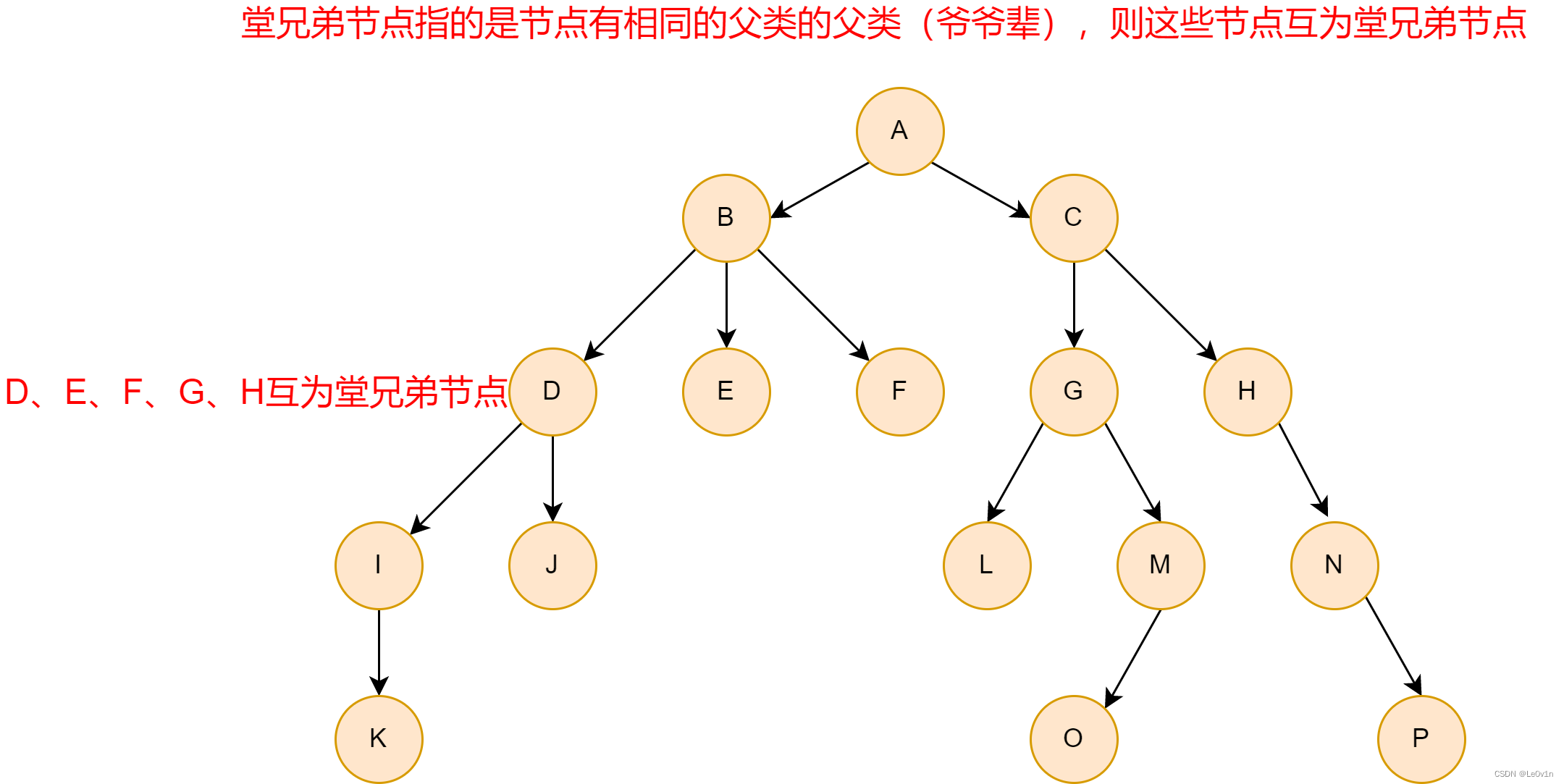
1.2.10 节点的祖先

1.2.11 子孙

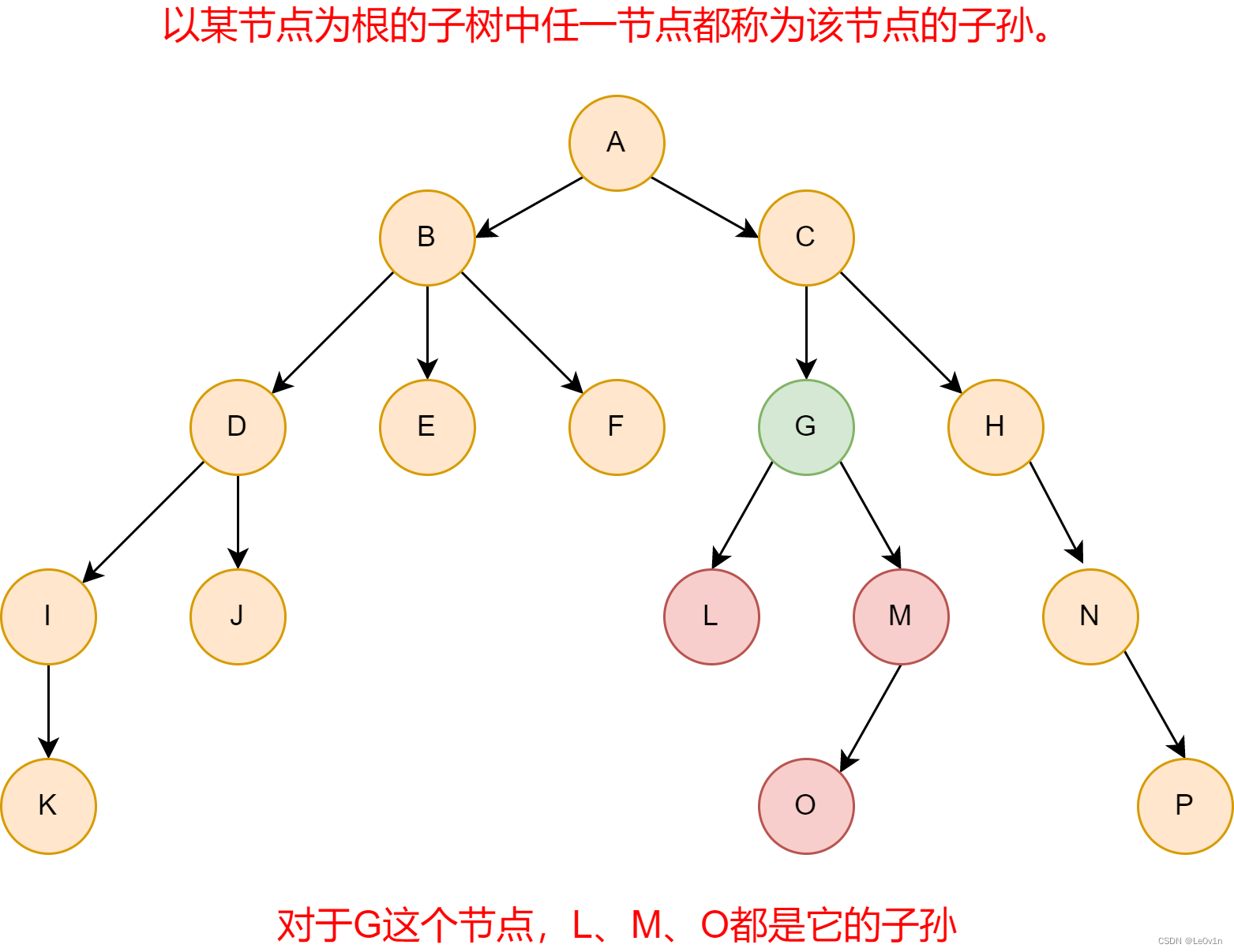
1.2.12 森林

1.3 树的种类

• 无序树:树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树 -> 对于这样的无序树，本身并没有什么研究价值;
• 有序树:树中任意节点的子节点之间有顺序关系，这种树称为有序树 -> 有序树的顺序结构是有某种关系的，有很大的研究价值;
  • 二叉树:每个节点最多含有两个子树的树称为二叉树;
    • 完全二叉树:对于一颗二叉树，假设其深度为 $d(d>1)$。除了第 $d$ 层外，其它各层的节点数目均已达最大值，且第 $d$ 层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树。
      其中满二叉树的定义是所有叶节点都在最底层的完全二叉树;
    • 平衡二叉树(AVL树)︰当且仅当任何节点的两棵子树的高度差不大于1的二叉树;
    • 排序二叉树(二叉查找树（英语:Binary Search Tree)，也称二叉搜索树、有序二叉树)
  • 霍夫曼树（用于信息编码)∶带权路径最短的二叉树称为哈夫曼树或最优二叉树;
  • B树:一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多余两个子树。

2. 树的存储与表示

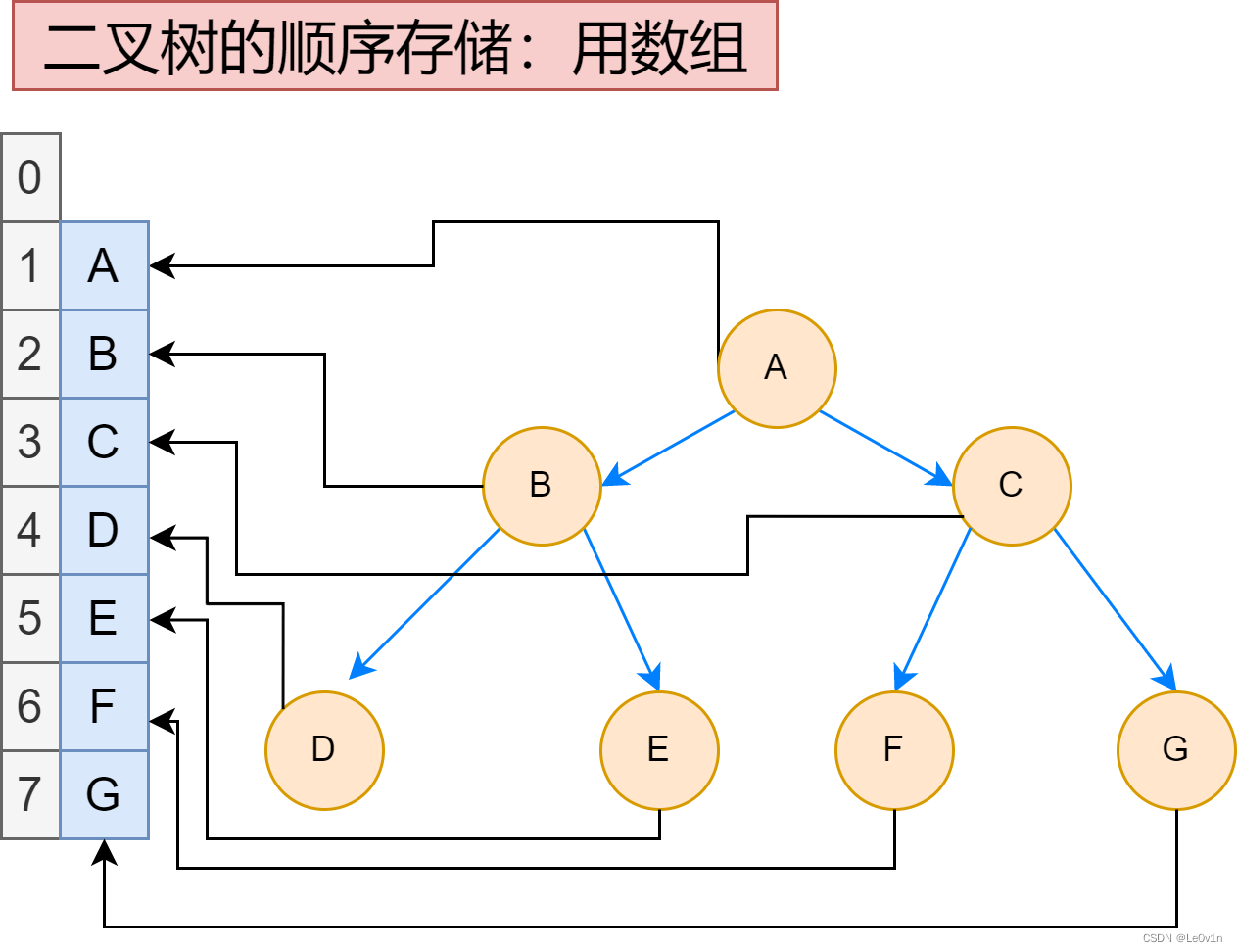
2.1 顺序存储

将数据结构存储在固定的数组中，然在遍历速度上有一定的优势，但因所占空间比较大，是非主流二叉树。二叉树通常以链式存储。

2.2 链式存储

树长成什么样子，我们就在构造的时候将其构造为什么样子。

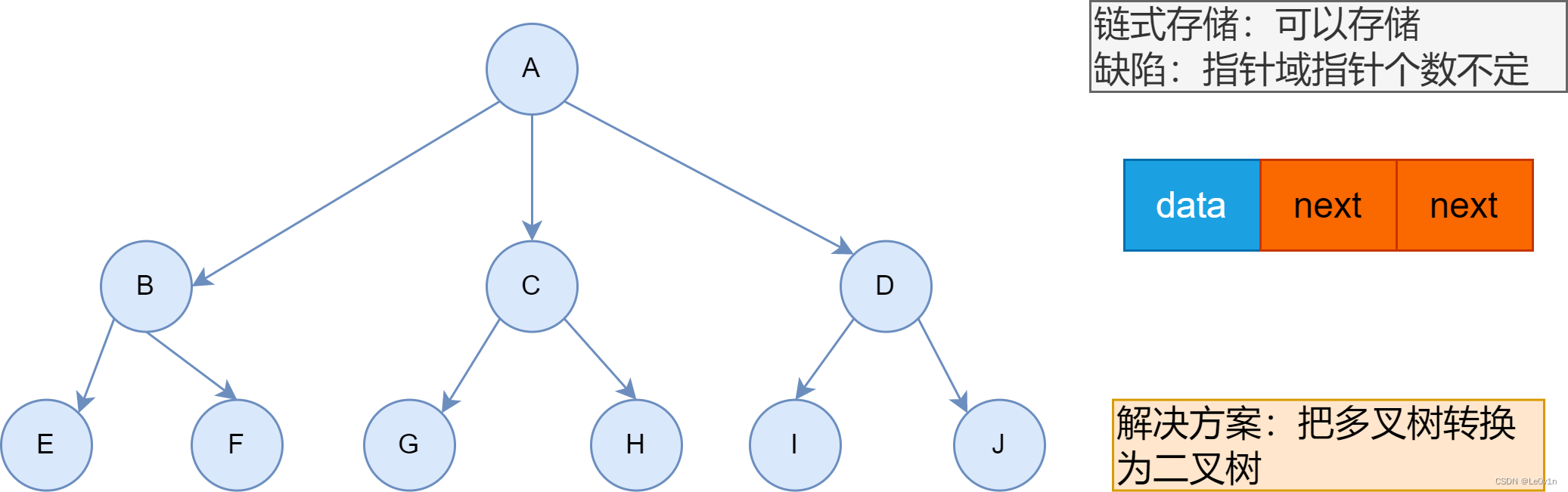
由于对节点的个数无法掌握，常见树的存储表示都转换成二叉树进行处理，子节点个数最多为2。

3. 常见的一些树的应用场景

1. xml，html等，那么编写这些东西的解析器的时候，不可避免用到树
2. 路由协议就是使用了树的算法
3. mysql数据库索引
4. 文件系统的目录结构
5. 所以很多经典的AI算法其实都是树搜索，此外机器学习中的决策树（decision tree）也是树结构

4. 二叉树的基本概念

二叉树是每个节点最多有两个子树的树结构。

通常子树被称作"左子树"(left subtree)和"右子树" (right subtree)。

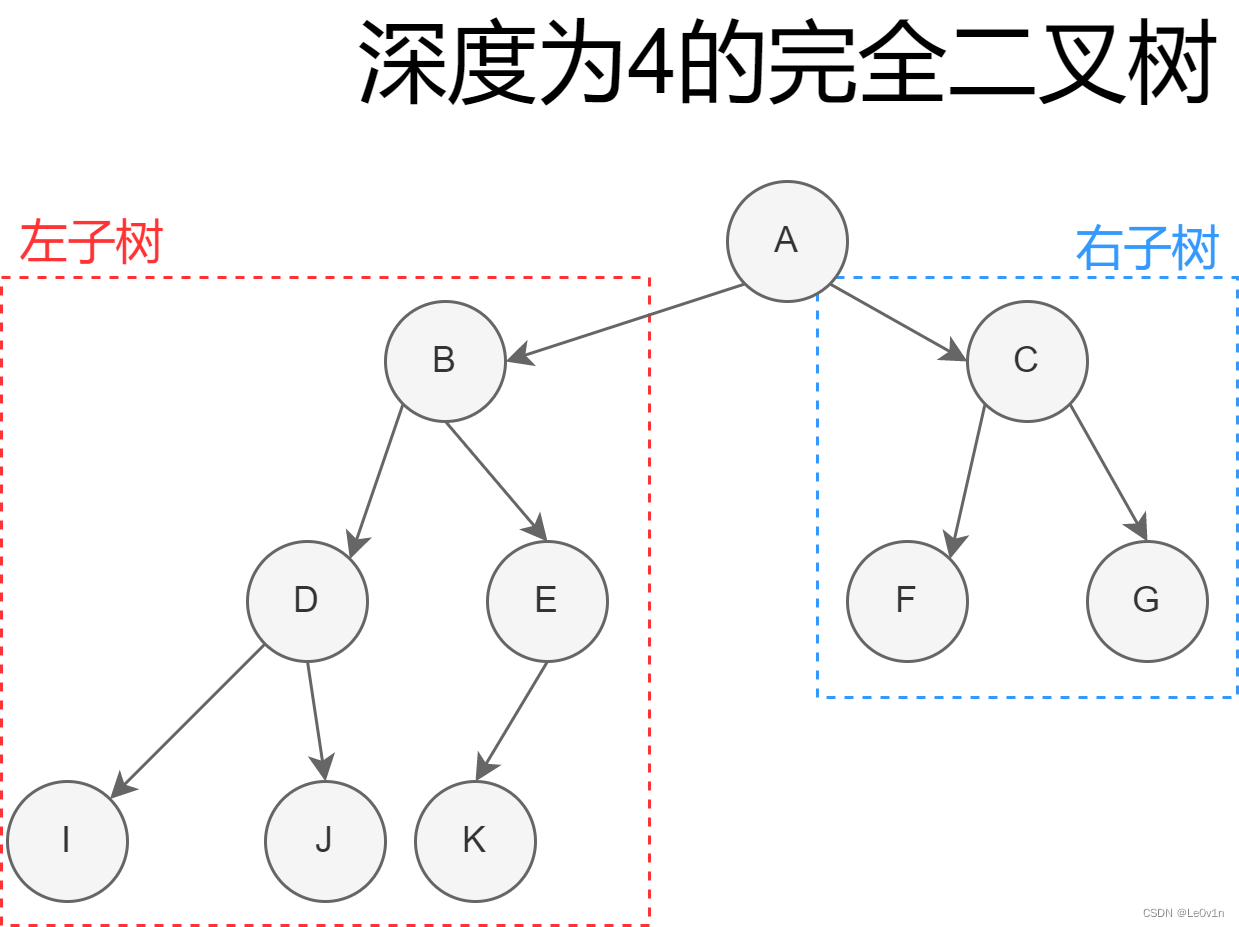
4.1 二叉树的性质（特性）

• 性质1：在二叉树的第 $i$ 层上至多有 $2^{i-1}$ 个结点 $(i>0)$ (根节点只有一个)
• 性质2: 深度为 $k$ 的二叉树至多有 $2^{k-1}$ 个结点 $(k>0)$ (根节点只有一个)
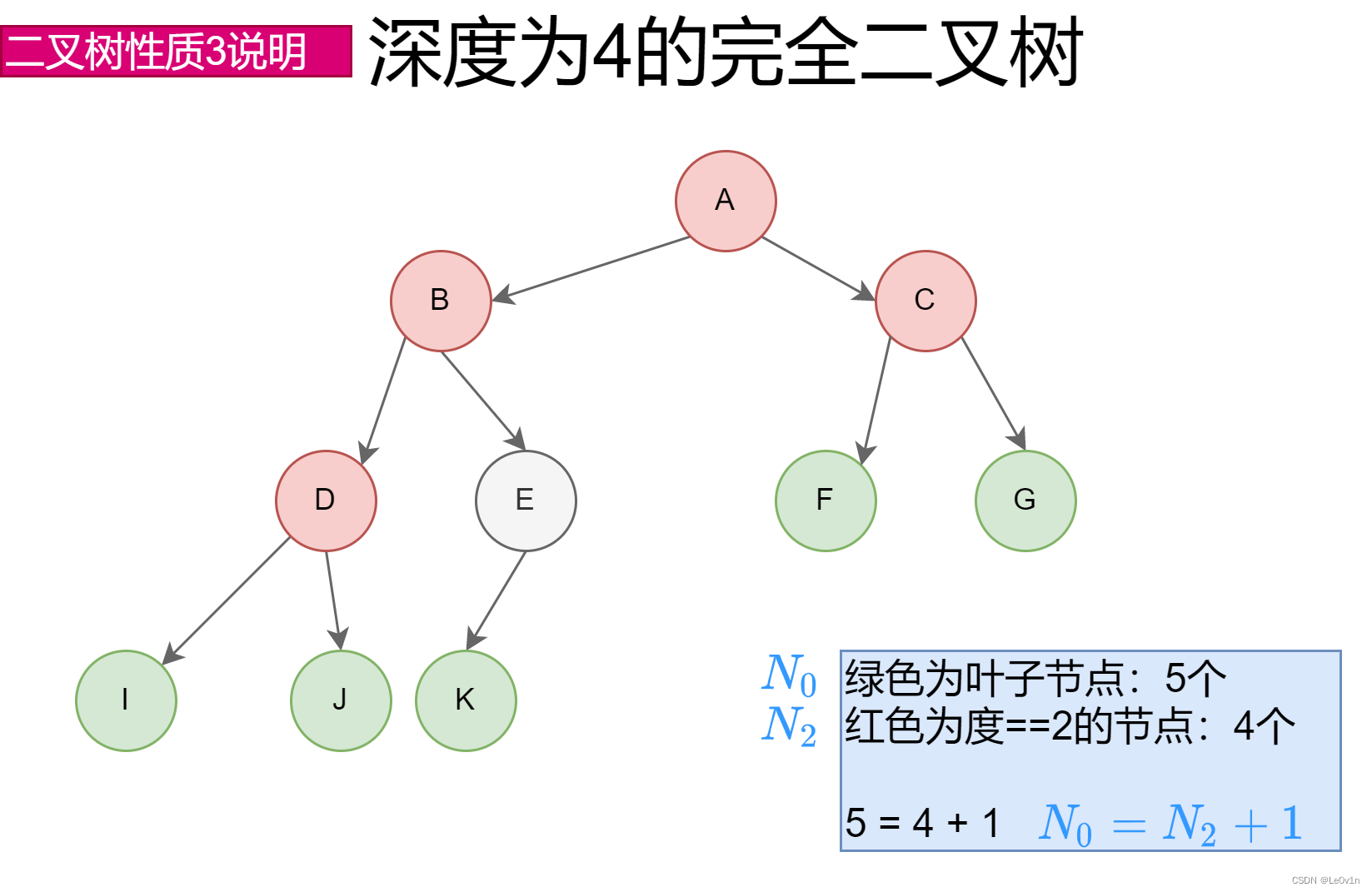
• 性质3: 对于任意一棵二叉树，如果其叶结点数为 $N_0$，而度数为2的结点总数为 $N_2$，则 $N_0=N_2+1$;
• 性质4: 具有n个结点的完全二叉树的深度必为 $lo{g}_2^{(n+1)}$ (和性质2是反着来的，而且这里强调了是完全二叉树)
• 性质5: 对完全二叉树，若从上至下、从左至右编号，则编号为 $i$ 的结点，其左孩子编号必为 $2i$，其右孩子编号必为 $2i+1$；其双亲的编号必为 $\frac{i}{2}$ ($i=1$ 时为根,除外)

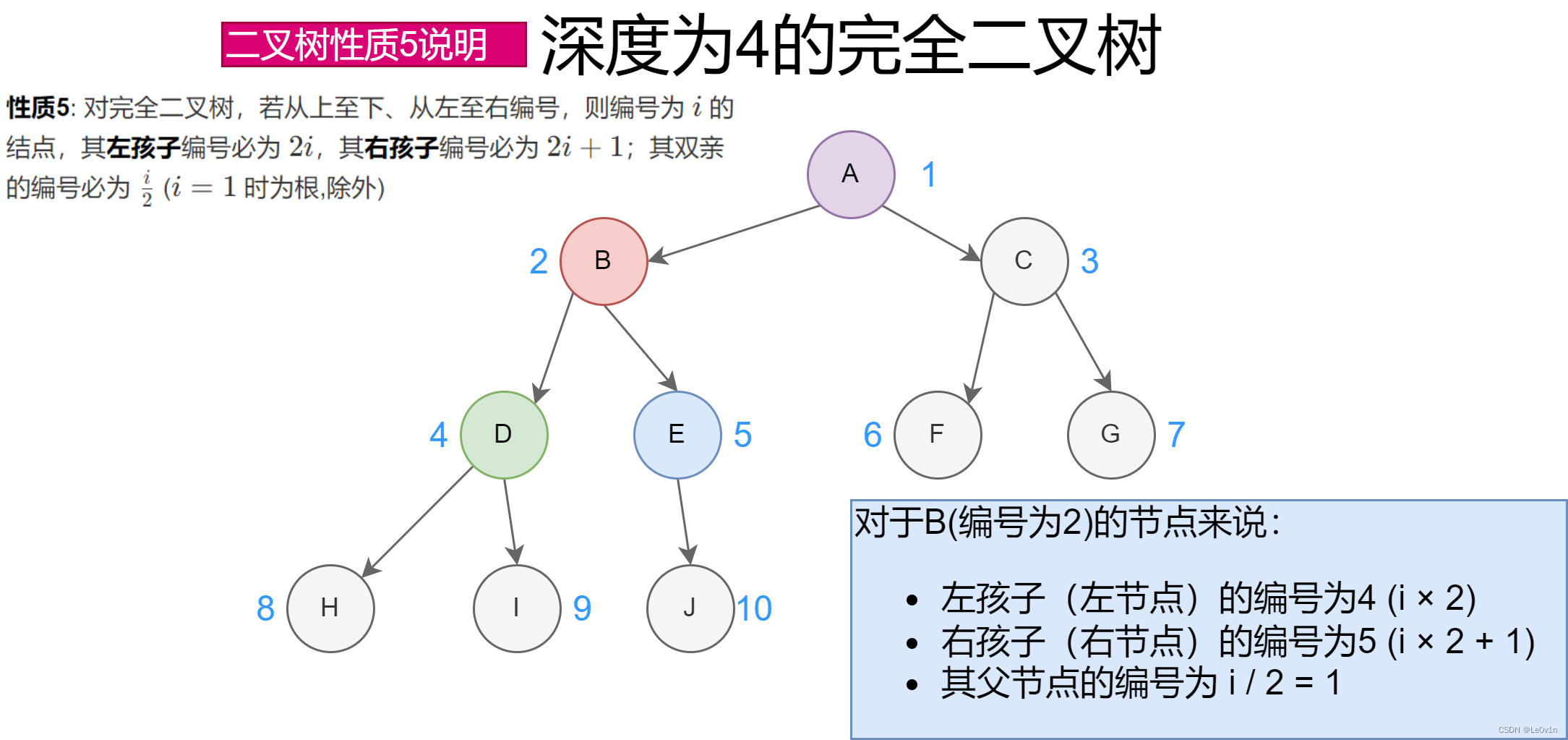
4.2 完全二叉树

完全二叉树——若设二叉树的高度为 $h$，除第 $h$ 层外，其它各层 $(1h-1)$ 的结点数都达到最大个数,第 $h$ 层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

4.3 满二叉树

满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

4.4 平衡二叉树

当且仅当任何节点的两棵子树的高度差不大于1（超过2 -> $le1$）的二叉树;

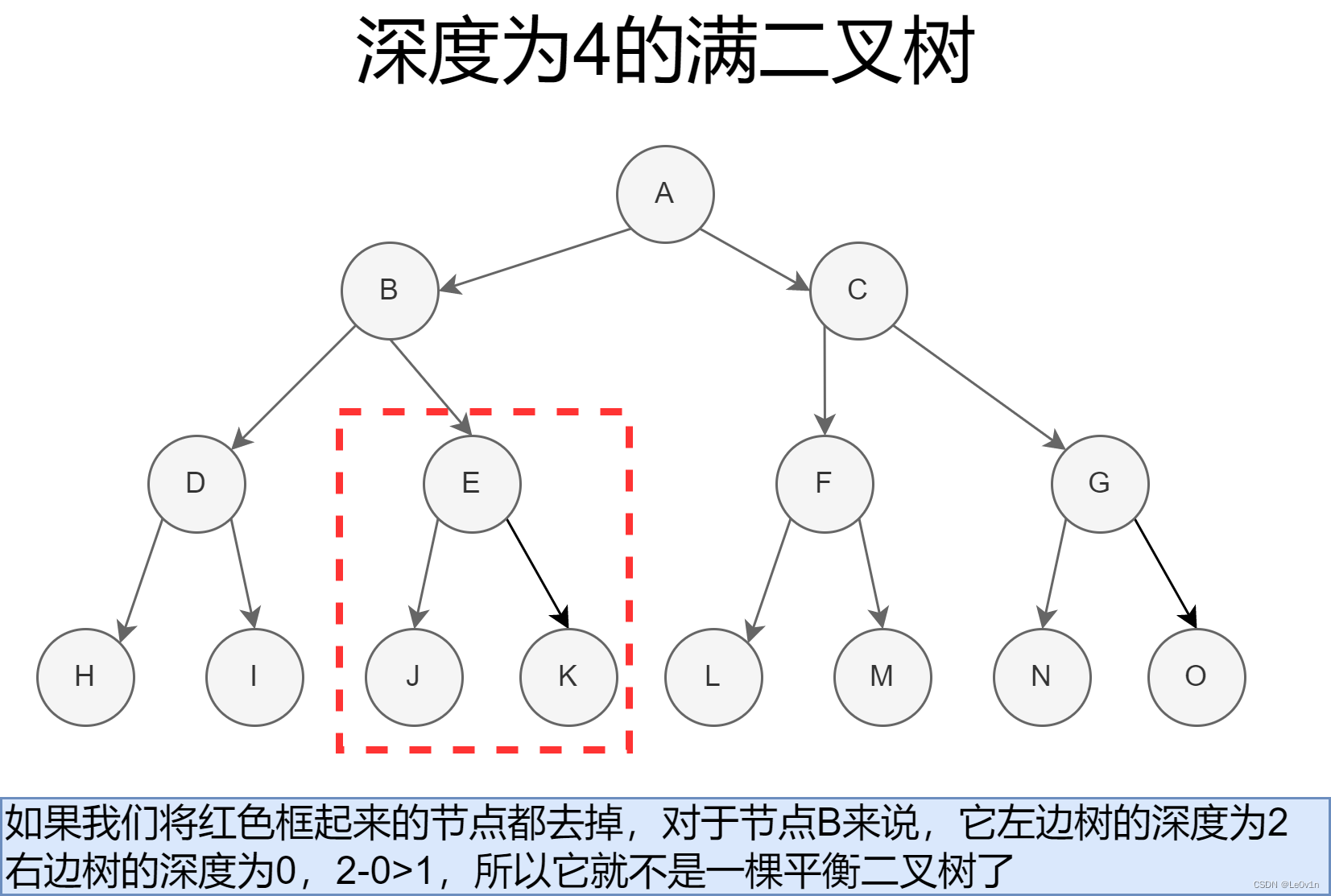
可以看到，平衡二叉树级别没有完全二叉树和满二叉树那么高，它描述的是一种性质。

• 满二叉树和完全二叉树也可以是平衡二叉树
• 平衡二叉树也可以是完全二叉树和满二叉树

4.5 排序二叉树

排序二叉树的结构规则很简单，只遵循一个基本规则：

• 在二叉树中，选择任意根结点，其左子树都比根节点小，右子树都比根节点大

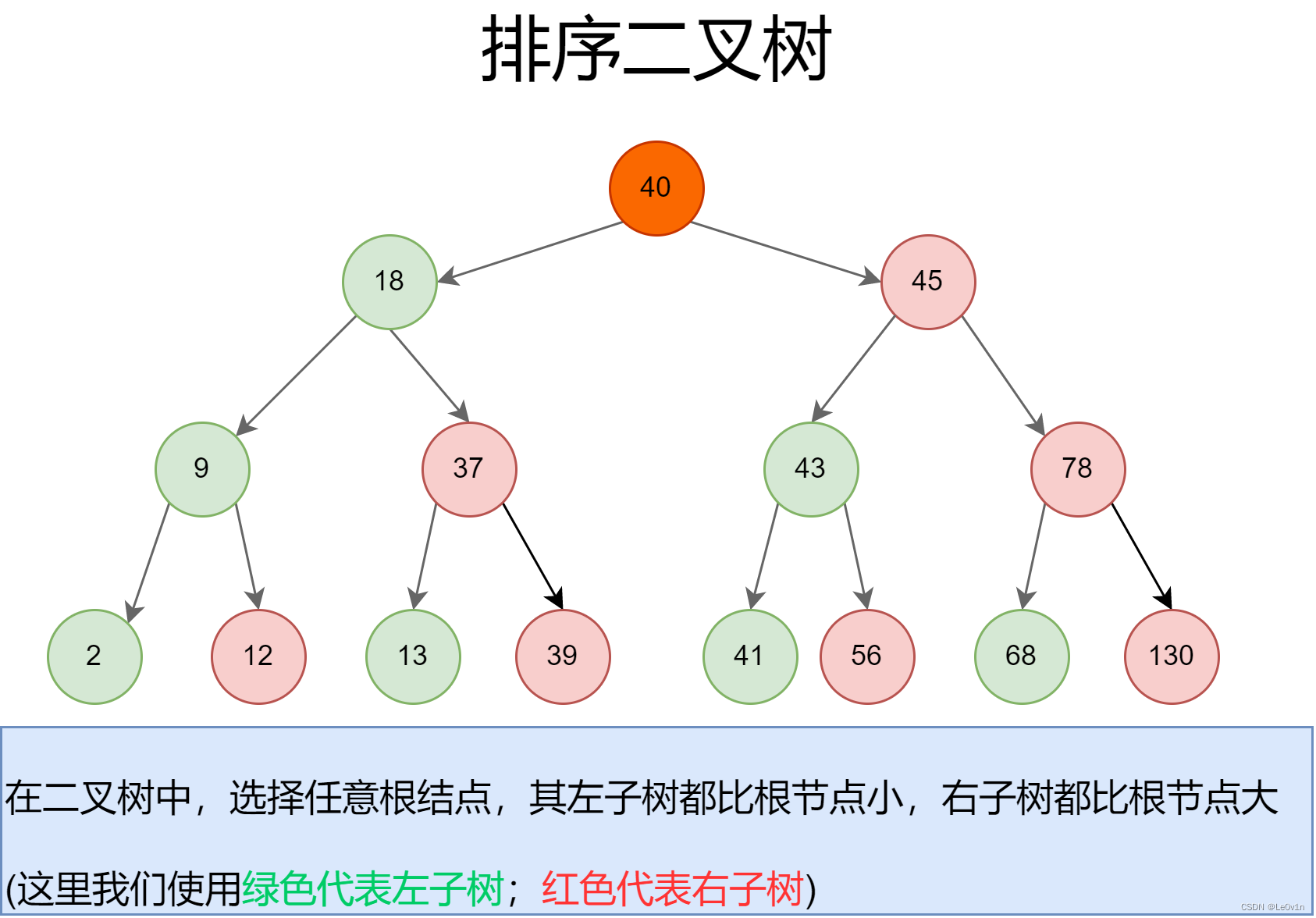
因为这个树非常有规律，且顺序排好了，因此在查找的时候非常方便，过程和二分查找类似。

假设我们需要找39这个数是否存在：

1. 39比40小，在40的左边
2. 39比18大，在18的右边
3. 39比37大，在37的右边
4. 找到39，返回True

5. 二叉树的节点表示以及树的创建

通过使用Node类，定义三个属性：

• elem：节点本身的值
• lchild：左节点
• rchild：右节点

class Node():
    """树的节点"""

    def __init__(self, item):
        self.elem = item  # 需要存储的数
        self.lchild = None  # 左子节点
        self.rchild = None  # 右子节点
1
2
3
4
5
6
7

---

通过使用Tree类，定义根节点即可。

class Tree():
    """二叉树"""

    def __init__(self):
        self.root = None  # 二叉树的根节点
1
2
3
4
5

6. 二叉树添加节点

# coding: utf-8


class Node():
    """树的节点"""

    def __init__(self, item):
        self.elem = item  # 需要存储的数
        self.lchild = None  # 左子节点
        self.rchild = None  # 右子节点


class Tree():
    """二叉树"""

    def __init__(self):
        self.root = None  # 二叉树的根节点

    def add(self, item):
        node = Node(item)  # 先构造一个节点

        if self.root is None:  # 首先判断树是否为空树，如果是空树，则将node链接到root节点即可
            self.root = node
            return

        # 当树不是空树时，开始使用队列进行判断空位置，将新的node链接到空位置上
        queue = []  # 创建一个队列（用来存放需要处理的元素）
        queue.append(self.root)  # 将根节点添加到队列中     这两句话可以简写为 queue = [self.root]

        while queue:  # 只要队列不为空，则一直执行

            cur_node = queue.pop(0)  # 从队头读取数据

            if cur_node.lchild is None:
                cur_node.lchild = node  # 将当前节点链接到这个位置上
                return
            else:
                queue.append(cur_node.lchild)  # 如果有孩子不为空，则将右孩子添加到要处理的队列中
            if cur_node.rchild is None:
                cur_node.rchild = node  # 将当前节点链接到这个位置上
                return
            else:
                queue.append(cur_node.rchild)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

7. 二叉树的遍历

树的遍历是树的一种重要的运算。所谓遍历是指对树中所有节点的信息的访问，即依次对树中每个节点访问一次且仅访问一次，我们把这种对所有节点的访问称为遍历(traversal)。

那么树的两种重要的遍历模式：

1. 深度优先遍历 -> 一般用递归
2. 广度优先遍历 -> 一般用队列

一般情况下能用递归实现的算大部分也能用堆栈来实现。

7.1 深度优先遍历 (纵向遍历) ⭐️

对于一颗二叉树，深度优先搜索(Depth First Search)是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。那么深度遍历有重要的三种方法，这三种方式常被用于访问树的节点，它们之间的不同在于访问每个节点的次序不同。这三种遍历分别叫做：

1. 先序遍历(preorder): 根 -> 左 -> 右
2. 中序遍历（inorder): 左 -> 根 -> 右
3. 后序遍历(postorder): 左 -> 右 -> 根

我们来给出它们的详细定义，然后举例看看它们的应用。

7.1.1 先序遍历(preorder)

在先序遍历中，我们先访问根节点 (root)，然后递归使用先序遍历访问左子树，再递归使用先序遍历访问右子树

---

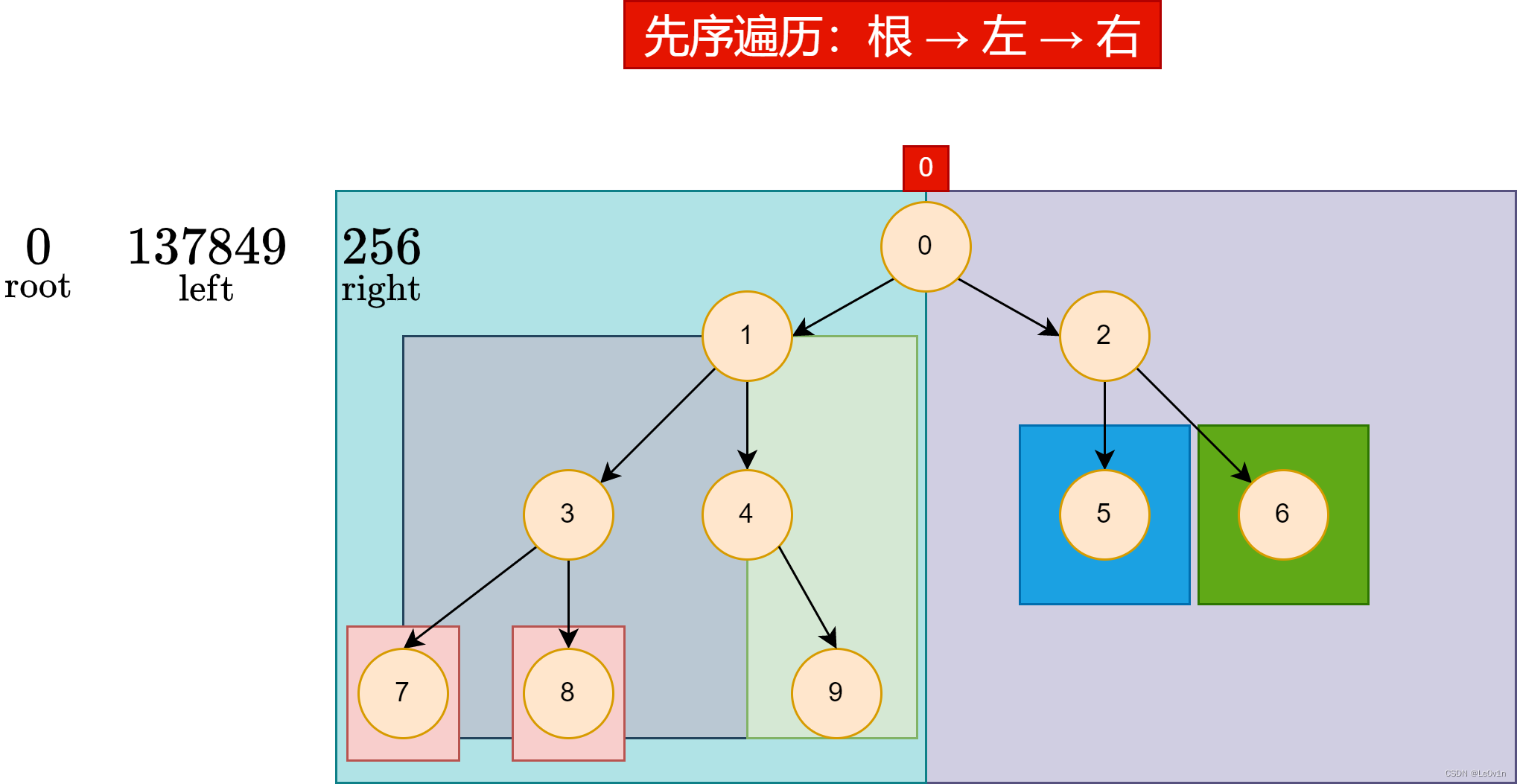
代码实现：

def preorder(self, root):
    """
        使用递归的方式实现先序遍历
            因为设计到了递归，所以我们需要将根和子根传给自身，故有一个root形参
        根 → 左 → 右
    """
    if root is None:  # 递归的终止条件
        return
    
    print(root.elem, end=", ")
    self.preorder(root.lchild)
    self.preorder(root.rchild)
1
2
3
4
5
6
7
8
9
10
11
12

7.1.2 中序遍历

中序遍历在中序遍历中，我们递归使用中序遍历访问左子树，然后访问根节点，最后再递归使用中序遍历访问右子树

左子树 → 根节点 → 右子树

---

代码实现：

def inorder(self, root):
    """
        使用递归的方式实现中序遍历
            因为设计到了递归，所以我们需要将根和子根传给自身，故有一个root形参
        左 → 根 → 右
    """
    if root is None:  # 递归的终止条件
        return
    
    self.inorder(root.lchild)
    print(root.elem, end=", ")
    self.inorder(root.rchild)
1
2
3
4
5
6
7
8
9
10
11
12

7.1.2 后序遍历

后序遍历在后序遍历中，我们先递归使用后序遍历访问左子树和右子树，最后访问根节点

左子树 → 右子树 → 根节点

---

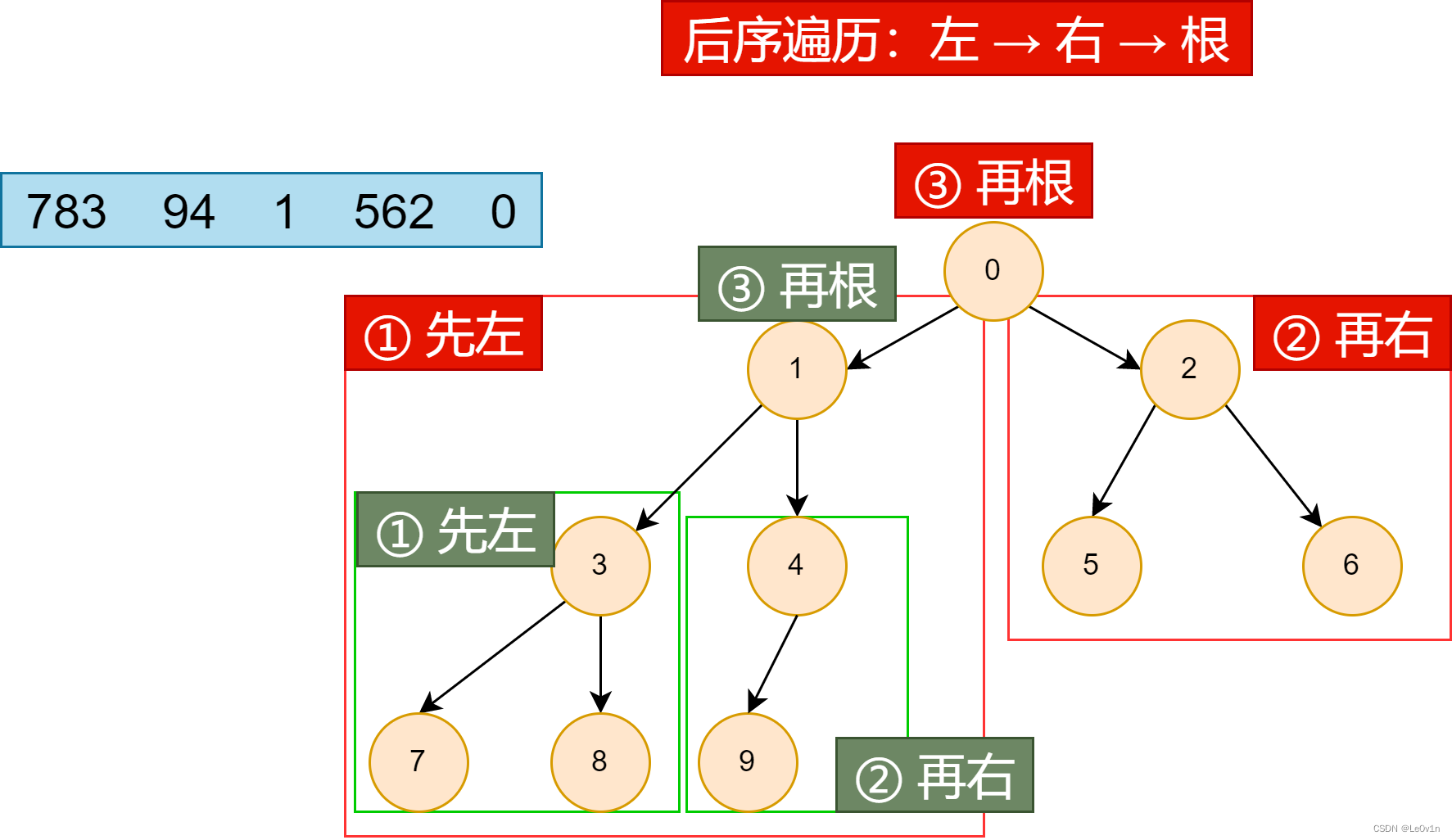
代码实现：

def postorder(self, root):
    """
        使用递归的方式实现后序遍历
            因为设计到了递归，所以我们需要将根和子根传给自身，故有一个root形参
        左 → 右 → 根
    """
    if root is None:  # 递归的终止条件
        return
    
    self.postorder(root.lchild)
    self.postorder(root.rchild)
    print(root.elem, end=", ")
1
2
3
4
5
6
7
8
9
10
11
12

7.2 广度优先遍历 (横向遍历)

从树的root开始，从上到下、从左到右遍历整棵树的节点。

def breadth_travel(self):
    """广度遍历 (思路和add是一样的)
            特殊情况：一开始就是一个空树
    """
    if self.root is None:
        return
    
    queue = [self.root]  # 创建队列并且添加root节点

    print("[", end="")
    while queue:  # 只要队列不为空，则一直执行

        cur_node = queue.pop(0)
        print(cur_node.elem, end=", ")  # 打印当前节点的元素

        if cur_node.lchild:  # 左节点存在
            queue.append(cur_node.lchild)  # 添加到队列中等待处理
        if cur_node.rchild:
            queue.append(cur_node.rchild)  # 添加到队列中等待处理
    print("]", end="\n")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

8. 二叉树：由遍历确定一棵树

---

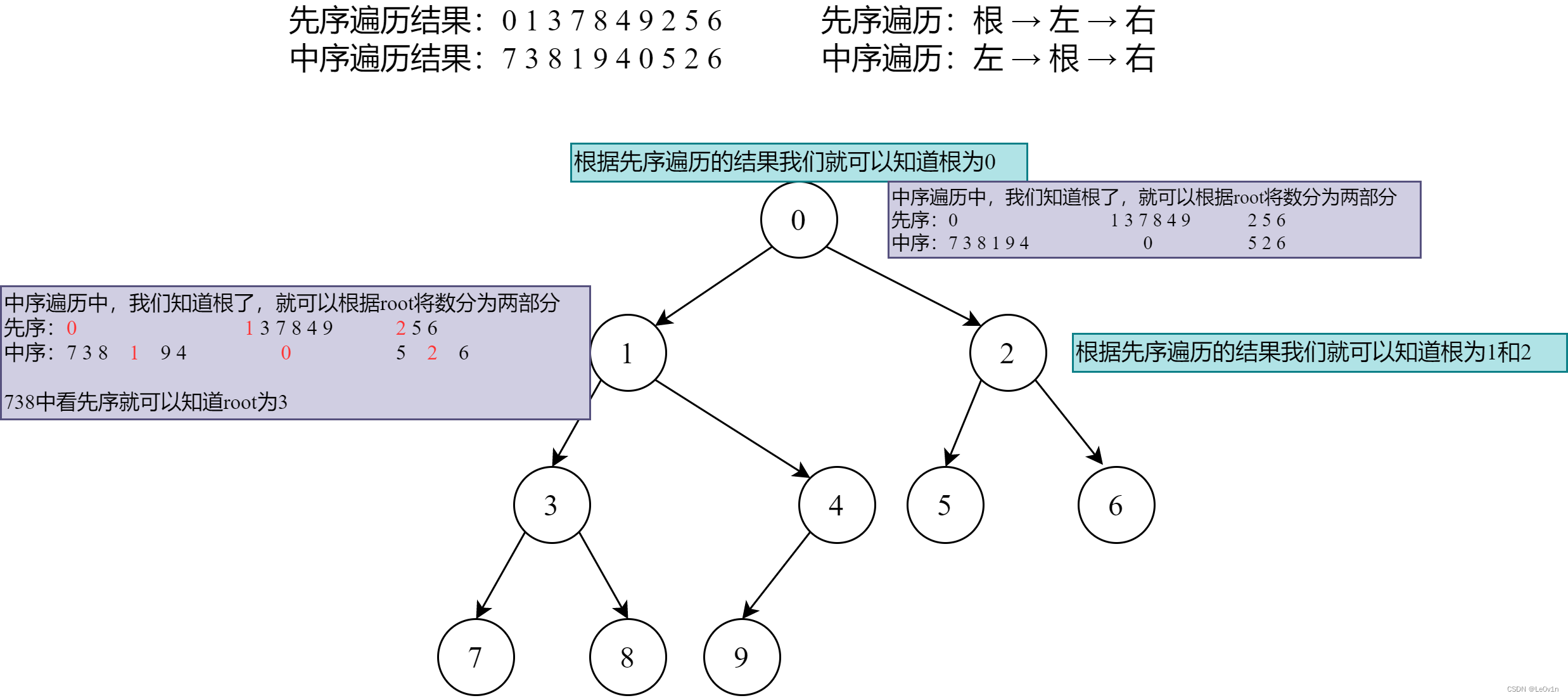
后序：左 右 根
中序：左 根 右

后序结果：7839415620
中序结果：7381940526

首先根据后序的结果我们可以推出root
中序结果：7381940526
       ：738194    0    526

用738194去匹配后序结果中的数字783941，然后找到根1
738194    0    526
738    1     94    0    526

对于738来说，匹配后序结果中的数字783，找到root 3
7 3 8    1     94    0    526

7 3 8已经确定了（根据中序顺序）

我们再看一下94，让它去匹配后序结果中的数字94. root为4
7 3 8    1     9    4    0    526

左 根 右（没有右）

所以94也确定了（左根右）

现在，root 0的左边部分处理完毕了，我们再看右边部分的526

让它去匹配后序结果中的562，根为2

7 3 8    1     9    4    0    5    2    6

正好符合中序顺序（左 根 右）

所以二叉树就确定了（结果和上图是一样的）
 ：738194    0    526

用738194去匹配后序结果中的数字783941，然后找到根1
738194    0    526
738    1     94    0    526

对于738来说，匹配后序结果中的数字783，找到root 3
7 3 8    1     94    0    526

7 3 8已经确定了（根据中序顺序）

我们再看一下94，让它去匹配后序结果中的数字94. root为4
7 3 8    1     9    4    0    526

左 根 右（没有右）

所以94也确定了（左根右）

现在，root 0的左边部分处理完毕了，我们再看右边部分的526

让它去匹配后序结果中的562，根为2

7 3 8    1     9    4    0    5    2    6

正好符合中序顺序（左 根 右）

所以二叉树就确定了（结果和上图是一样的）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62