二分查找

二分查找也常被称为二分法或者折半查找，每次查找时通过将待查找区间分成两部分并只取
一部分继续查找，将查找的复杂度大大减少。对于一个长度为O¹nº 的数组，二分查找的时间复
杂度为$O(logn)$。

二分查找也可以看作双指针的一种特殊情况，但我们一般会将二者区分。双指针类型的题，
指针通常是一步一步移动的，而在二分查找里，指针每次移动半个区间长度。

69. Sqrt(x) (Easy)

题目描述
给定一个非负整数，求它的开方，向下取整。

输入输出样例
输入一个整数，输出一个整数。

Input: 8
Output: 2
8 的开方结果是2:82842:::，向下取整即是2。

思路
使用二分查找，left、right分别指向0和n，每次比较$n$和$mi{d}^2$的关系，mid=(left+right)/2。
如果$n<mi{d}^2$查找范围在前一半，left=mid-1;
如果$n>mi{d}^2$查找范围在后一半, right=mid+1;
如果$n==mi{d}^2$直接返回mid
如果循环结束，则目标值应该在[right,left]两个整数之间
（注意：int可能会值溢出，使用long平方和）

代码

class Solution {
    public int mySqrt(int x) {
        long left=0,right=x;
        while (left<=right){
            long mid = (left+right)/2;
            if(mid*mid>x)right=mid-1;
            else if(mid*mid<x)left=mid+1;
            else return (int)mid;
        }
        return (int)right; //最后没找到的情况，返回值在【right left】中间
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

34. Find First and Last Position of Element in Sorted Array (Medium)

题目描述
给定一个增序的整数数组和一个值，查找该值第一次和最后一次出现的位置。
输入输出样例
输入是一个数组和一个值，输出为该值第一次出现的位置和最后一次出现的位置（从0 开
始）；如果不存在该值，则两个返回值都设为-1。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8 输出：[3,4]
示例 2：
输入：nums = [5,7,7,8,8,10], target = 6 输出：[-1,-1]
示例 3：
输入：nums = [], target = 0 输出：[-1,-1]

思路
就是一个二分查找，找到目标值后，用两个指针分别向两边扩充相同目标值的范围，然后返回该范围。如果二分法没找到，返回[-1,-1]

代码

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int left=0,right=nums.length-1;
        int[] result=new int[2];
        while (left<=right){ //此处可以是等于，相当于指向同一个元素进行后续操作
            int mid = left+(right-left)/2;
            if(nums[mid]<target)left=mid+1;
            else if(nums[mid]>target)right=mid-1;
            else {
                int i = mid,j = mid;
                while (i>=left && nums[i]==nums[mid])i--; //向左扩充，不要超出数组范围
                while (j<=right && nums[j]==nums[mid])j++; //向右扩充
                result[0]=i+1;
                result[1]=j-1;
                return result; //直接返回该范围
            }
        }
        result[0]=-1;
        result[1]=-1;
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

81. Search in Rotated Sorted Array II (Medium)

题目描述
一个原本增序的数组被首尾相连后按某个位置断开（如[1,2,2,3,4,5] ! [2,3,4,5,1,2]，在第一
位和第二位断开），我们称其为旋转数组。给定一个值，判断这个值是否存在于这个为旋转数组
中。
输入输出样例
输入是一个数组和一个值，输出是一个布尔值，表示数组中是否存在该值。

Input: nums = [2,5,6,0,0,1,2], target = 0
Output: true

思路
原本是一个增序数组，断开后两部分仍是增序。使用二分法找到中间位置后，从中间位置分开，有一部分是增序，另一部分不是增序。先判断mid两边哪边是增序，如果是增序：可以判断target是否在该序列中，不在说明在非增序序列中，通过这种方法可以二分找到目标所在的一边。

代码

class Solution {
    public boolean search(int[] nums, int target) {
        int left=0,right=nums.length-1;
        while (left<=right){
            int mid = left+(right-left)/2;
            if(nums[mid] == target) return true;
            if(nums[mid] == nums[left] && nums[mid]==nums[right]){ //如果无法判断target在哪个区间内
                left++; //有重复元素，left右移
            }else { //可以判断在那个区间
                if (nums[right] >= nums[mid]) { //右侧有序
                    if (target > nums[mid] && target <= nums[right]) {//target在右侧
                        left = mid + 1;
                    } else right = mid - 1;
                } else { //左侧有序
                    if (target < nums[mid] && target >= nums[left]) {//target在左侧
                        right = mid - 1;
                    } else left = mid + 1;
                }
            }
        }
        return false;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

154. Find Minimum in Rotated Sorted Array II (Medium)

问题描述
已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,4]
若旋转 7 次，则可以得到 [0,1,4,4,5,6,7]
注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

给你一个可能存在 重复 元素值的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须尽可能减少整个过程的操作步骤。

输入输出样例
示例 1：

输入：nums = [1,3,5]
输出：1

示例 2：

输入：nums = [2,2,2,0,1]
输出：0

思路
该数组之前是一个递增数组，只是经过了旋转。由此，可以通过二分法找到mid元素，mid元素肯定一边有序，一边无序。可以通过nums[mid]<=nums[right]判断有序的一边是否在右侧，反之在左侧。在有序的一侧，最小值为最左边的元素。之后在右侧找是否存在更小的元素。

代码

class Solution {
    public int findMin(int[] nums) {
        int left=0,right=nums.length-1;
        int min = Integer.MAX_VALUE;
        while (left<=right){
            int mid = (left+right)/2;
            min = Math.min(min,nums[mid]);
            min = Math.min(min,nums[left]);
            min = Math.min(min,nums[right]);
            if(nums[left]==nums[mid] && nums[mid]==nums[right]){ //无法判断哪边是有序
                left++;
            }else { //可以判断哪边是有序的
                if(nums[mid]<=nums[right]){//右边是有序的
                    min=Math.min(min,nums[mid]); //则右边第一个是最小的
                    right=mid-1; //继续去左边寻找
                }else { //左边是有序的
                    min=Math.min(min,nums[left]);
                    left=mid+1; //去右边寻找是否有更小值
                }
            }
        }
        return min;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

540. Single Element in a Sorted Array (Medium)

问题描述
给你一个仅由整数组成的有序数组，其中每个元素都会出现两次，唯有一个数只会出现一次。

请你找出并返回只出现一次的那个数。

你设计的解决方案必须满足 O(log n) 时间复杂度和 O(1) 空间复杂度。

示例 1:

输入: nums = [1,1,2,3,3,4,4,8,8]
输出: 2

示例 2:

输入: nums = [3,3,7,7,10,11,11]
输出: 10

思路
因为数组是有序的，于是可以用二分查找到mid元素。如果mid是奇数，则当nums[mid]==nums[mid+1]时可以判断该单数在左侧；如果mid是偶数，则当nums[mid]!=nums[mid+1]时可以判断该单数在左侧。否则就在右侧。

代码

class Solution {
    public int singleNonDuplicate(int[] nums) {
        int left=0,right=nums.length-1;
        if(nums.length==1)return nums[0];
        while (left<=right){
            int mid = (left+right)/2;
            if((mid==0 && nums[mid]!=nums[mid+1]) || (mid==nums.length-1 && nums[mid]!=nums[mid-1])||( nums[mid]!=nums[mid+1]&& nums[mid]!=nums[mid-1]) )return nums[mid];
            //判断该单值在左侧还是在右侧
            if(mid%2==0 && nums[mid]!=nums[mid+1] || mid%2==1 && nums[mid]==nums[mid+1]){//该单值在左侧
                right=mid-1;
            }else left=mid+1; 
        }
        return -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

4. Median of Two Sorted Arrays (Hard)

问题描述
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

输入输出样例
示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

思路
方法一：将两个无序数组合并成一个有序数组，然后找这个有序数组的中位数
方法二：将从两个有序数组中找中位数的问题转换为，在两个有序数组中找第k大的数字num。该方法原理是：将两个数组从k/2-1位置分别分成两部分，然后比较A[k/2-1]和B[k/2-1]，小的元素所在数组[0，k/2]位置不可能存在第k个大小，可以删除。之后新的数组中重新找第k-k/2大小的元素。直到k==1时，剩余两个数组中，首元素小的就是最初要找的num。（在实际代码中，需要考虑如果其中一个数组较短，k取值可能越界问题）

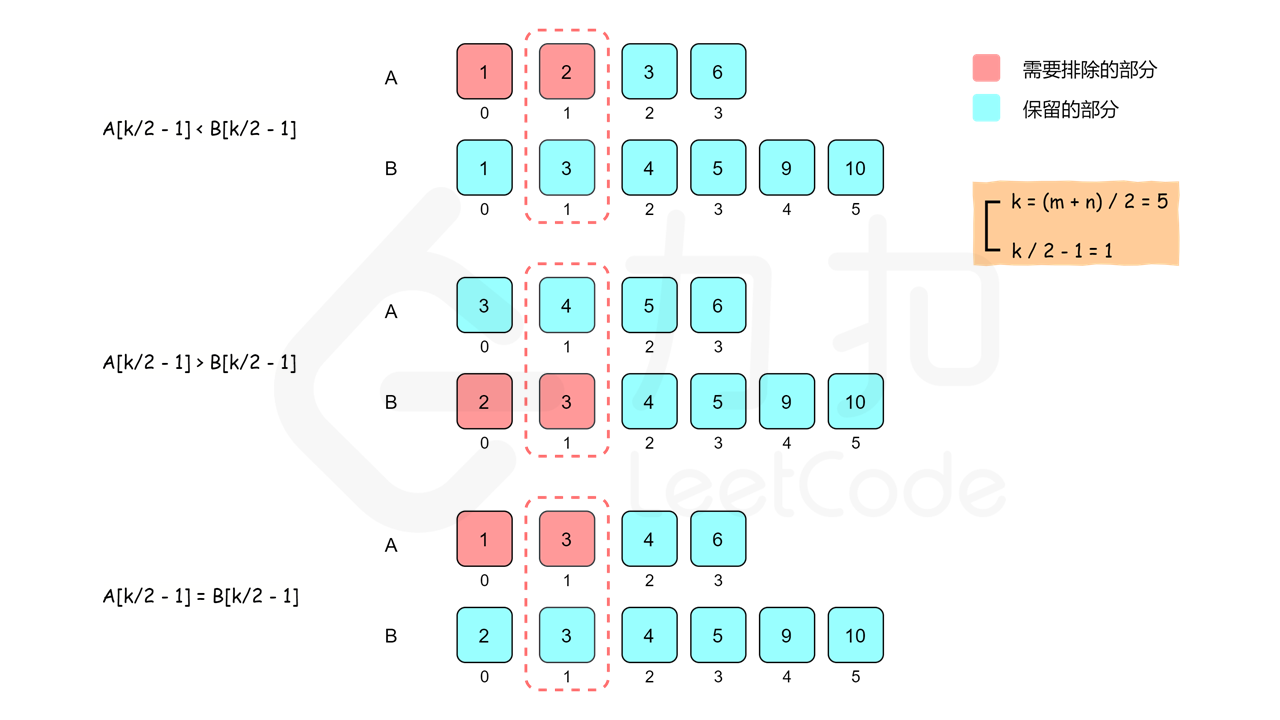
代码

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        //相当于是找第(nums1.length+nums2.length)/2大小的数
        boolean isO = (nums1.length+nums2.length)%2==0;
        if(isO){ //偶数
            int left = findKSortedArrays(nums1,nums2,(nums1.length+nums2.length+1)/2);
            int right = findKSortedArrays(nums1,nums2,(nums1.length+nums2.length+1)/2+1);
            return (left+right)/2.0;
        }else //奇数
            return findKSortedArrays(nums1,nums2,(nums1.length+nums2.length+1)/2);

    }

    public int findKSortedArrays(int[] nums1, int[] nums2,int k){//寻找第k大的数
        int i=0,j=0;
        int len1=nums1.length,len2=nums2.length;
        while (k>1){
            int left=k/2; //每次要删除的区间大小
            //当其中一个数组删除变为空时，直接从另一个数组中找第k大小的元素
            if(len1==0) return nums2[k+j-1];       
            if(len2==0) return nums1[k+i-1];
            //存在一个数组过长，一个数组短的情况，直接使用left作为删除区间，短的数组会越界
            //于是把left范围缩到合适位置
            left = Math.min(left,len1);
            left = Math.min(left,len2);
            //每次比较待删除区域的后一个元素，i,j每次指向删除区域后数组的第一个元素
            if(nums1[i+left-1]<=nums2[j+left-1]) { //删除nums1的[i,left]区域
                i = i+left;
                len1-=left;
            }
            else { //删除nums1的[i,left]区域
                j = j+left;
                len2-=left;
            }
            k = k - left;//删除之后，变为寻找第k-left大小的元素
        }
        //当k==1时，可能存在nums1[i]或nums2[j]越界的情况
        if(len1==0) return nums2[k+j-1];       
        if(len2==0) return nums1[k+i-1];
        return Math.min(nums1[i],nums2[j]);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42