数论

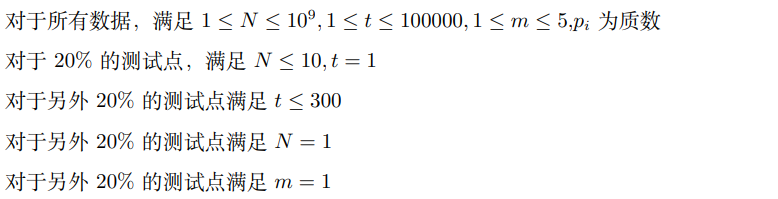
题解

容易发现发现我们的$F$是一个积性函数，显然，组成它的$\varphi$都是积性的，它们于是卷起来的，$F$肯定是积性的。
所以我们的$G(N)={\sum }_{\sum k_i=N}\prod F(p_i^{k_i})$，但这样好像不是特别好看的样子，我们可以考虑转化成生成函数的形式。
我们定义$F_i={\sum }_{j=0}^{\infty }F(p_i^j)x^j$，容易发现，
$$\begin{gathered} F_i=(\sum _{j=0}^{\infty }\varphi (p_i^j)x^j{)}^m=(1+\sum _{j=1}^{\infty }(p_i^j-p_i^{j-1})x^j{)}^m=(\frac{1-x}{1-p_{i}x}{)}^m \\ G(N)=[x^N]\prod _{i=1}^t{F}_i=[x^N]\prod _{i=1}^t{\left(\frac{1-x}{1-p_{i}x}\right)}^m \end{gathered}$$现在我们的目的是计算这个分式的第$N$项，显然$N$这么大，不太可能暴力乘出来。
一种较为常见的计算分式远项的方法是线性递推，我们把上面的式子化一化，
也就是将原来的分式简单变化一下$F=\frac{g(x)}{f(x)}=\frac{f(-x)g(x)}{f(-x)f(x)}=\frac{g^{\prime }(x)}{f^{\prime }(x^2)}$，这样的话，下面就只剩下偶数次项了。
如果我们要求的是第$N$项的$N$为偶数，那么上面的$g^{\prime }(x)$就只有偶数项有用，递归到，同样$N$为奇数，上面也只有奇数项有用。
可以尝试递归求解，
[ x N ] g ( x ) f ( x ) = { [ x N 2 ] f e v e n ′ ( x ) g ′ ( x ) ( 2 ∣ N ) [ x N − 1 2 ] f o d d ′ ( x ) g ′ ( x ) ( 2 ∤ N ) [x^N]\frac{g(x)}{f(x)}=\left\{

\\\right. [xN]f(x)g(x)​={[x2N​]g′(x)feven′​(x)​[x2N−1​]g′(x)fodd′​(x)​​(2∣N)(2∤N)​每次递归相当于都要做一次多项式乘法，将$f$与$g$变成$f^{\prime }$和$g^{\prime }$，同时将$N$除以二。
直到我们的$N$变为$0$，这时候我们的答案就是$\frac{[x^0]G(x)}{[x^0]F(x)}$了。

时间复杂度$O\left(mt\log n\log t\right)$

源码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
typedef unsigned int uint;
#define MAXN 500005
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
const LL INF=0x3f3f3f3f3f3f3f3f;
const int mo=998244353;
const int orG=3,ivG=332748118;
template<typename _T>
void read(_T &x){
   _T f=1;x=0;char s=getchar();
   while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
   while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
   x*=f;
}
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
LL gcd(LL a,LL b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,t,m,p[MAXN],ff[MAXN],Cg[10][10],f[MAXN],g[MAXN];
int F[MAXN<<2],G[MAXN<<2],H[MAXN<<2],rev[MAXN<<2];
void init(){
    ff[1]=1;for(int i=2;i<=m*t;i++)ff[i]=1ll*(mo-mo/i)*ff[mo%i]%mo;
    for(int i=0;i<=m;i++){
        Cg[i][0]=Cg[i][i]=1;
        for(int j=1;j<i;j++)
            Cg[i][j]=add(Cg[i-1][j-1],Cg[i-1][j],mo);
    }
}
void NTT(int *A,const int lim,const int typ){
    for(int i=0;i<lim;i++)if(i<rev[i])swap(A[i],A[rev[i]]);
    for(int mid=1;mid<lim;mid<<=1){
        const int W=qkpow(typ^1?ivG:orG,(mo-1)/(mid<<1),mo);
        for(int i=mid<<1,j=0;j<lim;j+=i)
            for(int Wn=1,k=j;k<j+mid;k++,Wn=1ll*W*Wn%mo){
                int x=A[k],y=1ll*Wn*A[k+mid]%mo;
                A[k]=add(x,y,mo);A[k+mid]=add(x,mo-y,mo);
            }
    }
    if(typ^-1)return ;int tp=qkpow(lim,mo-2,mo);
    for(int i=0;i<lim;i++)A[i]=1ll*tp*A[i]%mo;
}
void sakura(int l,int r){
    if(l==r){
        for(int i=1,now=1;i<=m;i++)
            now=1ll*(mo-p[l])*now%mo,
            f[i+(l-1)*m]=1ll*Cg[m][i]*now%mo;
        return ;
    }
    int mid=l+r>>1;sakura(l,mid);sakura(mid+1,r);
    int lim=1,L=0;while(lim<=(r-l+1)*m)lim<<=1,L++;
    for(int i=0;i<lim;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<L-1);
    for(int i=1;i<=(mid-l+1)*m;i++)F[i]=f[i+(l-1)*m];F[0]=1;NTT(F,lim,1);
    for(int i=1;i<=(r-mid)*m;i++)G[i]=f[i+mid*m];G[0]=1;NTT(G,lim,1);
    for(int i=0;i<lim;i++)F[i]=1ll*F[i]*G[i]%mo;NTT(F,lim,-1);
    for(int i=1;i<=(r-l+1)*m;i++)f[i+(l-1)*m]=F[i];
    for(int i=0;i<lim;i++)F[i]=G[i]=0;
}
int main(){
    //freopen("math.in","r",stdin);
    //freopen("math.out","w",stdout);
    read(n);read(t);read(m);init();
    for(int i=1;i<=t;i++)read(p[i]);f[0]=1;sakura(1,t);
    for(int i=0,now=1;i<=m*t;i++)
        g[i]=(i&1)?mo-now:now,now=1ll*(m*t-i)*ff[i+1]%mo*now%mo;
    int lim=1,L=0;while(lim<=2*m*t)lim<<=1,L++;
    for(int i=0;i<lim;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<L-1);
    while(n){
        for(int i=0;i<=m*t;i++)F[i]=f[i],H[i]=(i&1)?mo-f[i]:f[i],G[i]=g[i],f[i]=g[i]=0;
        NTT(F,lim,1);NTT(G,lim,1);NTT(H,lim,1);
        for(int i=0;i<lim;i++)F[i]=1ll*F[i]*H[i]%mo;NTT(F,lim,-1);
        for(int i=0;i<lim;i++)G[i]=1ll*G[i]*H[i]%mo;NTT(G,lim,-1);
        for(int i=0;i<=2*m*t;i+=2)f[i>>1]=F[i];
        for(int i=n&1;i<=2*m*t;i+=2)g[i>>1]=G[i];
        for(int i=0;i<lim;i++)F[i]=G[i]=H[i]=0;n>>=1;
    }
    printf("%lld\n",1ll*g[0]*qkpow(f[0],mo-2,mo)%mo);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

谢谢！！！