Leetcode1-两数之和详解

Leetcode2-两数相加详解

Leetcode20-有效的括号详解

Leetcode21-合并两个有序链表详解

---

目录

题目

示例

解析

回溯法

代码

python代码

Java代码

---

题目

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

让我们来分析一下题目：

已知：生成括号的对数n

目标：设计函数生成有效括号

要求：输出所有有效括号组合（字符串）

示例

示例1

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例2

输入：n = 1
输出：["()"]

解析

回溯法

针对这个题目，我们已知的是括号的对数，例如2对括号，那么2对括号就对应2个左括号和2个右括号，这4个括号就有6种不同的排列组合，但是这6中排列组合中并不是所有组合都有效，所以我们可以用回溯法量所有组合进行排列，在排列的过程中进行有效性判断。

让我们详细说明一下

如下图所示，对于2对括号会有2个左括号和2个右括号

对于这四个括号共有6中不同的排列组合，其中虚线框中为剩余的括号，这6种排列组合中只有2中是有效的

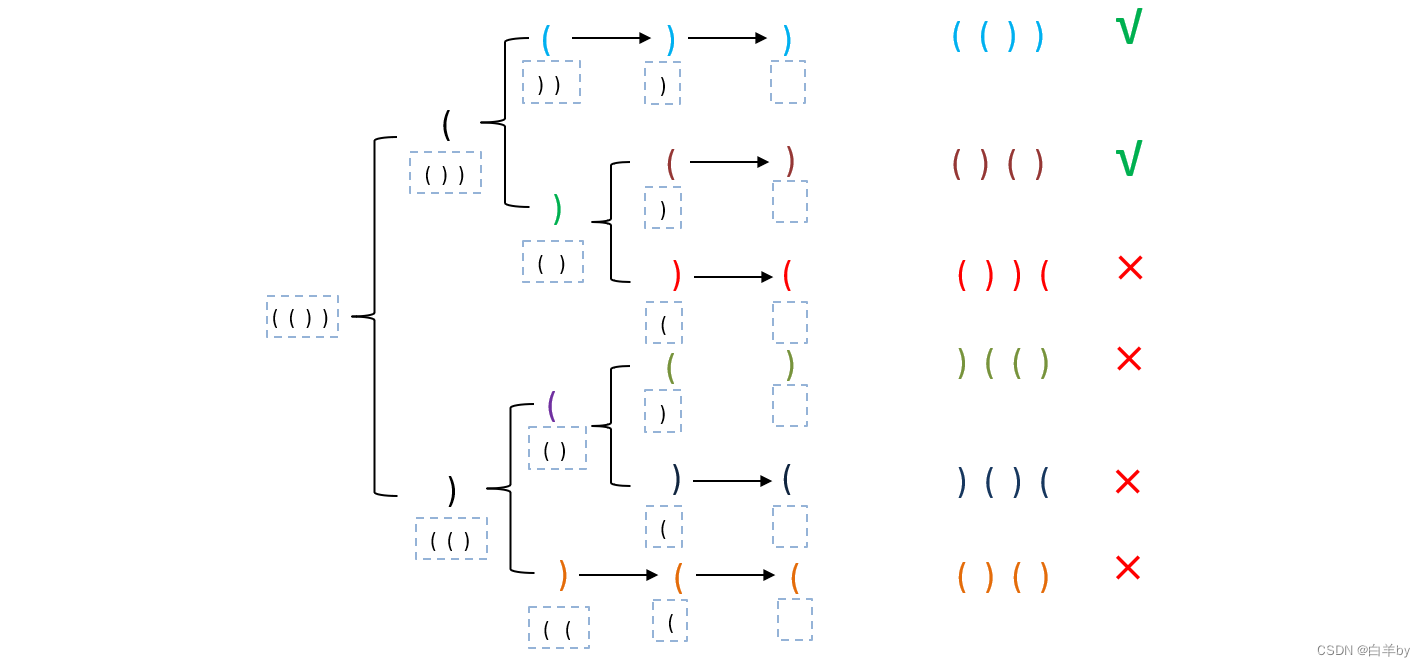
我们知道当遇到一个右括号时，它前面必须要有一个左括号与之对应，即左括号的数量要值大于或等于右括号的数量（l >= r），如果左括号的数量小于右括号的数量，则必有一个右括号没有与之对应的左括号，让我们对每一种排列组合详细看一下有效或无效的原因

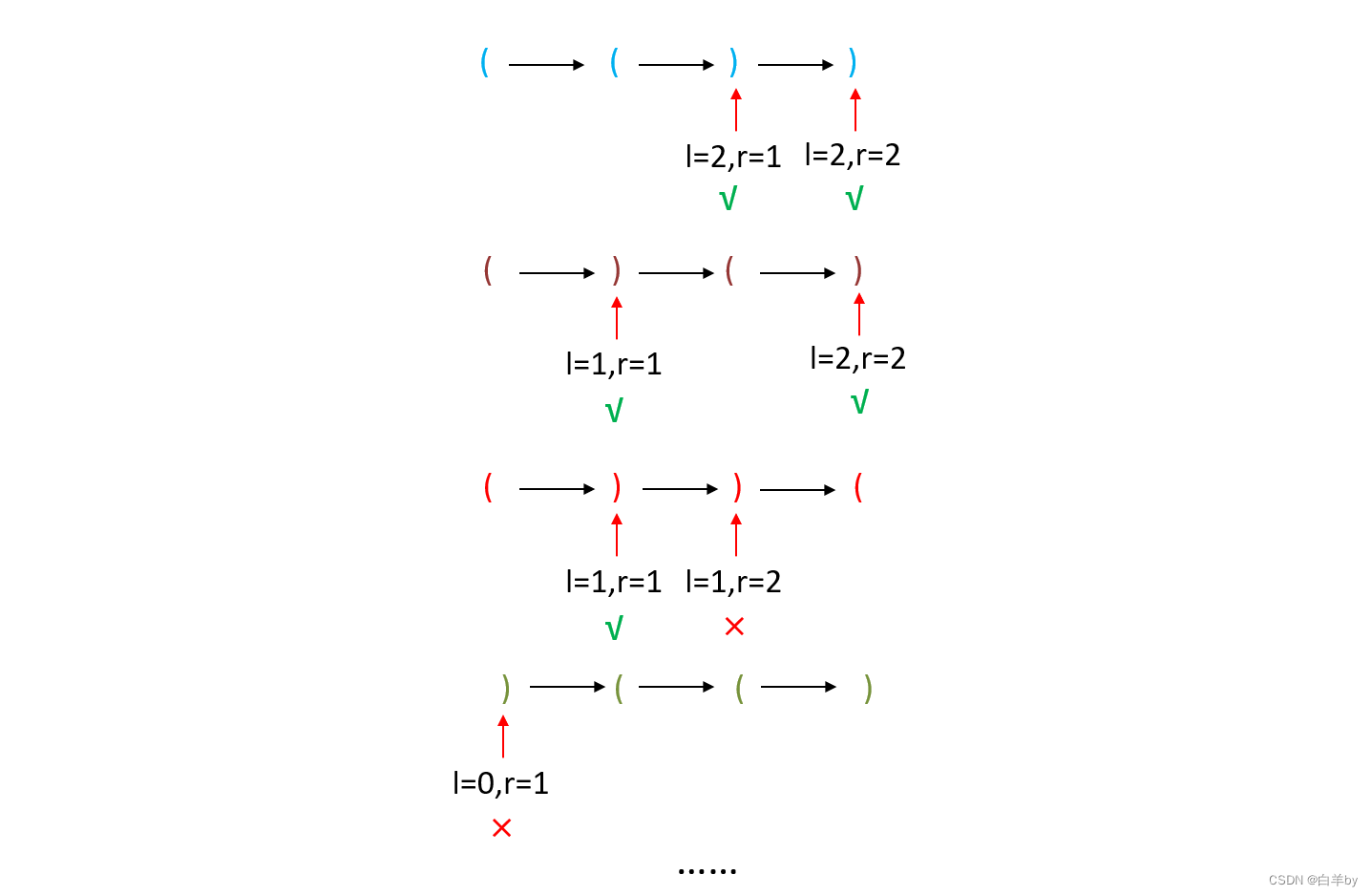
代码

python代码

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        result = []  # 建立列表，保存最后有效的括号组合
        self.backtracking(n, result, 0, 0, "")  # 调用backtracking进行排列组合和有效判定，舒适化左右括号数量为0
        return result
 
    def backtracking(self, n, result, left, right, s):
        if left < right:  # 当左括号数量小于右括号数量时，无效
            return
 
        if (left == n and right==n):
            result.append(s)
            return
 
        if left < n: # 当左括号数量有剩余时，添加左括号，进行回溯
            backtracking(n, result, left+1, right, s+"(")
 
        if right <n:
            backtracking(n, result, left, right+1, s+")")  # # 当右括号数量有剩余时，添加左括号，进行回溯

只看代码的话可能有些难以理解，让我们来看一些怎么回溯的

首先窗帘一个空列表，然后开始进入递归

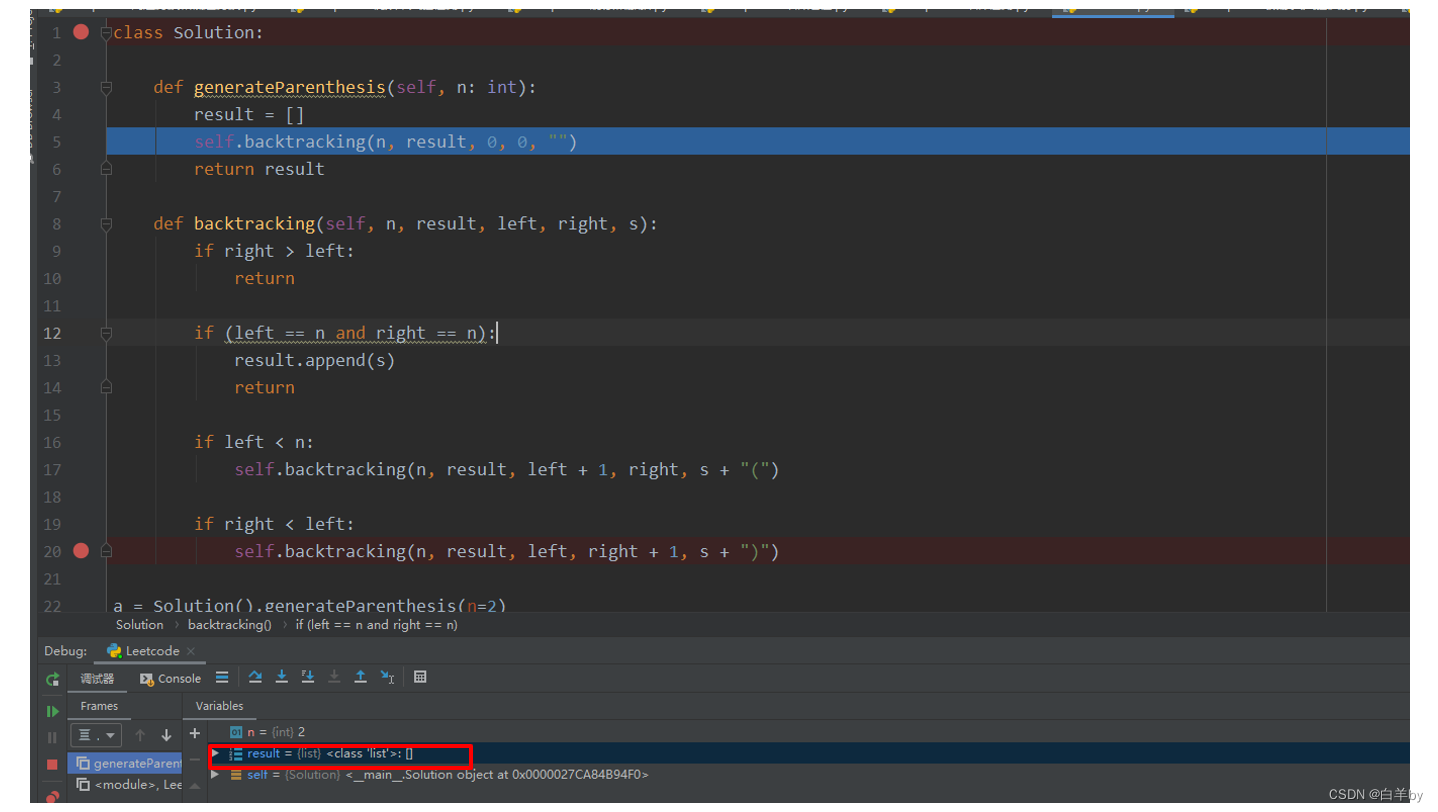
首先得到的第一个组合“(())”

 

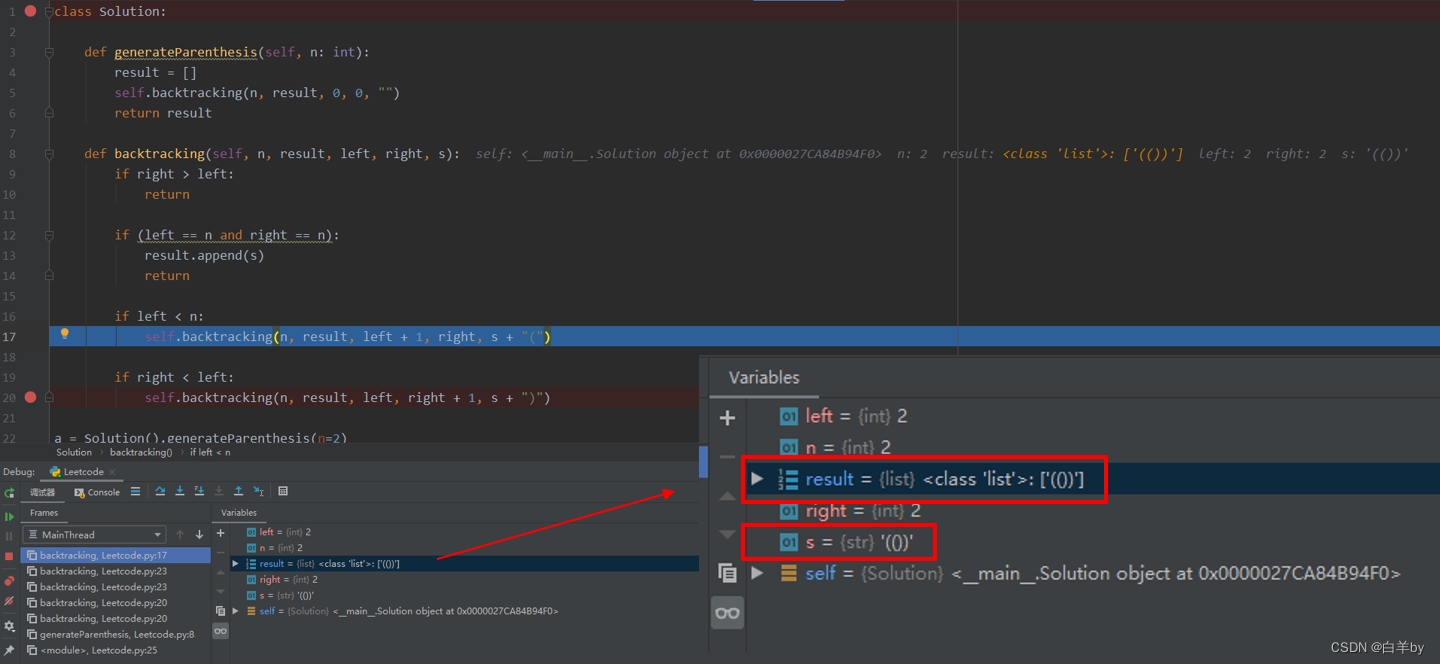
然后从这里人开始回溯，从“(”又开始组合

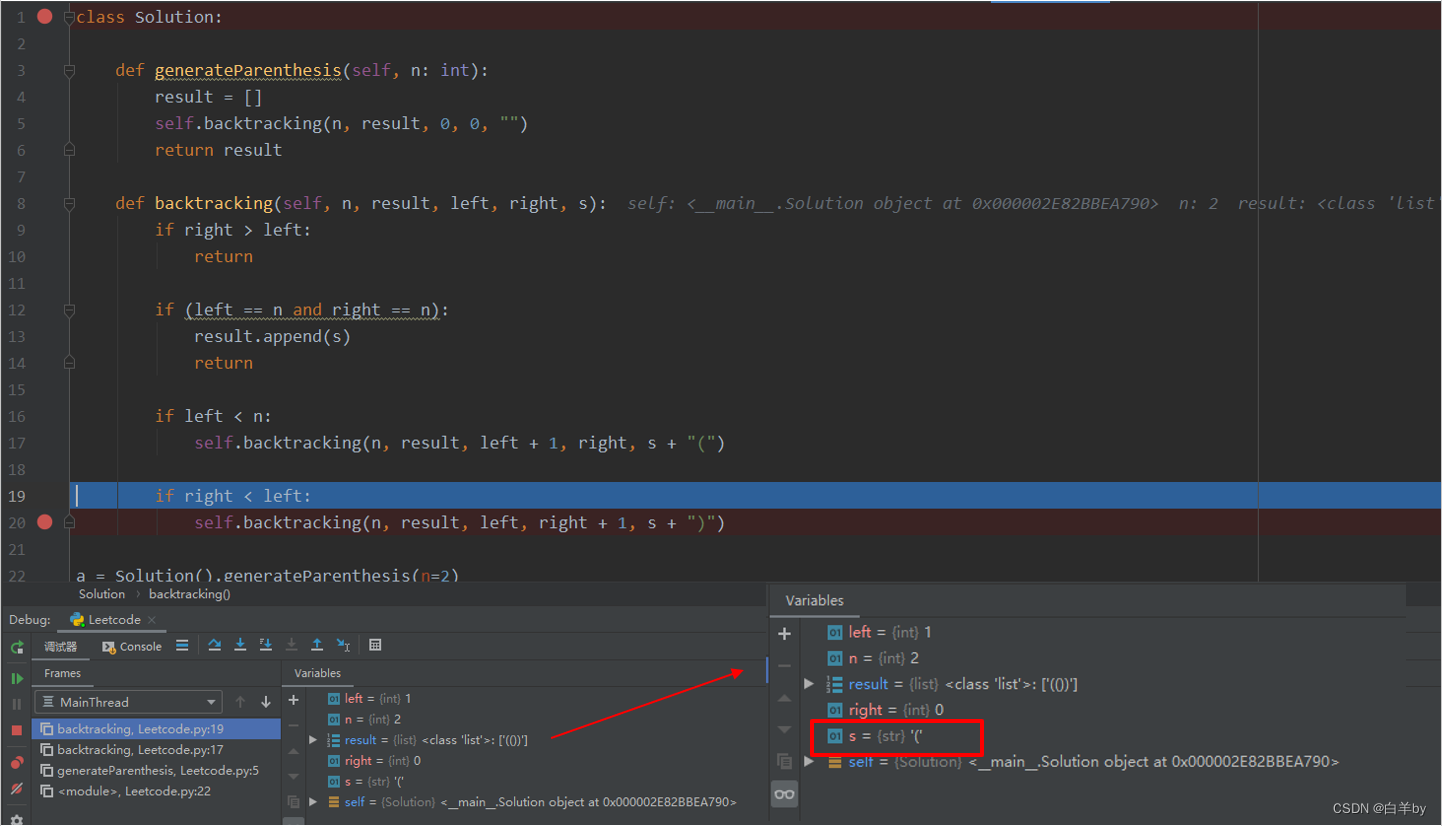
 得到有一个有效的组合“()()”

 

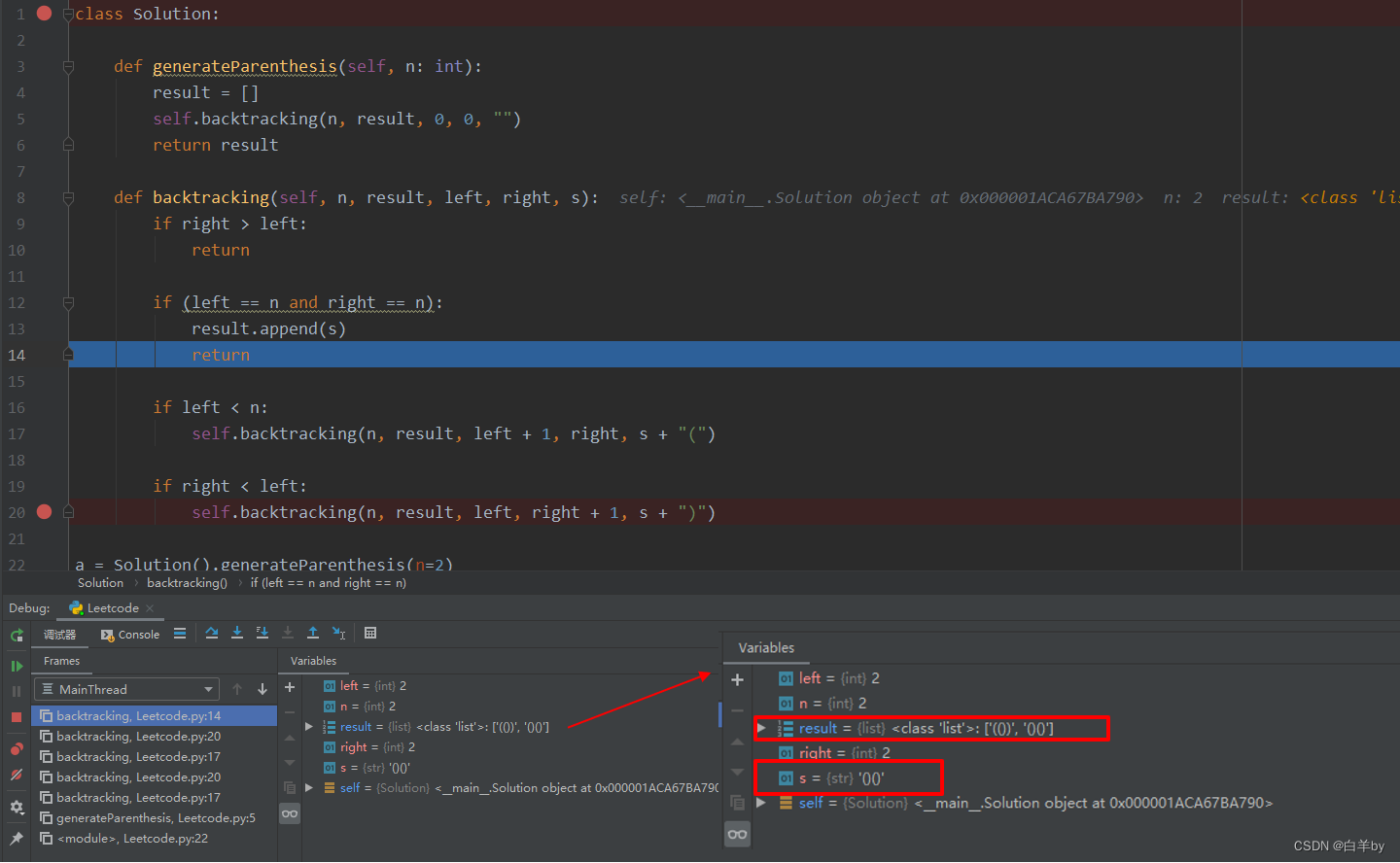
然后再回溯，代码结束执行

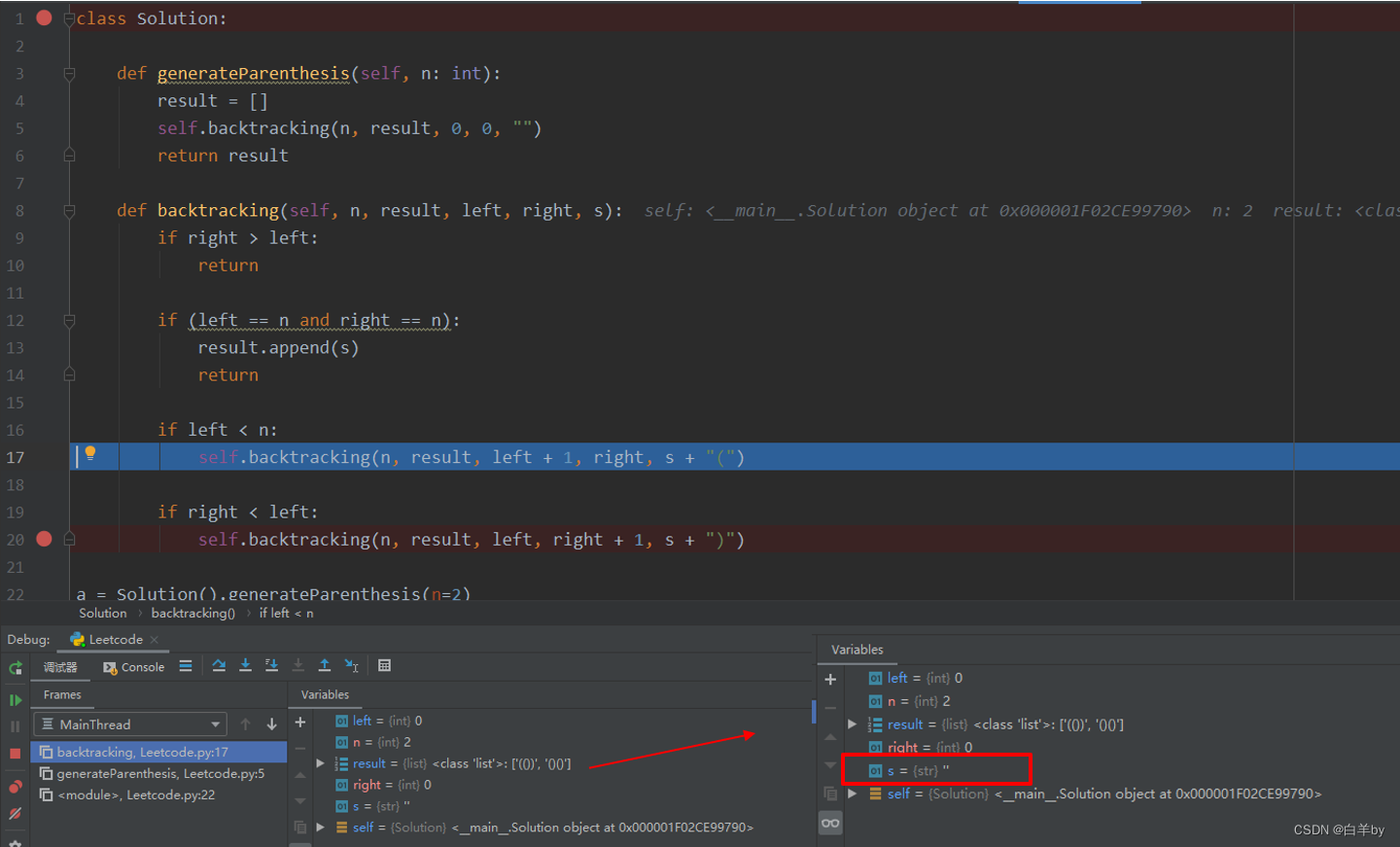
 所以大致的回溯流程如下

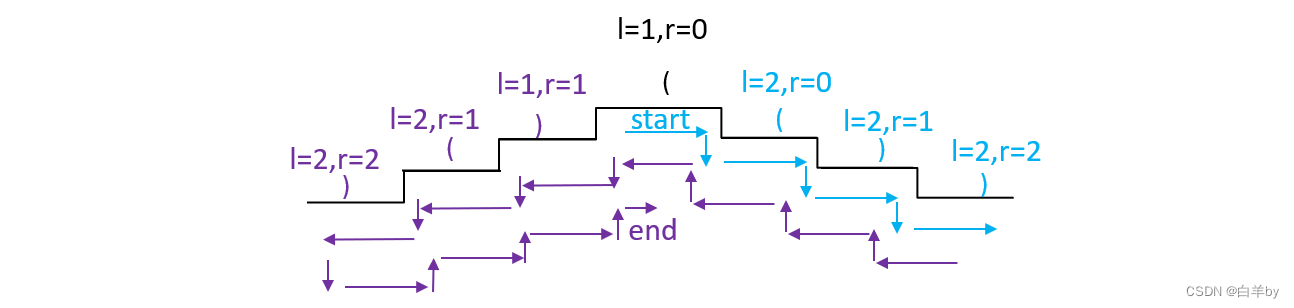
Java代码

class Solution {
    
    public List<String> generateParenthesis(int n) {
        List<String> result = new ArrayList<>();
        backtracking(n, result, 0, 0, "");
        return result;
    }
 
    private void backtracking(int n, List<String> result, int left, int right, String str) {
        if (right > left) {
            return;
        }
        if (left == n && right == n) {
            result.add(str);
            return;
        }
 
        if (left < n) {
            backtracking(n, result, left+1, right, str+"(");
        }
 
        if (right < left) {
            backtracking(n, result, left, right+1, str+")");
        }
    }
}