-
NDVI时间序列分析之Sen+MK分析全过程梳理
NDVI时间序列分析之Sen+MK分析全过程梳理
Sen斜率估计用于计算趋势值,通常与MK非参数检验结合使用,即先计算Sen趋势值,然后使用MK方法判断趋势显著性。
原理
Theil-Sen Median方法又被称为Sen斜率估计,是一种稳健的非参数统计的趋势计算方法。该方法计算效率高,对于测量误差和离群数据不敏感,常被用于长时间序列数据的趋势分析中。
β = m e d i a n ( x j − x i j − i ) , ∀ j > i \beta=median(\frac{x_j-x_i}{j-i}),∀j>i β=median(j−ixj−xi),∀j>i
式中: x j x_j xj 和 x i x_i xi 为时间序列数据。β大于0表示时间序列呈现上升趋势;β小于0表示时间序列呈现下降趋势。Mann-Kendall属于非参数检验方法,与其他参数检验的方法相比,不需要样本遵从一定的分布,受异常值干扰小,更适合顺序变量。Mann-Kendall检验已经在水文、气象趋势变化相关研究中得到了大量的成功应用,用于判断径流、降水、气候等的变化趋势的显著性。
R语言Sen+MK并行计算
R语言使用Terra包进行栅格并行计算,利用trend包sen.slope函数进行sen+mk的计算。对于下面代码的阅读,一定要看代码帮助!代码如下:
library(terra) library(trend) #输入一个文件夹内的单波段TIFF数据,在这里是历年的NDVI年最大值 flnames <- list.files(path = './ChinaYearMean/', pattern = '.tif$') fl <- paste0("./ChinaYearMean/", flnames) firs <- rast(fl) #Sen+MK计算 fun_sen <- function(x){ if(length(na.omit(x)) <34) return(c(NA, NA, NA)) #删除数据不连续含有NA的像元 MK_estimate <- trend::sens.slope(ts(na.omit(x), start = 1982, end = 2015, frequency = 1), conf.level = 0.95) #Sen斜率估计 slope <- MK_estimate$estimate MK_test <- MK_estimate$p.value Zs <- MK_estimate$statistic return(c(Zs, slope, MK_test)) } firs_sen = app(firs, fun_sen, cores=4 ) names(firs_sen) = c("Z", "slope", "p-value") #显示输出 plot(firs_sen) writeRaster(firs_sen, filename = "./firs_sen.tif", names=firs_sen@ptr[["names"]])- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
如果还没明白,下面二维码推荐一个培训班,有专门的R语言老师带着学习:
NDVI趋势制图
前面R语言计算完slope和Z值后,根据这两个结果就可以进行NDVI趋势制图了。
变化趋势划分
结合 S N D V I S_{NDVI} SNDVI和Z统计量划分NDVI变化趋势:
- slope
- -0.0005~0.0005稳定区域
- 大于或等于0.0005植被改善区域
- 小于-0.0005为植被退化区域
- Z统计量
- 置信水平0.05
- Z绝对值大于1.96显著
- Z绝对值小于等于1.96不显著
Slope划分
- Slope被划分为三级:
- S N D V I ≤ − 0.0005 S_{NDVI} \le -0.0005 SNDVI≤−0.0005 植被退化
- − 0.0005 ≥ S N D V I ≥ 0.0005 -0.0005 \ge S_{NDVI} \ge 0.0005 −0.0005≥SNDVI≥0.0005 植被生长稳定
- S N D V I ≥ 0.0005 S_{NDVI} \ge 0.0005 SNDVI≥0.0005 植被改善
- 使用重分类(Reclassify)对slope进行划分
- 由于slope.tif文件研究区范围外的值非空,所以在这里先裁剪了一下
- 裁剪所用矢量和栅格数据坐标系需要一致,否则范围容易出错
- 统一使用了WGS84地理坐标系作为空间参考
- 使用Model builder构建地理处理流
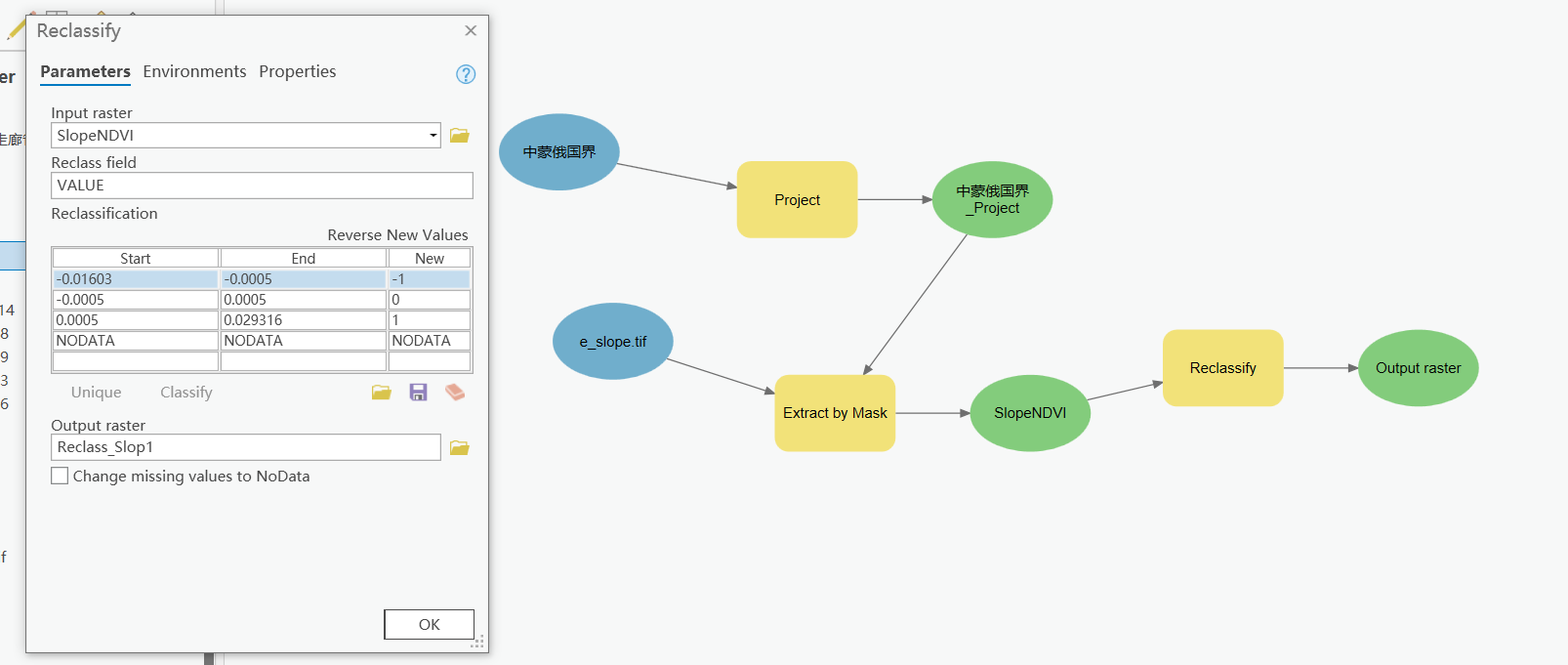
- 重分类结果:
- -1退化
- 0稳定
- 1改善
Z值划分
- 对Z值进行重分类,确定显著性
- ∣ Z s ∣ ≤ 1.96 \lvert Z_s\rvert \le 1.96 ∣Zs∣≤1.96 未通过95%置信度检验,不显著
- ∣ Z s ∣ ≥ 1.96 \lvert Z_s\rvert \ge 1.96 ∣Zs∣≥1.96 通过95%置信度检验,显著
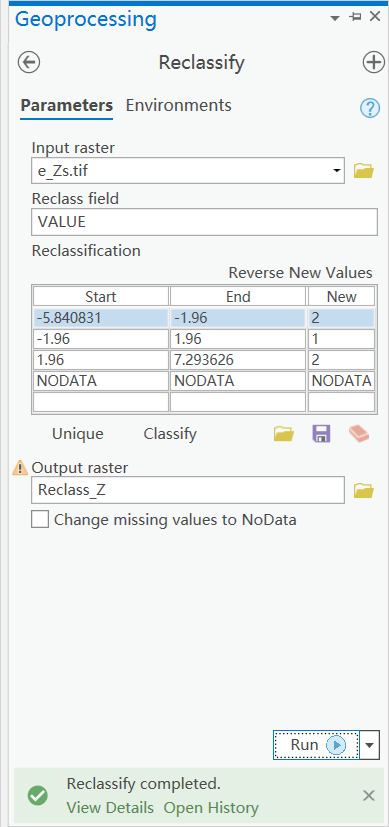
- 重分类结果:
- 1不显著
- 2显著
变化趋势计算
使用栅格计算器将Slope和Z值计算结果相乘,最后得到趋势变化划分
- -2严重退化
- -1轻微退化
- 0稳定不变
- 1轻微改善
- 2明显改善
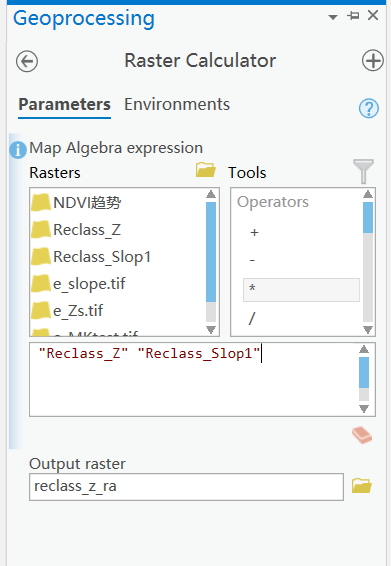
对计算完成后的栅格属性表里面不同种类的像元数进行统计,如此即可获得下面的NDVI变化趋势统计图表。
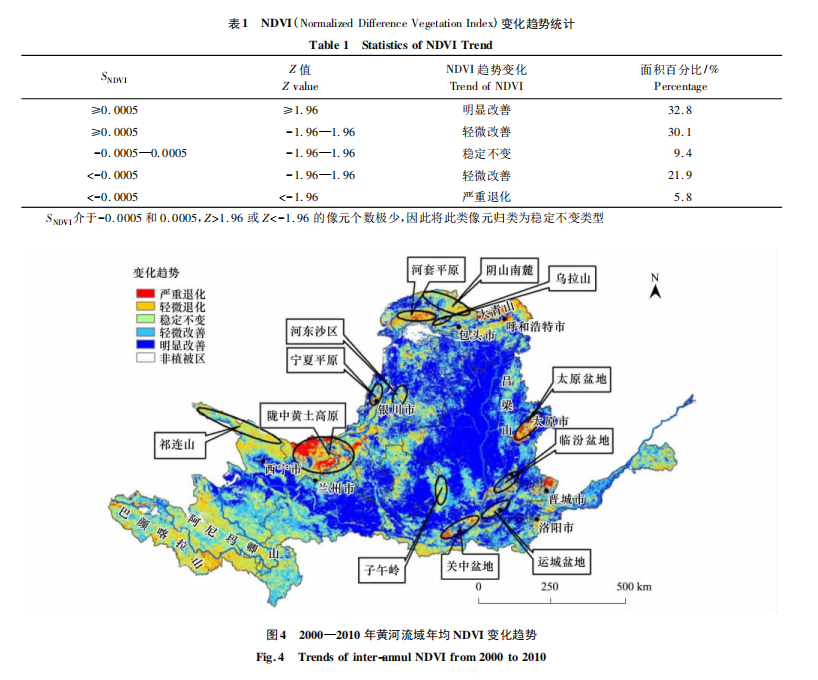
参考文献
- 袁丽华, 蒋卫国, 申文明, 等. 2000—2010年黄河流域植被覆盖的时空变化[J]. 生态学报, 2013, 33(24): 7798–7806.
- NDVI时间序列分析原理与实现(CV和Sen+MK趋势分析)
- 【文献阅读笔记】Sen+MK NDVI趋势分析的一些问题
- 基于Sen+MK的NDVI变化趋势统计分析
- 【文献阅读笔记】黄河流域植被变化时空分析
- https://www.rdocumentation.org/packages/trend/versions/1.1.1/topics/sens.slope

-
相关阅读:
点云从入门到精通技术详解100篇-基于尺度统一的三维激光点云与高清影像配准
【机器学习】贝叶斯分类器【上】
今天面试招了个18K的人,从腾讯出来的果然都有两把刷子···
Win10 + Ubuntu 双系统完美避坑删除 Ubuntu 教程
1. 快速体验 VSCode 和 CMake 创建 C/C++项目
北工大汇编——综合题(2)
上周热点回顾(4.18-4.24)
PHP框架开发实践 | 1024 程序员节:通过index.php找到对应的controller是如何实现的
React 如何导出excel
1、读写分离、分库分表
- 原文地址:https://blog.csdn.net/xydf_1992/article/details/125601533
