-
中国剩余定理(crt)和扩展中国剩余定理(excrt)
中国剩余定理(crt)
crt是用来对于一个一元线性同余方程求解的算法:

其中 m 1,m2,m3...mk为两两互质的整数
定理:我们设
,设
 设
设  =
=  为
为 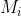 模
模  意义下的逆元.
意义下的逆元.这个一元线性同余方程组的通解为:

证明(来自百度百科):

下面上板子题:
【模板】中国剩余定理(CRT)/ 曹冲养猪 - 洛谷
https://www.luogu.com.cn/problem/P1495
- #include<bits/stdc++.h>
- #define int long long
- int a[20],b[20];
- void exgcd(int a,int b,int& x,int& y)
- {
- if(!b)
- {
- x=1,y=0;
- return;
- }
- exgcd(b,a%b,y,x);
- y-=a/b*x;
- }
- int inv(int a,int b)
- {
- int x,y;
- exgcd(a,b,x,y);
- return (x%b+b)%b;
- }
- int ksc(int a,int b,int p)
- {
- int res=0;
- while(b)
- {
- if(b&1)
- res=(res+a)%p;
- a=(a+a)%p;
- b>>=1;
- }
- return res;
- }
- void solve()
- {
- int n,M=1,ans=0;
- scanf("%lld",&n);
- for(int i=1;i<=n;i++)
- {
- scanf("%lld%lld",&a[i],&b[i]);
- M=M*a[i];
- }
- for(int i=1;i<=n;i++)
- {
- int m=M/a[i];
- int invm=inv(m,a[i]);
- ans=(ans+ksc(ksc(invm,M/a[i],M),b[i],M))%M;
- }
- printf("%lld\n",ans);
- return ;
- }
- signed main()
- {
- solve();
- return 0;
- }
扩展中国剩余定理(excrt)
拓展crt的作用也是求解下列方程组,但是约束条件不同:

其中 m 1,m2,m3...mk为不一定两两互质的整数.
我们每次选出两个方程利用exgcd进行合并即可,具体推算过程如下:

依照上面的证明两两结合,最后把全部结合即可.
证明完毕,来板子题耍耍:
【模板】扩展中国剩余定理(EXCRT) - 洛谷
 https://www.luogu.com.cn/problem/P4777
https://www.luogu.com.cn/problem/P4777- #include<bits/stdc++.h>
- #define int long long
- using namespace std;
- int exgcd(int a,int b,int &x,int &y)
- {
- if(!b)
- {
- x=1,y=0;
- return a;
- }
- int d=exgcd(b,a%b,y,x);
- y-=(a/b*x);
- return d;
- }
- int mul(int a,int b,int mod)
- {
- int res=0;
- while(b>0)
- {
- if(b&1) res=(res+a)%mod;
- a=(a+a)%mod;
- b>>=1;
- }
- return res;
- }
- void solve()
- {
- int n;
- scanf("%lld",&n);
- int a1,m1,a2,m2;
- scanf("%lld%lld",&m1,&a1);
- for(int i=2;i<=n;i++)
- {
- scanf("%lld%lld",&m2,&a2);
- int k1,k2;
- int d=exgcd(m1,m2,k1,k2);
- int c=((a2-a1)%m2+m2)%m2;
- if(c%d)
- {
- /*无解*/
- }
- k1=mul(k1,c/d,m2/d);
- a1=a1+k1*m1;
- m1=abs(m1/d*m2);
- }
- printf("%lld\n",(a1%m1+m1)%m1);
- return ;
- }
- signed main()
- {
- solve();
- return 0;
- }
-
相关阅读:
【大数据】CDC 技术:变化数据捕获
Java错题归纳day19
Camera2 学习总结
docker 安装 portainer
ROS2 从头开始:第3部分 — 创建自定义消息(.msg 和 .srv)和 Turtlebot3 服务节点的实践指南
【python】基础语法(三)--异常、模块、包
mysql---squid代理服务器
React插槽
92---Python 直角坐标系下绘制抛物线图像
KEIL5添加沁恒的ch55x芯片(其他非arm和stm32芯片也可使用类似的方法)
- 原文地址:https://blog.csdn.net/qq_49593247/article/details/125605331
