评估方法

• 在学习得到的模型投放使用之前，通常需要对其进行性能评估。为此，需使用一个“测试集”（testing set）来测试模型对新样本的泛化能力，然后以测试集上的“测试误差”（testing error）作为泛化误差的近似。
• 我们假设测试集是从样本真实分布中独立采样获得，所以测试集要和训练集中的样本尽量互斥。
• 给定一个已知的数据集，将数据集拆分成训练集S和测试集T，通常的做法包括留出法、交叉验证法、自助法。

留出法

• 直接将数据集划分为两个互斥集合，训练集S和测试集T
• 一般若干次随机划分，因为相同的数据集，相同的划分比例，也可以分成许多个不同的训练集和测试集，比如1000个数据集（其中包括500个正例，500个反例），按照7：3的比例进行划分就有$(C_{500}^{150}{)}^2$个不同分组。实际应用中，我们进行多次随机分组，所有实验取平均值，作为测试误差（泛化误差近似）。
• 训练/测试样本比例通常为2:1~4:1，即将大约2/3~4/5的样本用于训练，剩余样本作为测试。

交叉验证法

将数据集分层采样划分为k个大小相似的互斥子集，每次用k-1个子集的并集作为训练集，余下的子集作为测试集，最终返回k个测试结果的均值，k最常用的取值是10。

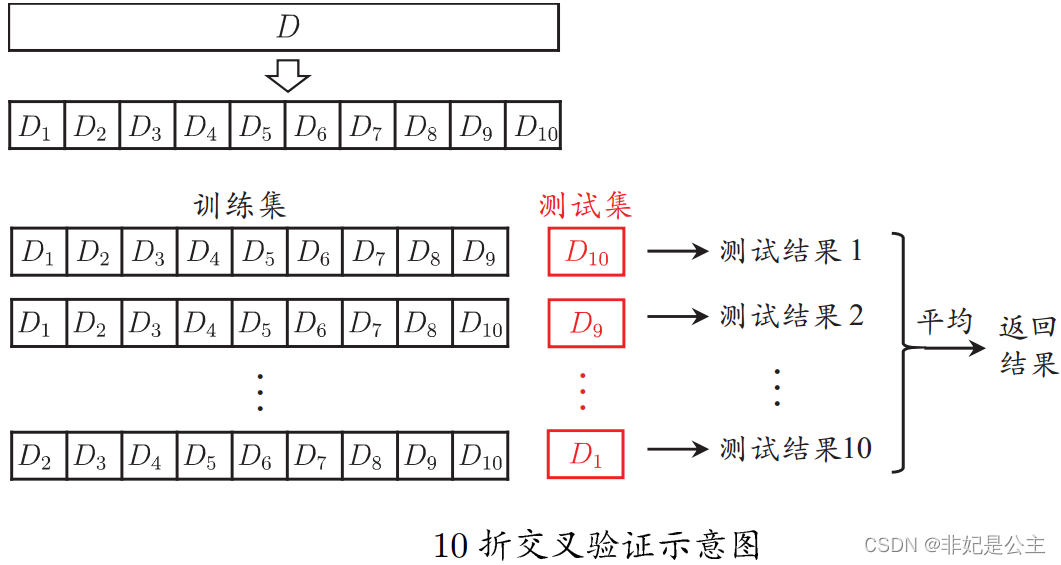
说明：D1，D2，D3……都是不同的子集，第一次测试$D_{10}$作为测试集，第二次测试$D_9$作为测试集……第10次测试$D_1$作为测试集，最终所有$测试结{果}_1$~$测试结{果}_{10}$取平均值作为测试误差。
与留出法类似，将数据集D划分为k个子集同样存在多种划分方式，为了减小因样本划分不同而引入的差别，k折交叉验证通常随机使用不同的划分重复p次，最终的评估结果是这p次k折交叉验证结果的均值，例如常见的“10次10折交叉验证”。

留一法

交叉验证法的极限情况，当每一个子集只有一个元素的时候，就是留一法，留一法有以下特点：

• 不受随机样本划分方式的影响
• 结果往往比较准确
• 当数据集比较大时，计算开销难以忍受

自助法

• 以自助采样法为基础，对数据集D有放回采样m次得到训练集 , 用做测试集实际模型与预期模型都使用m个训练样本（m约占样本总数量的$\frac{1}{3}$）

• 从初始数据集中产生多个不同的训练集，对集成学习有很大的好处

• 自助法在数据集较小、难以有效划分训练/测试集时很有用；由于改变了数据集分布可能引入估计偏差，在数据量足够时，留出法和交叉验证法更常用。

---

评估指标

要评估模型的好坏光有评估方法还不行，还得确定评估指标。

准确率与错误率

将模型结果与真实情况进行比较，最常用的两个指标是准确率和错误率
准确率：就是分对样本占测试样本总数的比例；
错误率：就是分错样本占测试样本总数的比例

查准率与查全率

真正：所有阳性中被分为正的比例
假正：所有阴性中被分为正的比例

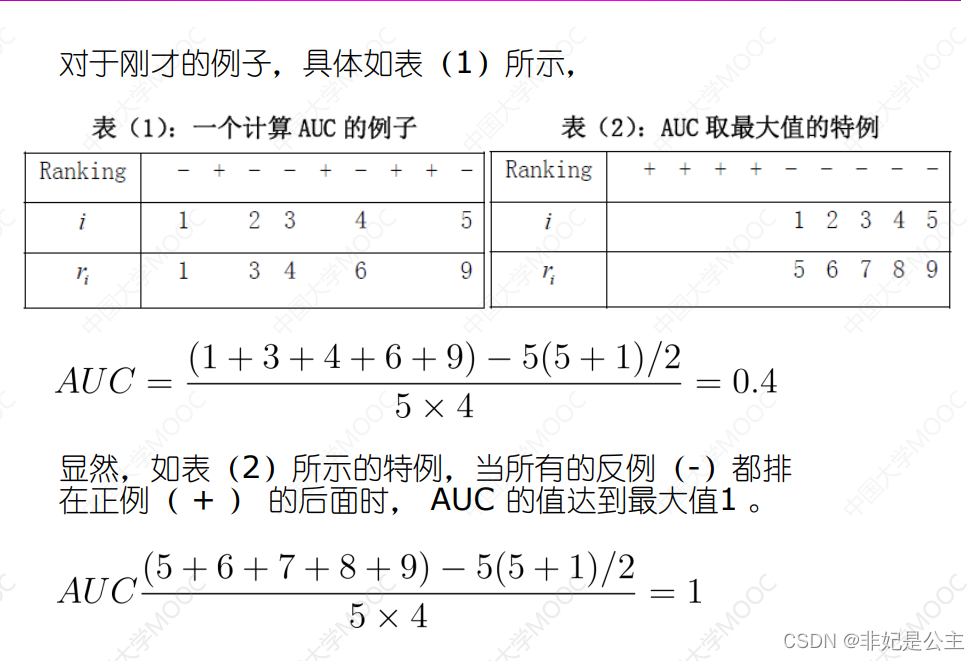
可以通过积分来计算面积的大小！

---

比较检验

关于性能比较有以下问题：

• 测试性能并不等于泛化性能
• 测试性能会随着测试集的变化而变化
• 很多机器学习算法本身有一定的随机性

所以，直接通过评估指标进行评价的做法是不可取的，因为我们获得的只是特定数据集上的表达效果，要想在数学上更加具有说服力，我们还需要进行假设检验。
假设检验为分类器的性能比较提供了重要依据，基于其结果我们可以推断出，若在测试集上观察到分类器A比B好，则A的泛化性能是否在统计意义上高于B，以及这个结论的把握有多大。

成对双边t检验

简单来说，分为以下步骤

1. 计算均值$\mu$
2. 计算方差${\sigma }^2$
3. 计算T统计量${\tau }_t$
4. 根据自由度$V$和置信度$\alpha$查表，得到临界值，如果${\tau }_t<临界值$，则说明“在置信度$\alpha$的前提下，可以认为两个分类器的性能没有显著差别，否则则认为两个分类器性能有显著差别，且平均错误率较小的分类器性能较优。”

Friedman检验与Nemenyi后续检验

成对双边t检验是在一个数据集上比较两个分类器的性能，而在很多时候，我们需要在一组数据集上比较多个分类器的性能，这就需要使用基于排序的Friedman 检验。
假定我们要在N个数据集上比较k个算法，首先使用留出法或者交叉验证法得到每个算法在每个数据集上的测试结果，然后在每个数据集上根据性能好坏排序，并赋序值1,2,…；若算法性能相同则平分序值，继而得到每个算法在所有数据集上的平均序值。

说明：上图在计算“卡方分布”${\tau }_{{\chi }^2}$
N：数据集的数量
k：模型数量
然后计算F统计量${\tau }_F$

说明：根据N和k查表，然后和F统计量${\tau }_F$比较，如果${\tau }_F<常用临界值$，则认为比较的算法是相同的，否则认为算法是显著不同的，只有当认为算法是显著不同的情况下，才进行下一步的$Nemenyi检验$。

说明：计算CD值，$q_{\alpha }$通过算法数量查表得到（k，N已知）

说明：比较算法之间的平均序值之差和CD的大小，如果大于CD认为显著不同，小于CD认为没有显著差别。

说明：Friedman检验图可以直观的表示各算法之间性能的差别，只是一种直观的表示形式，并没有新的方法。