-
论文笔记: 图神经网络 GAT
摘要: 分享对论文的理解. 原文见 Petar Velickovic, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, Yoshua Bengio, Graph attention networks, ICLR 2018, 1–12. 可以在 ArXiv: 1710.10903v3 下载. 完全难以估计影响力有多大!
1. 论文贡献
- 克服图卷积已有方法的缺点.
- 不需要耗时的矩阵运算 (如求逆).
- 不需要预知图的结构.
- 适用于归纳与演绎问题.
2. 基础思想
利用邻居的信息, 将图中节点原始属性映射到一个新的空间, 以支持后面的学习任务.
这个思想可能是不同图神经网络所共有的.3. 方案
Table 1. Notations. 符号 含义 备注 N N N 节点数 F F F 原始特征数 F ′ F' F′ 原始特征数 例中为 4 h \mathbf{h} h 结点特征集合 { h → 1 , … , h → N } \{\overrightarrow{h}_1,\dots, \overrightarrow{h}_N \} {h1,…,hN} h → i \overrightarrow{h}_i hi 第 i i i 个节点的特征 属于空间 R F \mathbb{R}^F RF h ′ \mathbf{h}' h′ 结点新的特征集合 { h → 1 ′ , … , h → N ′ } \{\overrightarrow{h}'_1,\dots, \overrightarrow{h}'_N \} {h1′,…,hN′} h → i ′ \overrightarrow{h}'_i hi′ 第 i i i 个节点的新特征 属于空间 R F ′ \mathbb{R}^{F'} RF′ W \mathbf{W} W 特征映射矩阵 属于 R F × F ′ \mathbb{R}^{F \times F'} RF×F′, 所有节点共享 N i \mathcal{N}_i Ni 节点 i i i 的邻居集合 包括 i i i 自己, 例中基数为 6 a → \overrightarrow{\mathbf{a}} a 特征权值向量 属于 R 2 F ′ \mathbb{R}^{2F'} R2F′, 所有节点共享, 对应于单层网络 α i j \alpha_{ij} αij 节点 j j j 对 i i i 的影响 所有邻居节点的影响之和为 1 α → i j \overrightarrow{\alpha}_{ij} αij 节点 j j j 对 i i i 的影响向量 长度为 K K K, 对应于多头 将节点特征映射到新空间, 利用注意力机制 a a a 计算节点间的关系
e i j = a ( W h → i , W h → j ) (1) e_{ij} = a(\mathbf{W}\overrightarrow{h}_i, \mathbf{W}\overrightarrow{h}_j) \tag{1} eij=a(Whi,Whj)(1)
这里仅当 j j j 是 i i i 在网络上的邻居时, 才计算 e i j e_{ij} eij.
将它进行 softmax, 使得节点 i i i 对应的权值和为 1.
α i j = s o f t m a x j ( e i j ) = exp ( e i j ) ∑ k ∈ N i exp ( e i k ) (2) \alpha_{ij} = \mathrm{softmax}_j(e_{ij}) = \frac{\exp(e_{ij})}{\sum_{k \in \mathcal{N}_i} \exp(e_{ik})}\tag{2} αij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)(2)
由于 a a a 将长度为 2 F ′ 2F' 2F′ 的列向量转换为一个标量, 可以将其写作一个相同长度的行向量 a → T \overrightarrow{\mathbf{a}}^{\mathrm{T}} aT. 再加上一个激活函数, 它就可以用单层的神经网络实现.α i j = exp ( L e a k y R e L u ( a → T [ W h → i ∥ W h → j ] ) ) ∑ k ∈ N i exp ( L e a k y R e L u ( a → T [ W h → i ∥ W h → k ] ) ) (2) \alpha_{ij} = \frac{\exp(\mathrm{LeakyReLu}(\overrightarrow{\mathbf{a}}^{\mathrm{T}}[\mathbf{W}\overrightarrow{h}_i \| \mathbf{W}\overrightarrow{h}_j]))}{\sum_{k \in \mathcal{N}_i} \exp(\mathrm{LeakyReLu}(\overrightarrow{\mathbf{a}}^{\mathrm{T}}[\mathbf{W}\overrightarrow{h}_i \| \mathbf{W}\overrightarrow{h}_k]))}\tag{2} αij=∑k∈Niexp(LeakyReLu(aT[Whi∥Whk]))exp(LeakyReLu(aT[Whi∥Whj]))(2)
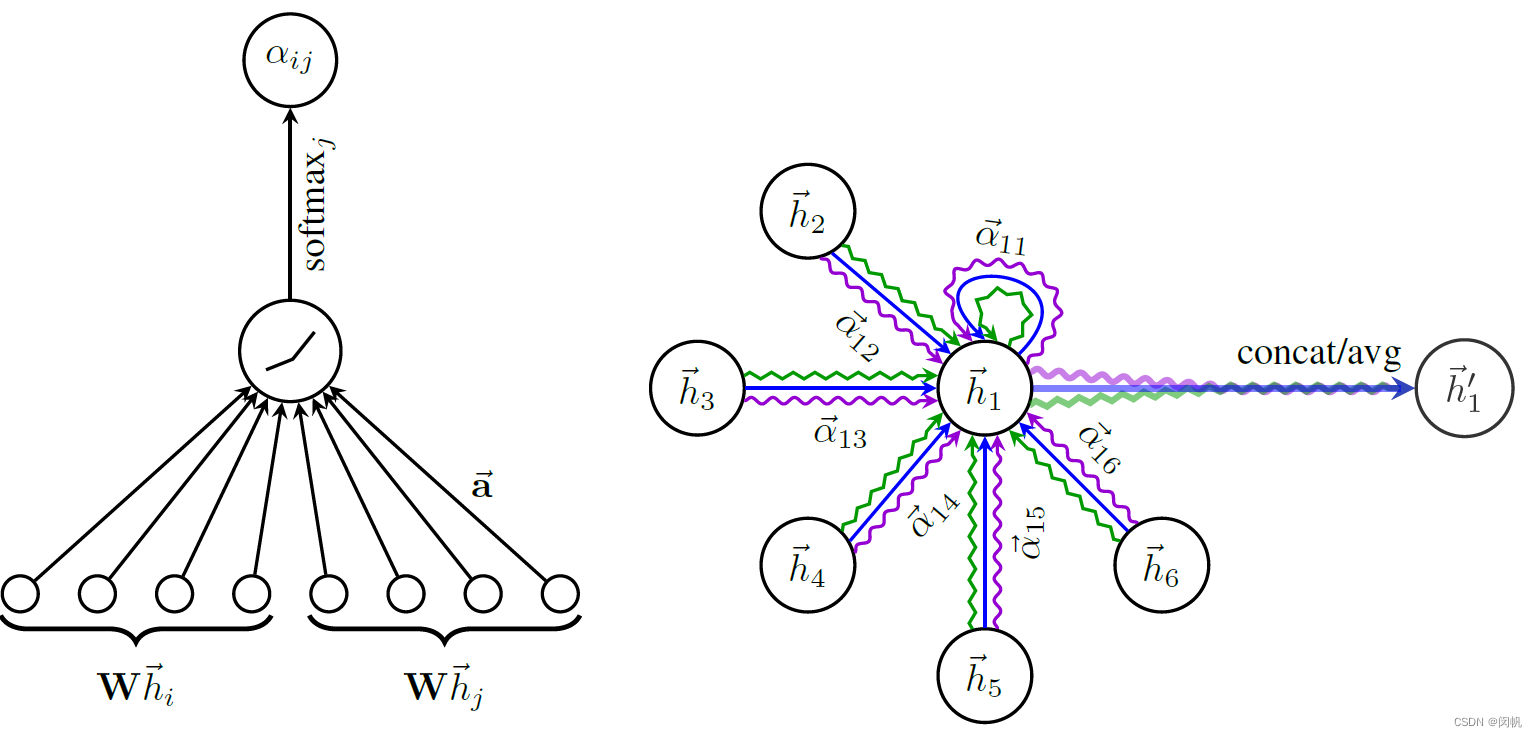
图 1. GAT 核心方案. 左: F ′ = 4 F' = 4 F′=4 的时候, 从 W \mathbf{W} W 映射到的新空间为 4 维. 相应的 2 F ′ = 8 2F' = 8 2F′=8 维. 向量 a → \overrightarrow{\mathbf{a}} a 由所有的节点共享. 右: K = 3 K = 3 K=3 个头.3.1 方案一: 单头
h → i ′ = σ ( ∑ j ∈ i α i j W h → j ) (4) \overrightarrow{h}'_i = \sigma\left(\sum_{j \in \mathcal{i}} \alpha_{ij} \mathbf{W} \overrightarrow{h}_j\right)\tag{4} hi′=σ(j∈i∑αijWhj)(4)
所有邻居节点先映射到新空间 (如 4 维), 然后根据其影响力加权求和, 并用 sigmoid 等非线性激活函数, 最终获得的还是 4 维向量.3.2 方案二: 多头连接
h → i ′ = ∥ k = 1 K σ ( ∑ j ∈ N i α i j k W k h → j ) (5) \overrightarrow{h}'_i = \|_{k = 1}^K \sigma\left(\sum_{j \in \mathcal{N}_i} \alpha^k_{ij} \mathbf{W}^k \overrightarrow{h}_j\right)\tag{5} hi′=∥k=1Kσ⎝⎛j∈Ni∑αijkWkhj⎠⎞(5)
K K K 个头分别获得相应的新向量, 图 1 右展示了 3 个头, 因此最后的向量为 3 × 4 = 12 3 \times 4 = 12 3×4=12 维.3.3 方案三: 多头平均
h → i ′ = σ ( 1 K ∑ k = 1 K ∑ j ∈ N i α i j k W k h → j ) (5) \overrightarrow{h}'_i = \sigma \left(\frac{1}{K} \sum_{k = 1}^K \sum_{j \in \mathcal{N}_i} \alpha^k_{ij} \mathbf{W}^k \overrightarrow{h}_j\right)\tag{5} hi′=σ⎝⎛K1k=1∑Kj∈Ni∑αijkWkhj⎠⎞(5)
仅仅是平均值, 最后的向量为 4 4 4 维.4. 疑问
- 问题: 这里的
W
\mathbf{W}
W 与
a
→
\overrightarrow{\mathbf{a}}
a 如何学习?
猜测: 可以从相关工作, 即图神经网络里面获得必要的知识. 这篇论文只是想描述不一样的核心技术.
如果将这个网络的输出作为其它网络的输入 (最终输出为类标签等), 有可能就可以进行相应学习. - 问题: 为什么计算影响力的时候使用 LeakyReLU, 而计算最终特征向量的时候使用 sigmoid?
强行解释: 前者只是与后者区别开 (非必要), 后者是改变线性 (有必要).
5. 小结
- 利用 W \mathbf{W} W 线性映射到新空间.
- 利用 a → \overrightarrow{\mathbf{a}} a 计算各邻居的影响力 α i j \alpha_{ij} αij. a → \overrightarrow{\mathbf{a}} a 仅针对相应属性, 而不受邻居编号影响. α i j \alpha_{ij} αij 的计算涉及 LeakyReLU 激活函数的使用.
- 利用多头增加稳定性.
- 求均值、使用非线性函数激活都不会改变向量的维度.
-
相关阅读:
什么是学习能力?如何提高学习能力?
Java数组—精讲篇
如何制作一篇公众号推文?纯干货
在服务器的docker里 装anacond3深度学习环境的全流程超基础
HybrIK流程
k8s中无法获取到nginx-ingress的客户端真实ip地址x-forwarded-for
JavaEE进阶 - Spring MVC 程序开发 - 细节狂魔
2024年阿里云服务器新用户购买一个月多少钱?
【毕业设计】37-基于单片机智能楼宇消防监控系统设计(原理图工程+仿真工程+源代码+答辩论文+答辩PPT)
【TypeScript】什么是字面量类型、类型推断、类型拓宽和类型缩小?
- 原文地址:https://blog.csdn.net/minfanphd/article/details/125596788