MATLB|电动车智能充电模式及电力高峰需求预测

目录

0 写在前面

1 电动车

1.1 电动车（EV）

1.2 电动汽车充电

1.3 智能充电和车联网（V2G）

1.4 V2G 应用

 1.5 可再生能源可用性

1.6 基于价格的收费

2 电动车智能充电

2.1 智能充电

2.2 实时电价

2.3 智能充电模式——算例1

2.4 洞见

2.5 智能充电模式——算例2

2.6 报摊问题——算例3

 2.7 需求量与概率——算例4

3 完整Matlab代码实现

---

 

0 写在前面

电力系统强大的CVX学习（Matlab&Python）

1 电动车

1.1 电动车（EV）

I 降低维护成本

I 降低税收

I 更便宜的燃料（电）

I 政府补贴

                  

1.2 电动汽车充电

I典型电池容量：30kWh−100kWh

I车载充电器：1.9–22 kW

I直流非车载充电器：50–350 kW

I充电级别

        I级别1:0–10 kW

        I级别2:10–50 kW

        I级别3:50–350 kW 23/64

对电力系统的影响:

           

1.3 智能充电和车联网（V2G）

I 使用电动汽车电池通过双向 EV 充电器将电力回馈到电网

I 优势：可再生能源的存储、减少高峰需求、辅助服务等

I 挑战：优化控制、双向充电器、电池退化、标准化、监管框架、 ETC

1.4 V2G 应用

I 本地负载平衡

I 根据负载调整充电时间/功率

I 优先平衡多个充电点

I 可再生能源利用

I 基于价格的充电/放电

I 调峰

I 电网备份 

 1.5 可再生能源可用性

           

1.6 基于价格的收费

   

2 电动车智能充电

2.1 智能充电

I 你有一辆 EV，可以在家充电。

I 电价是实时电价（RTP）。

I 你需要 20kW 来为你的电动汽车充电。

I 充电器的额定功率为 2kW。

假设电动汽车可以在一天中的任何时间充电。我现在，你需要确定什么时间充电，以尽量减少一天的电费

2.2 实时电价

              

2.3 智能充电模式——算例1

                     

其中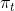是价格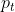，是充电功率。

 运行结果：

                 

2.4 洞见

智能充电？

我是不是太激进了？

电池退化成本如何？

我到家、离开和开车的时间怎么样？

我的充电状态？

我有多辆车？

我的方便和隐私？

电力系统可靠性？

面对这些问题，我们进入下一个算例，约束条件那些充分考虑。

2.5 智能充电模式——算例2

           

还差一个约束：

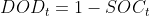
 机器学习：数据拟合:

                   

        

损失函数定义为:

              

电力高峰需求预测:

            

2.6 报摊问题——算例3

I一家公司生产冬装。

I 公司必须在知道确切需求 d 之前，在冬季前 3 个月承诺具体的生产数量 x。

I 在看到需求 d 后，公司决定以正常价格 πr 出售的数量 yr，以及以残值/折扣价 πs 出售的数量 ys。

I 这称为不确定性下的决策，因为决策 x 是在不确定性需求 d 下做出的。

 两阶段随机规划

I决策变量：生产量x

I观望决策：常规价格量yr，折扣价格量ys

I目标：最小化生产成本和预期未来成本

            ​​​​​​​

组合两个阶段：

    

假设需求 d 是具有 S 个场景 (d1,...,ds) 的离散随机变量，每个场景 di 具有概率 pi。

相应地，每个情景 di 的销售量有和。 

 

举例：

(1)假设有3个场景，d1 = 10，概率为1/4； d2 = 30，概率为 5/12； d3 = 50，概率为 1/3.

(2)生产外套的单位成本：c = 5，正常价格：πr = 10，折扣价：πs = 3。

(3) 生产能力：

   

结果：

 

 2.7 需求量与概率——算例4

优化问题实际上是如何解决的？

(1)无约束问题

设置导数（一维）或梯度（高维）

   

那么如何求∇xf(x) = 0

I 直接解决方案：分析计算

        梯度下降:

        牛顿法:

  

(2)约束优化

障碍法：通过无约束优化的近似问题:

当 t → 0 时，这接近原始问题:

最大化拉格朗日对偶问题

(3)举例

I 如果很难定义场景怎么办？如果我们的分布不是离散的怎么办？

I 在大多数一般条件下采样就足够了.

 

 

3 完整Matlab代码实现

本文只展现部分代码，全部代码见：🍞正在为您运送作品详情