669. 修剪二叉搜索树 ●●

给你二叉搜索树的根节点 root ，同时给定最小边界 low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

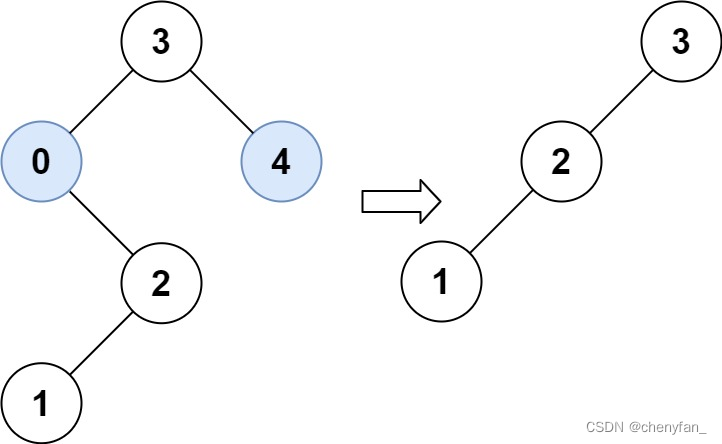
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

对于二叉搜索树，
如果 root->val < low，那么修剪后的二叉树一定出现在根节点的右边；
如果 root->val > high，那么修剪后的二叉树一定出现在根节点的左边。

递归

时间复杂度：O(N)，其中 N 是给定的树的全部节点。我们最多访问每个节点一次。
空间复杂度：O(N)，即使我们没有明确使用任何额外的内存，在最糟糕的情况下，我们递归调用的栈可能与节点数一样大。

• 从上往下遍历，在对某一节点进行修剪操作后，还需要重新再判断一次该节点（返回修剪后的子树）；

class Solution {
public:
    TreeNode* pre = nullptr;
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root == nullptr) return nullptr;
        if(root->val < low){
            return trimBST(root->right, low, high);	// 返回修剪后的右子树
        }else if(root->val > high){
            return trimBST(root->left, low, high);	// 返回修剪后的左子树
        }
        root->left = trimBST(root->left, low, high);	// 修剪左子树
        root->right = trimBST(root->right, low, high);	// 修剪右子树
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

• 从下往上遍历，修剪子树不影响上面节点的结构，同时不需要重新判断某一节点也能遍历完成整棵树。

class Solution {
public:
    TreeNode* pre = nullptr;
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root == nullptr) return nullptr;
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        if(root->val < low){		
            // root->left = nullptr;	// 删除左子树
            return root->right;		// 并用右子树替换该节点
        }else if(root->val > high){
            // root->right = nullptr;	// 删除右子树
            return root->left;		// 并用左子树替换该节点
        }
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

迭代

由于搜索树的有序性，因此不需要用栈来模拟递归过程，处理过程为：

1. 先将根节点 root 移动到区间范围内，确定新的根节点；
2. 处理当前根节点左子树中不符合条件的节点；
3. 处理当前根节点右子树中不符合条件的节点。

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root == nullptr) return nullptr;
        // 确定在区间内的根节点
        while(root != nullptr){         
            if(root->val < low){
                root = root->right;
            }else if(root->val > high){
                root = root->left;
            }else{
                break;
            }
        }
        // 此时root已经在[low, high] 范围内，处理左孩子元素小于low的情况
        TreeNode* curr = root;
        while(curr != nullptr){
        	// 【注意此处为while循环，直到找到符合条件 > low 的左子节点进行替换】
            while(curr->left != nullptr && curr->left->val < low){		
                curr->left = curr->left->right;
            }
            curr = curr->left;
        }
        // 此时root已经在[low, high] 范围内，处理右孩子大于high的情况
        curr = root;
        while(curr != nullptr){
        	// 【注意此处为while循环】
            while(curr->right != nullptr && curr->right->val > high){	
                curr->right = curr->right->left; 
            }
            curr = curr->right;
        }

        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36