异构图

相比同构图，异构图里可以有不同类型的节点和边。这些不同类型的节点和边具有独立的ID空间和特征。 例如在下图中，”用户”和”游戏”节点的ID都是从0开始的，而且两种节点具有不同的特征。

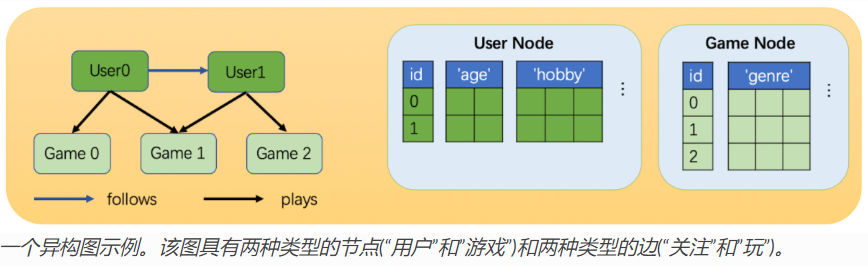
因此异构图才是最能够表达和适用我们真实世界的各种表达的。

下面可以使用DGL创建一个如下的异构图：

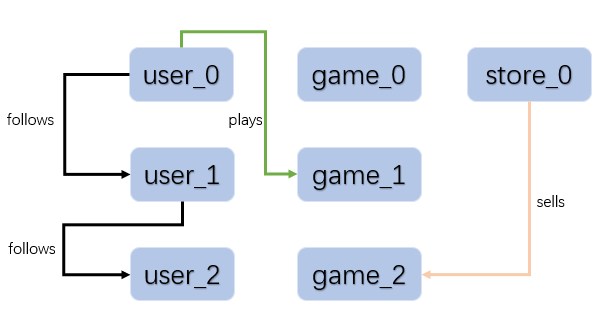
一共有三种实体，三种关系的异构图

import dgl
g = dgl.heterograph({
    ('user', 'follows', 'user') : ([0, 1], [1, 2]),
    ('user', 'plays', 'game') : ([0], [1]),
    ('store', 'sells', 'game')  :([0], [2])})
print(g)
1
2
3
4
5
6

输出结果：

Graph(num_nodes={'game': 3, 'store': 1, 'user': 3},
      num_edges={('store', 'sells', 'game'): 1, ('user', 'follows', 'user'): 2, ('user', 'plays', 'game'): 1},
      metagraph=[('store', 'game', 'sells'), ('user', 'user', 'follows'), ('user', 'game', 'plays')])
1
2
3

DGL中创建异构图有许多方式，上面介绍的是通过类似三元组的方式创建
例如(‘store’, ‘sells’, ‘game’)，是指store指向game的sells关系，([0], [2])则是指store_0到game_2的单向sells关系，因此消息传递的时候也只能从game_2传到sells更新。

虽然game_0没有在图中用到，但是他会默认创建。

从上面的异构图输出可以看出一共有7个节点，3种关系，符合预期。

下面是关于异构图的一些操作

print(g.etypes)  # 获取边的类型
print(g.ntypes) # 获取节点的类型
print(g.number_of_nodes('user')) # 获取user节点的个数
print(g.metagraph().edges()) # 获取二元组
print(g.nodes('user')) # 查看user节点编号
g.nodes['user'].data['HP'] = th.ones(3, 1) # 设置/获取"user"类型的节点的"HP"特征
print(g.nodes['user'].data['HP'][0]) # 获取"user"0类型的节点的"HP"特征
g.edges['sells'].data['money'] = th.zeros(1, 2) # 设置/获取"sells"类型的边的"money"特征
print(g.edges['sells'].data['money'][0]) # 获取"sells"类型边0的"money"特征
hg = dgl.to_homogeneous(g) # 将异构图转换成同构图
print(hg.ndata[dgl.NTYPE]) # 原始节点类型
print(hg.ndata[dgl.NID]) # 原始的特定类型节点ID
print(hg.edata[dgl.ETYPE]) # 原始边类型
print(hg.edata[dgl.EID]) # 原始的特定类型边ID
1
2
3
4
5
6
7
8
9
10
11
12
13
14

HeteroGraphConv

异形图卷积在它们的关联关系图上应用子模块，从源节点读取特征并将更新的特征写入目标节点。如果多个关系具有相同的目标节点类型，则它们的结果将通过指定的方法聚合。如果关系图没有边，则不会调用相应的模块。

因为对于异构图卷积，存在不同类型的边，那么每种类型的边需要各自设置参数，不能像同构图那样共享参数。

初始化

import dgl.nn.pytorch as dglnn
dglnn.HeteroGraphConv(mods, aggregate='sum')
1
2

需要传入两个参数，第一个mods是字典类型，内容为{关系名：模型层, }
第二个是聚合函数，默认sum，因为一共节点可能会有多个边汇聚信息过来，聚合信息更新节点信息需要聚合函数发挥作用。

forward

forward(g, inputs, mod_args=None, mod_kwargs=None)
1

forward有四个参数可以输入，mod_args和mod_kwargs默认即可
g代表输入的图数据
inputs也是字典类型，代表输入的节点的特征

例子

就用上面的异构图来进行异构图卷积操作

首先创建异构图：

import dgl
g = dgl.heterograph({
    ('user', 'follows', 'user') : ([0, 1], [1, 2]),
    ('user', 'plays', 'game') : ([0], [1]),
    ('store', 'sells', 'game')  :([0], [2])})
print(g)
1
2
3
4
5
6

然后初始化异构图卷积层

# 三种关系都设置为输入2维节点特征输出3维特征
import dgl.nn.pytorch as dglnn
conv = dglnn.HeteroGraphConv({
    'follows' : dglnn.GraphConv(2, 3),
    'plays' : dglnn.GraphConv(2, 3),
    'sells' : dglnn.GraphConv(2, 3)},
    aggregate='sum')
1
2
3
4
5
6
7

然后传入参数得出结果：

import torch as th
h1 = {'user' : th.ones((g.number_of_nodes('user'), 2)),
      'game' : th.ones((g.number_of_nodes('game'), 2)),
      'store' : th.ones((g.number_of_nodes('store'), 2))}
print(h1)
h2 = conv(g, h1)
print(h2)
print(h2.keys())
1
2
3
4
5
6
7
8

输出结果：

{'user': tensor([[1., 1.],
        [1., 1.],
        [1., 1.]]), 'game': tensor([[1., 1.],
        [1., 1.],
        [1., 1.]]), 'store': tensor([[1., 1.]])}
{'game': tensor([[ 0.0000,  0.0000,  0.0000],
        [ 0.6098, -1.0385,  0.2647],
        [ 0.1339,  0.6426, -0.6454]], grad_fn=<SumBackward1>), 'user': tensor([[ 0.0000,  0.0000,  0.0000],
        [ 1.0880,  0.2894, -0.8723],
        [ 1.0880,  0.2894, -0.8723]], grad_fn=<SumBackward1>)}
dict_keys(['game', 'user'])
1
2
3
4
5
6
7
8
9
10
11

结果中只有game和user因为这两种类型的节点涉及到更新的操作，store由于没有边指向他，不需要进行更新因此也不需要输出节点的新特征。

参考

https://docs.dgl.ai/guide_cn/graph-heterogeneous.html#guide-cn-graph-heterogeneous
https://docs.dgl.ai/generated/dgl.nn.pytorch.HeteroGraphConv.html#dgl.nn.pytorch.HeteroGraphConv