目录

欧拉函数

欧拉定理

拓展欧拉定理(欧拉降幂)

---

欧拉函数

在数论中，有正整数n，欧拉函数是小于n的正整数中与n互质的数的数目.

它的通式如下:

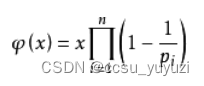
 φ(n)=n*(1-1/p1)*(1-1/p2)*(1-1/p3)*(1-1/p4)*……*(1-1/pn)

这里的p是数字n的质因数.

故此可以得到欧拉函数的求法:

int eular(int n)
{
    int ans = n;
    for(int i=2; i*i <= n; ++i)
    {
        if(n%i == 0)
        {
            ans = ans/i*(i-1);
            while(n%i == 0)
                n/=i;
        }
    }
    if(n > 1) ans = ans/n*(n-1);
    return ans;
}

以上是打表求法.

欧拉函数的性质(phi即为欧拉函数):

1.当m,n互质时,phi(m*n)=phi(m)*phi(n);

2.i%p==0时,phi(i*p)=p*phi(i);

3.小于N且与N互质的所有数之和为phi(N)*N/2;

4.N为质数时,phi(N)=N-1

5.phi(1)=1;

根据以上的欧拉函数的性质,我们可以将它们和欧拉筛相结合:

void get_eular()
{
    phi[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(vis[i]==0)
        {
            p[++cnt]=i;
            phi[i]=i-1;
        }
        for(int j=1;j<=cnt&&i*p[j]<=n;j++)
        {
            vis[i*p[j]]=1;
            if(i%p[j]==0)
            {
                phi[p[j]*i]=p[j]*phi[i];
                break;
            } 
            phi[p[j]*i]=(p[j]-1)*phi[i];
        }
    }
}

欧拉定理

欧拉定理其实也属于欧拉函数的一个性质(证明我以后有空再补上吧qwq,贴个百度百科的图):

定义

对任意两个正整数 a, n，如果两者互质，那么 aφ(n)≡1(mod n)。

证明

 费马小定理

若存在整数a,p，a为整数，p为质数，那么a(p-1)≡ 1(mod p)。

费马小定理是欧拉定理的一种特殊情况（当n为质数时φ(n)为n-1）

应用

逆元的定义：
对于a*b≡1(mod p)，b是a在模m下a的逆元。（只有a与p互质时存在逆元）
应用
当p为质数时由费马小定理a^(p-1)≡ 1(mod p)得，逆元b为a^(p-2);
当p不是质数时则需使用欧拉定理，提前求出p的欧拉函数，逆元b为a^(φ(n)-1)。

拓展欧拉定理(欧拉降幂)

在求解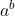mod p时,在指数b大到我们不能用快速幂和暴力去求解时,可以考虑用欧拉降幂求解.欧拉降幂的式子是(证明先缓缓):

洛谷模板

【模板】扩展欧拉定理 - 洛谷https://www.luogu.com.cn/problem/P5091

#include<bits/stdc++.h>
#define int long long
using namespace std;
int eular(int x)
{
    int ans=x;
    for(int i=2;i*i<=x;i++)
    {
        if(x%i==0)
        {
            ans=ans/i*(i-1);
            while(x%i==0)
                x/=i;
        }
    }
    if(x>1)
        ans=ans/x*(x-1);
    return ans;
}
int ksm(int x,int y,int m)
{
    int res=1;
    while(y)
    {
        if(y%2==1)
            res=res*x%m;
        y>>=1;
        x=x*x%m;
    }
    return res;
}
void solve()
{
    int a,m,eularm,numb=0;
    string b;
    cin>>a>>m>>b;
    eularm=eular(m);
    for(int i=0;i<b.size();i++)
    {
        numb=numb*10+(b[i]-'0');
        if(numb>eularm)
        {
            numb%=eularm;
            numb+=eularm;
        }       
    }
    if(numb>=eularm)
        numb+=eularm;
    cout<<ksm(a,numb,m);
}
signed main()
{
    solve();
    return 0;
}