Leetcode（81）——搜索旋转排序数组 II

题目

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（$0<=k<nums.length$）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

你必须尽可能减少整个操作步骤。

示例 1：

输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true

示例 2：

输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

提示：

$1$ <= nums.length <= $5000$
$-10^4$ <= nums[i] <= $10^4$
题目数据保证 $nums$ 在预先未知的某个下标上进行了旋转
$-10^4$ <= target <= $10^4$

进阶：

• 这是 搜索旋转排序数组 的延伸题目，本题中的 $nums$ 可能包含重复元素。
• 这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

题解

方法一：二分查找

思路

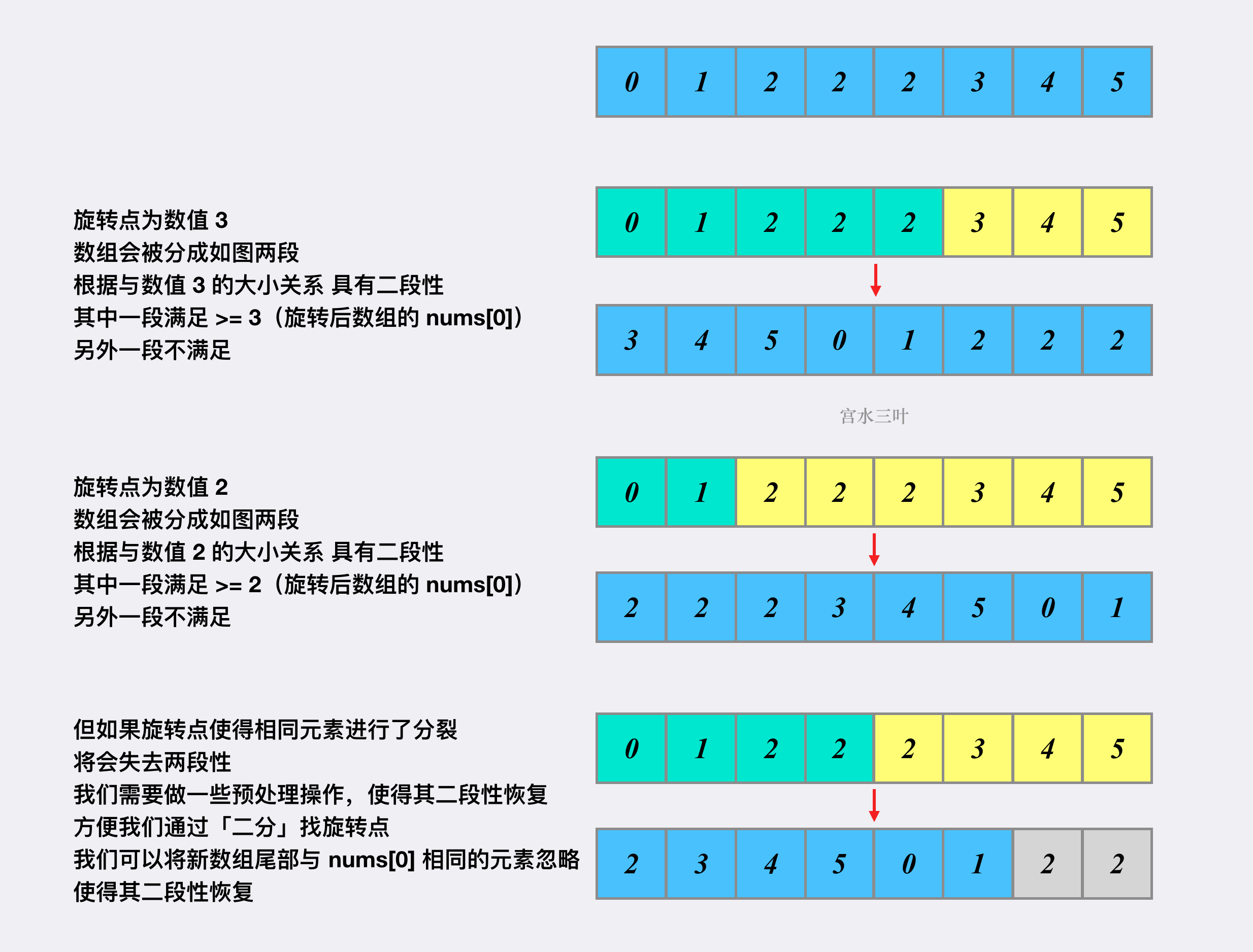
​​  但和 33. 搜索旋转排序数组 不同的是，本题元素并不唯一。这意味着我们无法直接根据与 nums[0]nums[0] 的大小关系，将数组划分为两段，即无法通过「二分」来找到旋转点。因为「二分」的本质是二段性，并非单调性。只要一段满足某个性质，另外一段不满足某个性质，就可以用「二分」。

​​  即使数组被旋转过，我们仍然可以利用这个数组的递增性，使用二分查找。对于当前的中点，如果它指向的值小于等于右端，那么说明右区间是排好序的；反之，那么说明左区间是排好序的。如果目标值位于排好序的区间内，我们可以对这个区间继续二分查找；反之，我们对于另一半区间继续二分查找。
​​  注意，因为数组存在重复数字，如果中点和左端的数字相同，我们并不能确定是左区间全部相同，还是右区间完全相同。在这种情况下，我们可以简单地将左端点右移一位，然后继续进行二分查找。

​​  例如 $\text{nums}=[3,1,2,3,3,3,3]$，$\text{target}=2$，首次二分时无法判断区间 $[0,3]$ 和区间 $[4,6]$ 哪个是有序的。

代码实现

Leetcode 官方题解：

class Solution {
public:
    bool search(vector<int> &nums, int target) {
        int n = nums.size();
        if (n == 0) return false;
        else if (n == 1) return nums[0] == target;
        int l = 0, r = n - 1, mid;
        while (l <= r) {
            mid = (l + r) / 2;
            if (nums[mid] == target) return true;
            if (nums[l] == nums[mid] && nums[mid] == nums[r]) {
            	// 去掉首尾重复的元素，保证二段性
                ++l;
                --r;
            } else if (nums[l] <= nums[mid]) {	// 左区间是排好序的了
                if (nums[l] <= target && target < nums[mid]) 	// 判断 target 是否在左区间里
                    r = mid - 1;
                else l = mid + 1;
            } else {	// 右区间是排好序的了
                if (nums[mid] < target && target <= nums[n - 1])	// 判断 target 是否在右区间里
                    l = mid + 1;
                else r = mid - 1;
            }
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

复杂度分析

时间复杂度：$O(\log n)$。最坏情况下数组元素均相等且不为 $\text{target}$，我们需要访问所有位置才能得出结果。此时的时间复杂度为 $O(n)$，其中 $n$ 是数组 $\text{nums}$ 的长度。
空间复杂度：$O(1)$