能带你起飞的【数据结构】成王第十一篇:堆

前言

 

二叉树的顺序存储

之前写的二叉树都是以链式存储的,左孩子,右孩子存地址,每个节点通过left和right串联起来.

今天写顺序存储一棵二叉树 

存储方式 

使用数组保存二叉树结构，方式即将二叉树用层序遍历方式放入数组中。

一般只适合表示完全二叉树，因为非完全二叉树会有空间的浪费。

这种方式的主要用法就是堆的表示。

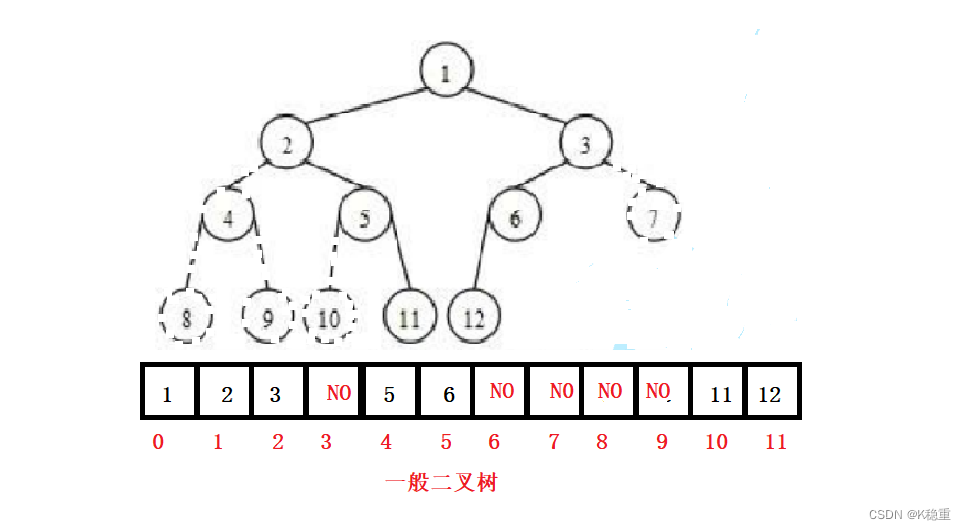 下标关系 :

已知双亲(parent)的下标，则：

左孩子(left)下标 = 2 * parent + 1;

右孩子(right)下标 = 2 * parent + 2;

已知孩子（不区分左右）(child)下标，则： 双亲(parent)下标 = (child - 1) / 2;

堆(heap) 

1. 堆逻辑上是一棵完全二叉树

2. 堆物理上是保存在数组中

3. 满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆

4. 反之，则是小堆，或者小根堆，或者最小堆

5.堆的基本作用是，快速找集合中的最值

实现一个堆 

堆分为大根堆和小根堆

我们首先要把这棵二叉树调整为大根堆

要变成大根堆,每棵子树也必须是大根堆

首先比较左右孩子,左右孩子大的再和根节点比较大小,孩子比根大就互换,小就不变.

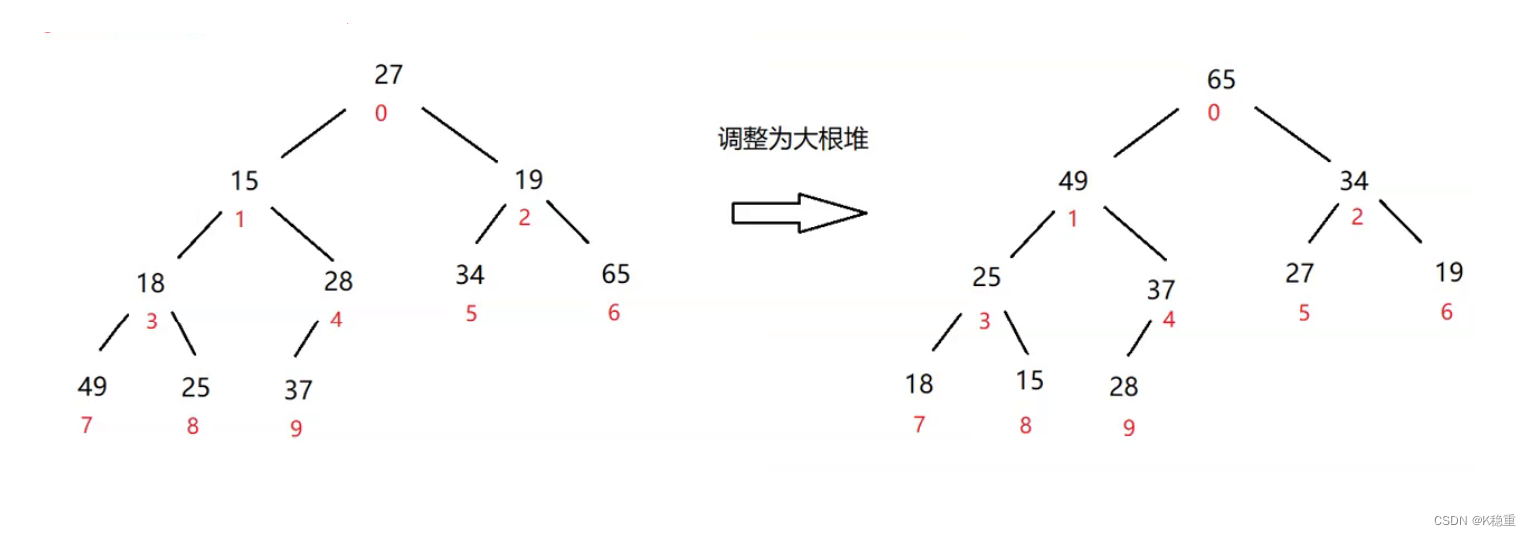
 只要变成大根堆一定能保证最上面的根节点是最大的元素

大根堆不是说就是有序的

总结:

1.调整是从最后一棵子树出发的

2.每棵子树的调整都是向下调整的(根和左右孩子去比较,根小根就下来了,这就叫做向下调整)

问题:

1.如何找到最后一棵子树?

整棵树是一个数组,那么最后一个元素就是len - 1

得到父亲节点parent = ((len-1)-1)/2

2.parent--就可以遍历完每棵子树

3.写一个向下调整的函数

4.每棵树的调整结束位置,如何判定?

每棵树调整的结束位置实际上都是一样的len

public class TestHeap {
    public int elem[];
    public int usedSize;
 
    public TestHeap(){
        this.elem = new int[10];
    }
 
    /**
     * 向下调整函数的实现
     * @param parent 每棵树的根节点
     * @param len 每棵树的调整的结束位置
     */
    public void shiftDown(int parent ,int len){
        int child = 2 * parent + 1;
        //1.最起码是有左孩子的,至少是有一个孩子的
        while(child < len){
            if(child + 1 < len && elem[child] > elem[child + 1]){
                child++;//保证当前左右孩子最大值的下标
            }
            if(elem[child] > elem[parent]){
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                parent = child;
                child = 2 * parent + 1;
 
                
            }else{
                break;
            }
 
        }
 
    }
   
    //创建一个大根堆
    public void createBigHeap(int[] array ){
        for (int i = 0; i < array.length ; i++) {
            //将数据放到 elem 当中
            elem[i] = array[i];
            usedSize++;
        }
        //parent到 < 0 的时候就不能进行向下调整了
        for (int parent = (usedSize - 1 -1)/2; parent >= 0 ; parent--) {
            //调整
            shiftDown(parent,usedSize);
        }
 
    }
}

 此时我们就有了一个堆

大堆还是小堆需要验证:

 打印结果

 小堆 

入队操作(向上调整):

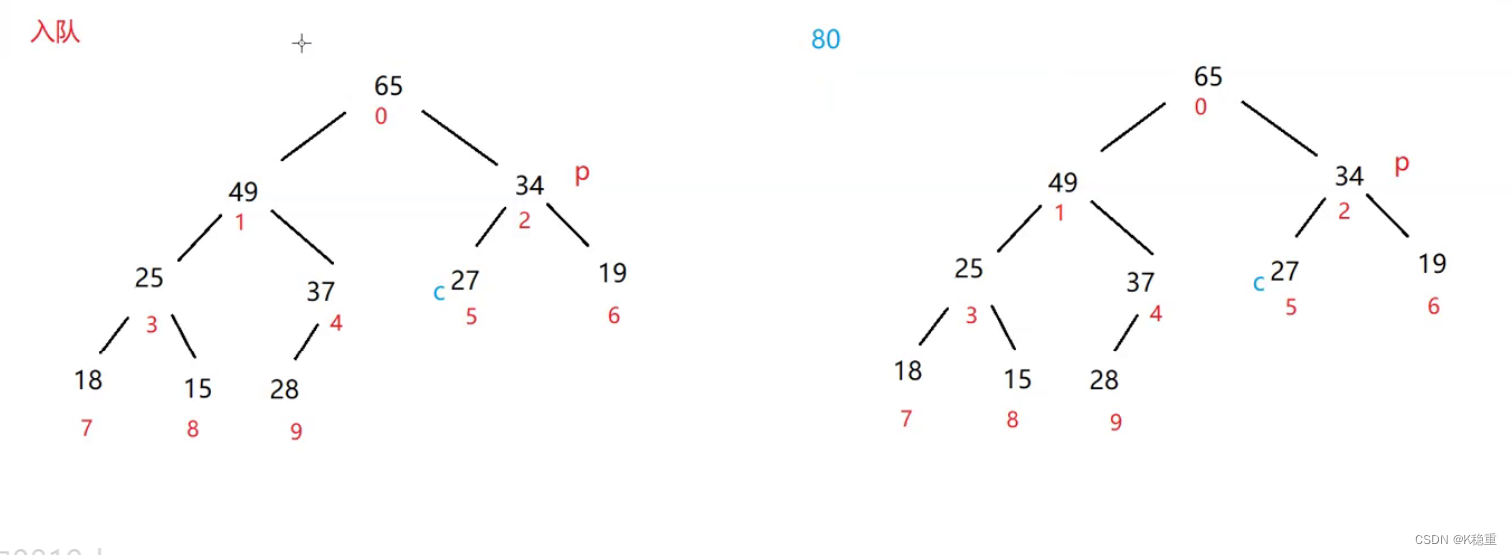 假设在没满的情况下,要放一个80到里面,如何放

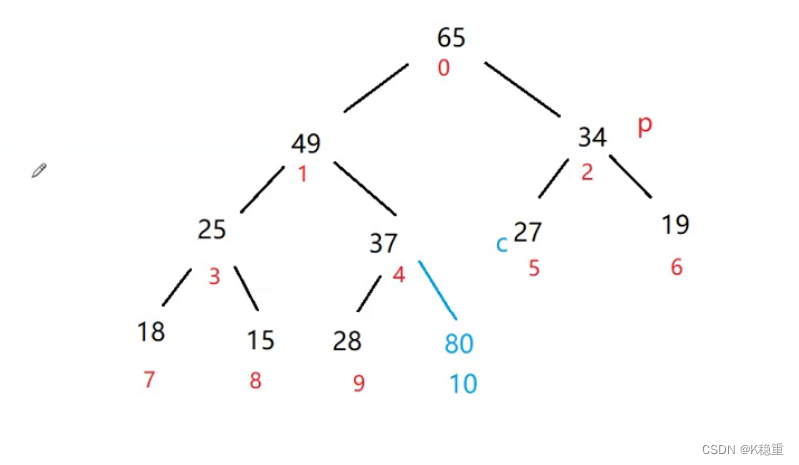 把80放到最后一个,此时80的下标就是10 

那么此时是大根堆吗?不是,需要进行调整

直接让80跟37比较(因为在插入80之前已经是大根堆了)

交换

这就是向上调整

出队列(向下调整):

每次出队列都得保证出最大的或者最小的 

第一步:交换0下标和最后一个元素

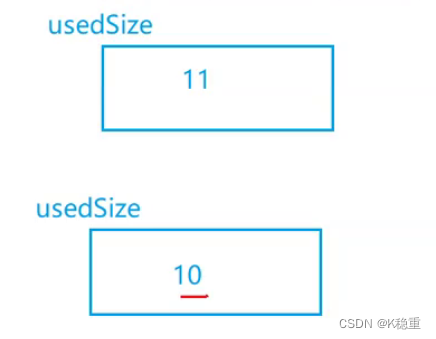
每次出都相当于usedSize都会减减 

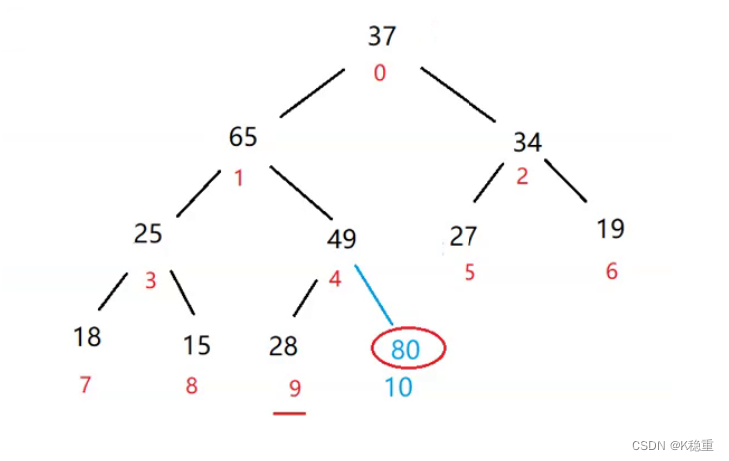
此时80就出出去了 

此时我们就可以发现只有一棵树不是大根堆(0下标这棵树)

第二步:调整0下标这棵树就可以了(进行向下调整)

完整代码

public class TestHeap {
    public int elem[];
    public int usedSize;
 
    public TestHeap(){
        this.elem = new int[10];
    }
 
    /**
     * 向下调整函数的实现
     * @param parent 每棵树的根节点
     * @param len 每棵树的调整的结束位置
     */
    public void shiftDown(int parent ,int len){
        int child = 2 * parent + 1;
        //1.最起码是有左孩子的,至少是有一个孩子的
        while(child < len){
            if(child + 1 < len && elem[child] > elem[child + 1]){
                child++;//保证当前左右孩子最大值的下标
            }
            if(elem[child] > elem[parent]){
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                parent = child;
                child = 2 * parent + 1;
 
                
            }else{
                break;
            }
 
        }
 
    }
   
    //创建一个大根堆
    public void createBigHeap(int[] array ){
        for (int i = 0; i < array.length ; i++) {
            //将数据放到 elem 当中
            elem[i] = array[i];
            usedSize++;
        }
        //parent到 < 0 的时候就不能进行向下调整了
        for (int parent = (usedSize - 1 -1)/2; parent >= 0 ; parent--) {
            //调整
            shiftDown(parent,usedSize);
        }
 
    }
    //向上调整
    private void shiftup(int child){
        int parent = (child - 1)/2;
        while(child > 0){
            if(elem[child] > elem[parent]){
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child - 1)/2;
            }
        }
 
    }
     //堆建好了往里面放元素
    public void offer( int val){
        if(isFull()){
            //扩容
            elem = Arrays.copyOf(elem,2*elem.length);
        }
        elem[usedSize++] = val;
        shiftup(usedSize-1);
 
    }
    //判满不满
    public boolean isFull(){
 
        return usedSize == elem.length;
    }
      //出队列
    public int poll(){
        if(isEmpty()){
          throw new RuntimeException("优先级队列为空");
        }
        int tmp = elem[0];
        elem[0] = elem[usedSize - 1];
        elem[usedSize - 1] = tmp;
        shiftDown(0,usedSize);
        return tmp;
    }
    public boolean isEmpty(){
        return usedSize == 0;
    }
}