一、最短路径快速算法（SPFA）

最短路径快速算法（SPFA）是Bellman–Ford算法的改进，该算法在加权有向图中计算单源最短路径。该算法被认为可以很好地处理随机稀疏图，尤其适用于包含负权重边的图。
SPFA算法的功劳归于段范丁。
SPFA的基本思想与Bellman–Ford算法相同，因为每个顶点都被用作松弛其相邻顶点的候选顶点。与后者相比的改进是，SPFA没有盲目尝试所有顶点，而是维护一个候选顶点队列，并仅在该顶点松弛时向队列中添加一个顶点。此过程将重复，直到不再松弛顶点。
最短路径快速算法
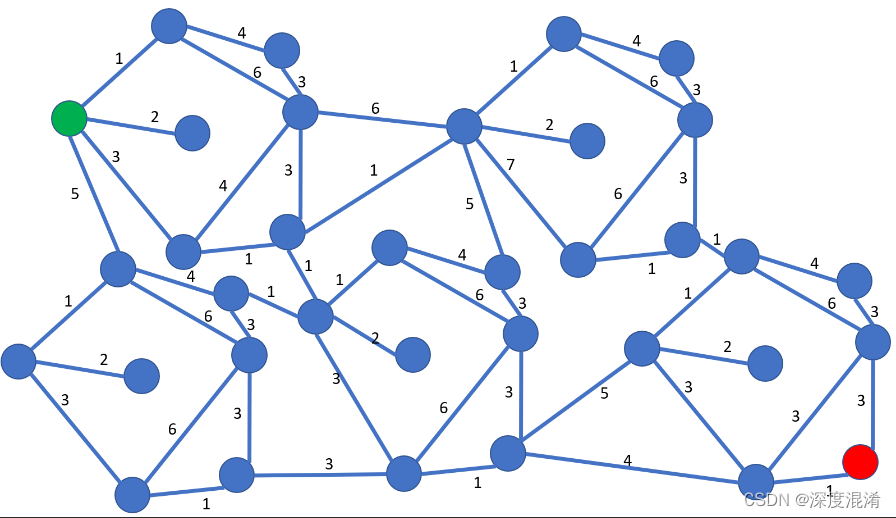
视觉：红线是覆盖的最短路径（迄今为止观察到）。蓝线表示松弛发生的位置，即将v与Q中的节点u连接，这使得从源到v的路径更短。
SPFA的最坏情况复杂性与Bellman–Ford的相同，因此对于具有非负边权的图，Dijkstra算法是首选。
对于某些数据，SPFA算法可能很慢。
假设您想要从顶点1到顶点n的最短路径，那么我们可以添加边（i，i+1），其中随机权重为1<=i<n（因此最短路径应为1-2-…-n），并随机添加4n条其他重边。在这种情况下，与其他最短路径算法相比，SPFA算法将非常慢。
 

给定一个具有V顶点、E边和源顶点S的有向加权图。任务是找到从源顶点到给定图中所有其他顶点的最短路径。

方法：最短路径快速算法基于Bellman-Ford算法，其中每个顶点用于松弛其相邻顶点，但在SPF算法中，保留一个顶点队列，并且仅当该顶点松弛时，才将顶点添加到队列中。此过程将重复，直到不再松弛顶点。
可以执行以下步骤来计算结果：
创建一个数组d[]，以存储所有顶点到源顶点的最短距离。以无穷大初始化此数组，但d[S]=0（其中S是源顶点）除外。
创建队列Q并在其中推送起始源顶点。
当队列不为空时，对图中的每条边（u、v）执行以下操作
如果d【v】>d【u】+边缘重量（u，v）d【v】=d【u】+边缘重量（u，v）
如果顶点v不在队列中，则将顶点v推入队列。
注：术语松弛意味着更新连接到顶点v的所有顶点的成本，如果这些成本可以通过包括通过顶点v的路径来提高。这可以通过最短路径的估计和螺旋拉伸弹簧的长度之间的类比来更好地理解，螺旋拉伸弹簧不是为压缩而设计的。起初，最短路径的成本被高估了，就像一个伸展的弹簧。随着路径变短，估计成本降低，弹簧放松。最终，找到最短路径（如果存在），弹簧已松弛至其静止长度。
 

 

最短路径算法是为解决最短路径问题而设计的一系列算法。最短路径问题是大多数人直觉上熟悉的问题：给定两点A和B，它们之间的最短路径是什么？然而，在计算机科学中，最短路径问题可以有不同的形式，因此需要不同的算法来解决它们。

为了简单和通用性，最短路径算法通常对一些输入图GG进行操作。该图由一组顶点VV和连接它们的边EE组成。如果边具有权重，则该图称为加权图。有时这些边是双向的，图形称为无向的。有时图形中甚至可能有循环。对于特定的图类型，每一个细微的差异都使一个算法比另一个算法工作得更好。下图显示了一个图表示例。
还有不同类型的最短路径算法。可能需要找到点A和B之间的最短路径，但可能需要找到点A和图中所有其他点之间的最短路径。
最短路径算法有很多应用。如前所述，Google或Apple maps等地图软件使用最短路径算法。它们对于道路网、运营和物流研究也很重要。最短路径算法对于计算机网络（如Internet）也非常重要。

任何帮助您选择路线的软件都使用某种形式的最短路径算法。例如，谷歌地图为您设置了起点和终点，并将为您解决最短路径问题。
 

二、图算法集锦

1、Bellman-Ford算法

Bellman-Ford算法解决了一般情况下的单源问题，其中边可以具有负权重，并且图是有向的。如果图形是无向的，则必须通过在每个方向上包含两条边来进行修改，以使其具有方向性。

Bellman Ford的特性是，它可以检测到从源可以到达的负权重循环，这意味着不存在最短路径。如果存在负权重循环，则路径可以在该循环上无限运行，从而将路径成本降低到-\infty−∞.

如果没有负权重循环，Bellman Ford将返回最短路径的权重以及路径本身。

2、Dijkstra算法

Dijkstra的算法利用广度优先搜索（不是单源最短路径算法）来解决单源问题。它确实在图形上放置了一个约束：不能有负权重边。然而，对于这一约束，Dijkstra大大改进了Bellman Ford的运行时。

Dijkstra算法有时也用于解决所有对最短路径问题，只需在VV中的所有顶点上运行它即可。同样，这要求所有边权重都为正。

3、拓扑排序

对于有向无环图（DAG），出现了一个非常有用的工具来寻找最短路径。通过对图中的顶点进行拓扑排序，最短路径问题可以在线性时间内求解。

拓扑排序是对所有顶点进行排序，以便对于EE中的每条边（u，v）（u，v），uu在排序中位于vv之前。在DAG中，最短路径总是定义得很好，因为即使有负权重边，也不可能有负权重循环。

4、Floyd-Warshall算法

Floyd-Warshall算法解决了所有对的最短路径问题。它使用动态规划方法来实现这一点。Floyd Warshall可能存在负边缘重量。

Floyd Warshall利用了以下观察结果：从A到C的最短路径要么是从A到B的最短路径加上从B到C的最短路径，要么是已经找到的从A到C的最短路径。这看似微不足道，但正是因为如此，Floyd Warshall才能够以经典的动态编程方式从较小的最短路径构建最短路径。

5、约翰逊算法

Floyd Warshall适用于稠密图（表示多条边），Johnson的算法适用于稀疏图（表示少条边）。在稀疏图中，Johnson算法的渐近运行时间低于Floyd Warshall算法。

Johnson的算法利用了重新加权的概念，并在多个顶点上使用Dijkstra的算法，以在完成边缘重新加权后找到最短路径。

参考：

C#，图（Graph）的数据结构设计与源代码https://blog.csdn.net/beijinghorn/article/details/125133711?spm=1001.2014.3001.5501

SPFA源代码：

using System;
using System.Collections;
using System.Collections.Generic;
 
namespace Legalsoft.Truffer.Algorithm
{
	public partial class Graph
	{
		public int[] Shortest_Path_Faster_Algorithm(int S, int V)
		{
			int[] d = new int[V + 1];
 
			bool[] inQueue = new bool[V + 1];
 
			for (int i = 0; i <= V; i++)
			{
				d[i] = int.MaxValue;
			}
			d[S] = 0;
 
			Queue<int> q = new Queue<int>();
			q.Enqueue(S);
			inQueue[S] = true;
 
			while (q.Count != 0)
			{
				int u = q.Peek();
				q.Dequeue();
				inQueue[u] = false;
				List<Edge> list = FindEdgesFrom(u);
				for (int i = 0; i < list.Count; i++)
				{
					int v = list[i].Second;
					int weight = list[i].Weight;
 
					if (d[v] > d[u] + weight)
					{
						d[v] = d[u] + weight;
 
						if (!inQueue[v])
						{
							q.Enqueue(v);
							inQueue[v] = true;
						}
					}
				}
			}
 
			return d;
		}
	}
 
	public static partial class GraphDrives
	{
		public static string SPFA()
		{
			int V = 5;
			int S = 1;
			Graph g = new Graph(V);
			g.AddEdge(1, 2, 1);
			g.AddEdge(2, 3, 7);
			g.AddEdge(2, 4, -2);
			g.AddEdge(1, 3, 8);
			g.AddEdge(1, 4, 9);
			g.AddEdge(3, 4, 3);
			g.AddEdge(2, 5, 3);
			g.AddEdge(4, 5, -3);
 
			int[] d = g.Shortest_Path_Faster_Algorithm(S, V);
 
			return String.Join(",", d);
		}
	}
}