简介

本文参考：https://blog.csdn.net/sanqima/article/details/48831679
网上关于这个算法没有提供做题的思路，我结合我自己的一些思考写一下我的思路。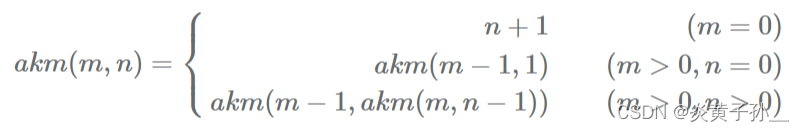

从上到下分别标记为1式、2式、3式，这个在代码注解里会用到
下面的函数名为《数据结构教程》(北航的)的页数和题号

递归算法

这个很简单没啥好讲的

//Ackerman递归算法
int P121_3_1(int m, int n)
{
	if (m == 0) {
		return n + 1;
	}
	if (m != 0 && n == 0) {
		return P121_3_1(m - 1, 1);
	}
	return P121_3_1(m - 1, P121_3_1(m, n - 1));
}
1
2
3
4
5
6
7
8
9
10
11

非递归算法

误区

我先讲一下误区：
递归转堆栈的时候，我最开始认为一定要把每一层的操作信息都给记录下来，然后再操作堆栈。例如下面这道题：

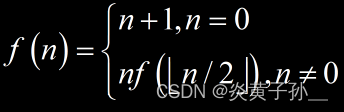
// n=0,f(n)=n+1
// n!=0,f(n)=nf(向下取整(n/2))
int P121_2(int n)
{
	int stack[M] = { 0 }, top = -1, ret = 0;
	stack[++top] = n;
	// 现将所有操作放入堆栈中
	while (n != 0) {
		n = n / 2;
		stack[++top] = n;
	}
	ret = 1;
	// 最后再统一操作堆栈
	while (top != 0) {
		ret = stack[--top] * ret;
	}
	return ret;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

这个思路在面对上面这种简单题的时候，是没问题的。但是面对Ackerman函数不行。
原因：
放入堆栈的时候，如果是式1和式2，都可以直接得到下一个子函数的自变量，但是碰见式3就麻烦了。
例如
ACK(0,3),可用式1，直接得结果。
ACK(3,0)，可用式2，ACK(3,0) = ACK(2,1) , 这样我们可以把 (3,0) 和 (2,1) 两组数分别入栈。
但是ACK(2,2) ，可用式3，ACK(2,2) = ACK(1,ACK(2,1)) 就只能先入栈 (2,1) 而无法直接入栈等式右侧的(1, ACK(2,1))

示例

策略：我们只管眼前的，把眼前的先处理好，如果碰见式3 ，先入栈子函数，不管式3的整体式子。为了编程上的方便，每层需要有4个变量

//[0]: m
//[1]: n
//[2]: 如果完成了计算,则是本层的f(m,n);
//  如果没完成计算，则代表本层是怎么得到.2: 代表2式得到,  3:代表3式得到
//[3]: 是否完成了本层计算,1为完成,0为没有完成
int st[M][4]
1
2
3
4
5
6

所以，这意味着，不能把每一层的操作信息都给记录下来，然后再操作堆栈。而是要一边入栈，一边又要操作堆栈。当遇到 式3 的时候，例如 ACK(1, ACK(2,1)) ，先别管外层，先入栈里面的 (2,1)
以ACK(2,2) 为例，PUSH代表入栈，POP代表出栈，PEEK代表查看而不修改栈顶指针
PUSH([2,2,3,0]) , ACK(2,2) = ACK(1,ACK(2,1)) , 3式
PUSH([2,1,3,0]) , ACK(2,1) = ACK(1 , ACK(2,0)), 3式
PUSH([2,0,2,0]) , ACK(2,0) = ACK(1,1) , 2式
PUSH([1,1,3,0]) , ACK(1,1) = ACK(0,ACK(1,0)) , 3式
PUSH([1,0,2,0]) , ACK(1,0) = ACK(0,1) ,2式
PUSH([0,1]) , ACK(0,1) = 2
至此，碰到了第一个 1 式的结果，开始进行 POP出栈操作

---

POP([0,1]) , 当前结果 = 2
POP([1,0,2,0]) , 式2, 当前结果= ACK(0,1) = 2
PEEK([1,1,3,0]) , 式3, 当前结果 = ACK(0 , ACK(1,0)) = ACK(0, 2)
遇见 式3 再次进行 PUSH 操作，并且要把 [1,1,3,0] 改成 [1,1,4,0]，这代表 式3 已经完成过子函数的计算了。
PUSH([0,2]) , ACK(0,2) = 3, 1式
至此，又碰到 1 式了，开始进行pop操作

---

POP([0,2]) , 当前结果为 3
POP([1,1,4,0]) ，当前结果为 ACK(1,1) = ACK(0,2) = 3
POP([2,0,2,0]) , 式2, 当前结果为 ACK(2,0) = ACK(1,1) = 3
…

按照这种操作方式，遇到式3，把子函数推入堆栈中先处理，然后处理完后继续处理式3的整体。

代码示例

#define M 5000 
// 这里堆栈大小要大一下，ACK(m,n)的 m 和 n 要在4以内，否则堆栈可能会溢出。
// 利用堆栈计算 Ackerman函数
int P121_3_2(int m, int n)
{
	//[0]: m,[1]: n
	//[2]: 如果完成了计算,则是本层的f(m,n);
	//  如果没完成计算，则代表本层是怎么得到.2: 代表2式得到,  3:代表3式得到
	//[3]: 是否完成了计算
	int st[M][4], top = 0;
	st[0][0] = m;
	st[0][1] = n;
	st[0][3] = 0;
	while (top >= 0)
	{
		if (st[top][3] == 0) {
			// a:本层没有完成计算	
			if (st[top][0] == 0) {
				// (1)式,完成本层的计算,没必要再存m,n了
				// 此处不移动指针，指针移动在b处进行
				st[top][2] = st[top][1] + 1;
				st[top][3] = 1;
			}
			else if (st[top][1] == 0) {
				// (2)式
				// 此处需要进栈
				++top;
				st[top][0] = st[top - 1][0] - 1;
				st[top][1] = 1;
				st[top - 1][2] = 2;
				st[top][3] = 0;
			}
			else {
				// (3)式
				// 入栈子函数
				++top;
				st[top][0] = st[top - 1][0];
				st[top][1] = st[top - 1][1] - 1;
				st[top - 1][2] = 3;
				st[top][3] = 0;
			}
		}
		else if (top > 0 && st[top][3] == 1) {
			// b:本层已有结果
			// st[top][2]不可能==1,只可能是{2,3}
			if (st[top-1][2] == 2 || st[top - 1][2] == 4) {
				// (2)式得到,直接将当前结果赋值给上一个结果
				--top;
				st[top][2] = st[top+1][2];
				st[top][3] = 1;
			}
			else if (st[top - 1][2] == 3) {
				// (3)式
				// 3式得到的话需要再次入栈
				st[top][0] = st[top - 1][0] - 1;
				st[top][1] = st[top][2];
				st[top][3] = 0;
				// 这里需要把上一个元素的计算方式改成4
				// 用于在子函数计算完毕后，直接给上一个元素赋值，而不是再走一遍这里
				st[top - 1][2] = 4;
			}
		}
		if (top == 0 && st[top][3] == 1) {
			break;
		}
	}
	return st[top][2];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68