错排问题 （抽奖，发邮件）

错排概念：

错排问题百科

 n个有序的元素应有 n! 个不同的排列，如若一个排列使得所有的元素不在原来的位置上，则称这个排列为错排；有的叫重排。
 如，1 2的错排是唯一的，即2 1。1 2 3的错排有3 1 2，2 3 1。这二者可以看作是1 2错排，3分别与1、2换位而得的。

 

递推关系推导

为求其递推关系，分两步走：

第一步，考虑第n个元素，把它放在某一个位置，比如位置 k ，一共有n-1种放法；
第二步，考虑第k个元素，这时有两种情况：

1. 把它放到位置n，那么对于除n以外的 n-1 个元素，由于第 k 个元素放到了位置 n，所以剩下 n-2 个元素的错排即可，有种 D(n-2) 放法；
2. 第k个元素不放到位置n，这时对于这 n-1个元素的错排，有 D(n-1) 种放法。

综上得到 D(n) = (n-1) * ( D(n-2) + D(n-1) )

特殊地，D(1) = 0, D(2) = 1
此外：

还有几种错排生成算法：递归法， 基于字典序的筛选法和改进字典序法等有兴趣可以深入了解

 
 
 

例题

发邮件

牛客网—发邮件
用A、B、C…表示三份邮件，a、b、c …表示 n 个要发送的人。把错装的总数为记作
D(n)。假设把 A 错发给 b里了，包含着这个错误的一切错装法分两类:

1. 给 b 发送的 A 邮件，这时每种错发的 A->b 关系已经确定（其余部分都与 A、B、a、b 无关），应有 D(n - 2) 种错发法。
2. 给 b 发送 A、B 之外的一个邮件，这时实际是把 (除 A 之外的) n- 1 份邮件 B、C 发给 (除 b 以外的) n - 1个人 a、c… …，显然这时发错的方法有 D(n - 1) 种。

总之在 A 错发给 b 的情况之下，共有错装法D(n- 2)+ D(n- 1)种。

A 错发给 c，发给d… 的 n - 2 种错误之下，同样都有D(n- 1)+ D(n - 2)种错发法,因此D(n) = (n-1) [ D(n-2) + D(n-1) ]
特殊地，D(0) = 0, D(1) = 0, D(2) = 1

#include <iostream>
using namespace std;
// 错排
/* arr[1] = 0, arr[2] = 1;递推公式：arr[n] = (n-1)*(arr[n-1]+arr[n-1]); */
int main()
{
    long long arr[22] = {0, 0, 1};
    for(int i = 3; i < 21; ++i)
        arr[i] = (i-1) * (arr[i-1]+arr[i-2]);

    int n;
    while(cin >> n){
        cout << arr[n] << endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

 
 
 

年会抽奖

牛客网—年会抽奖

今年公司年会的奖品特别给力，但获奖的规矩却很奇葩：

1. 首先，所有人员都将一张写有自己名字的字条放入抽奖箱中；
2. 待所有字条加入完毕，每人从箱中取一个字条；
3. 如果抽到的字条上写的就是自己的名字，那么“恭喜你，中奖了！”
   现在告诉你参加晚会的人数，请你计算有多少概率会出现无人获奖？
   
   

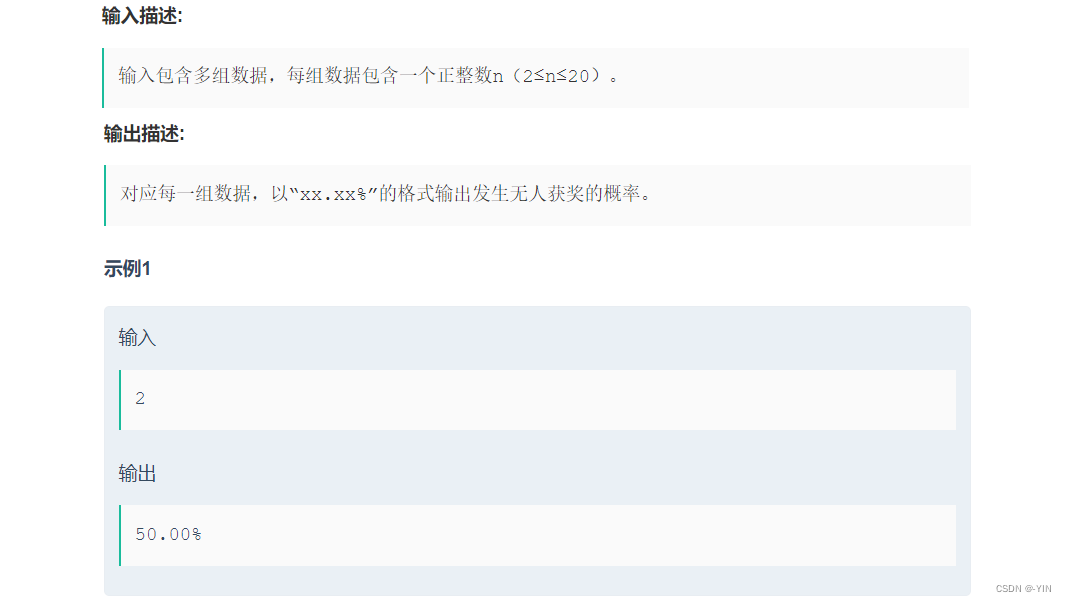
参考代码：

#include <iostream>
using namespace std;

// 递归计算错排序列个数
long long Derangement(int n){
    if(1 == n) return 0;
    if(2 == n) return 1;
    // 递推公式
    return (n-1)*(Derangement(n-2)+Derangement(n-1));
}

// 计算阶乘（所有可能的序列数）
long long factorial(int n){
    long long f = 1;
    for(int i = 1; i <= n; ++i)
        f *= i;
    return f;
}

int main()
{
    int n;
    while(cin >> n){
        double res = (double)Derangement(n) / factorial(n);
        printf("%.2lf%c\n",res*100, '%');  
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27