• 终于搞懂什么是动态规划的

    目录

    1.DP到底是个啥

    1.1 热身：如何说一万次“我爱你”

    2 路径连环炮

    第一炮：基本问题：统计路径总数

    第二炮：使用二维数组优化递归

    第三炮：滚动数组：用一维代替二维数组

    第四炮：题目拓展：最小路径和

    第五炮：题目拓展：三角形最小路径和

    3 理解动态规划

    DP问题在整个算法中的题目属于中上，大部分人可能接触了十年也没搞懂DP到底是什么。工作里貌似也没用到啊。为什么要一直考察这个呢，而且考察越来越多？主要是因为互联网开始卷了，算法是刷人最好的工具，让谁走，谁都无话可说。

    本章我们从基本问题出发逐步拓展，充分讲解与动态规划相关的几个关键问题，让你真正感受到”动态规划，不过如此“。之后给大家总结出动态规划的模板，是的，动态是有解题模板的。

    1.DP到底是个啥

    虽然谁都知道动态规划（Dynamic Programming，简称DP）难，但是没几个人能说清啥是DP。而且即使将DP的概念写出来也没几个人看懂到底啥意思。

    下面我们就从一个简单例子来逐步拆解这个复杂的解释。

    1.1 热身：如何说一万次“我爱你”

    首先来感受一下什么是重复计算和记忆化搜索。

    曾经参加过一次线上小活动，看谁说更多的“我爱你”，我当时写了这么一段代码：

    1. public class FibonacciTest {
    2.     public static int count = 0;
    3.     public static void main(String[] args) {
    4.         fibonacci(20);
    5.         System.out.println("count:" + count);
    6.     }
    7.     public static int fibonacci(int n) {
    8.         System.out.println("我爱你");
    9.          count++;
    10.         if (n == 0) {
    11.             return 1;
    12.         }
    13.         if (n == 1 || n == 2)
    14.             return n;
    15.         else {
    16.             return fibonacci(n - 1) + fibonacci(n - 2);
    17.         }
    18.     }
    19. }

    这个就是斐波那契数列，当n为20时，count是21891次。而当n=30 的时候结果是2692537，也就是接近270万。如果纯粹只是算斐波那契数列，我们可以直接循环：

    1.  public static int count_2 = 0;
    2. public int fibonacci(int n) {
    3.         if (n <= 2) {
    4.             count_2++;
    5.             return n;
    6.         }
    7.  
    8.         int f1 = 1;
    9.         int f2 = 2;
    10.         int sum = 0;
    11.         for (int i = 3; i <= n; i++) {
    12.             count_2++;
    13.             sum = f1 + f2;
    14.             f1 = f2;
    15.             f2 = sum;
    16.         }
    17.         return sum;
    18.     }

    n为30时也不过计算二十几个数的累加，但是为什么采用递归竟然高达270万呢？因为里面存在大量的重复计算，数越大，重复越多。例如当n=8的时候，我们看下面的结构图就已经有很多重复计算了：

     上面我们在计算f(8)时，可以看到f(6)、f(5)等等都需要计算，这就是重叠子问题。怎么对其优化一下呢？可以看到这里主要的问题是很多数据都会频繁计算，如果将计算的结果保存到一个一维数组里。把 n 作为我们的数组下标，f(n) 作为值，也就是 arr[n] = f(n)。执行的时候如果某个位置已经被计算出来了就更新对应位置的数组值，例如 f(4) 算完了，就将其保存到arr[4]中，当后面再次要计算 f(4) 的时候，我们判断f(4)已经计算过，因此直接读取 f(4) 的值，不再递归计算。代码如下：

    1. public static int[] arr = new int[50];
    2. public static int count_3 = 0;
    3. Arrays.fill(arr, -1);
    4. arr[0] = 1;
    5. int fibonacci(int n){
    6.         if (n == 2 || n == 1) {
    7.             count_3++;
    8.             arr[n] = n;
    9.             return n;
    10.         }
    11.  
    12.         if (arr[n] != -1) {
    13.             count_3++;
    14.             return arr[n];
    15.         } else {
    16.             count_3++;
    17.             arr[n] = fibonacci(n - 1) + fibonacci(n - 2);
    18.             return arr[n];
    19.         }
    20.     }

    在上面代码里，在执行递归之前先查数组看是否被计算过，如果重复计算了，就直接读取，这就叫”记忆化搜索“，就这么简单。

    2 路径连环炮

    要解释清楚DP，还要再结合一些实例来分析，本部分我们通过多个路径相关的问题来分析。路径问题本身就是大热门，同时其特点是易于画图，方便理解，能循序渐进展示DP的内涵。

    第一炮：基本问题：统计路径总数

    LeetCode62：一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ），问总共有多少条不同的路径？

    1. 示例1：
    2. 输入：m = 3, n = 7
    3. 输出：28
    4. 示例2：
    5. 输入：m = 3, n = 2
    6. 输出：3
    7. 解释：
    8. 从左上角开始，总共有 3 条路径可以到达右下角。
    9. 1. 向右 -> 向下 -> 向下
    10. 2. 向下 -> 向下 -> 向右
    11. 3. 向下 -> 向右 -> 向下

    本题是经典的递归问题，第一炮，我们来研究如何通过递归来解决此问题。如下图所示，从起点开始的每一个位置，要么向右，要么向下。每一种都将导致剩下的区间的减少了一行或者一列，形成两个不同的区间。而每个区间都可以继续以红点为起点继续上述操作，所以这就是一个递归的过程。

    图中红色表示起止点，绿色表示接下来要走的位置，灰色表示不能再走了。

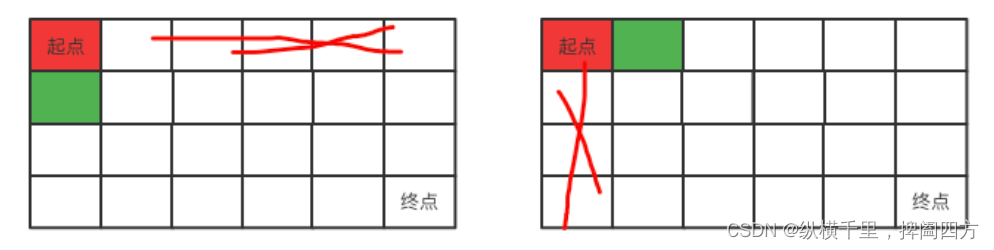
     我们先从一个3x2的情况来分析：

    我们的目标是从起点到终点，因为只能向右或者向下，从图中可以可以看到：

    1.如果向右走，也就是图1的情况，后面是一个3x1的矩阵，此时起点下面的两个灰色位置就不会再访问了，只能从绿色位置一直向下走，只有一种路径。

    2.如果是向下走，我们可以看到原始起点右侧的就不能再访问了，而剩下的又是一个2X2的矩阵，也就是从图中绿色位置到红色位置，此时仍然可以选择向右或者向下，一共有两种路径。

    所以上面的情况加起来就是一共有3种。

    从上面我们可以看到，对于一个3X2的矩阵，总的路径数就是从起点开始再分别统计arr一个2X2的数组和一个1X3的数组，之后累加起来就行了。如果再复杂一点，是一个3X3的矩阵呢？我们还是直接看图：

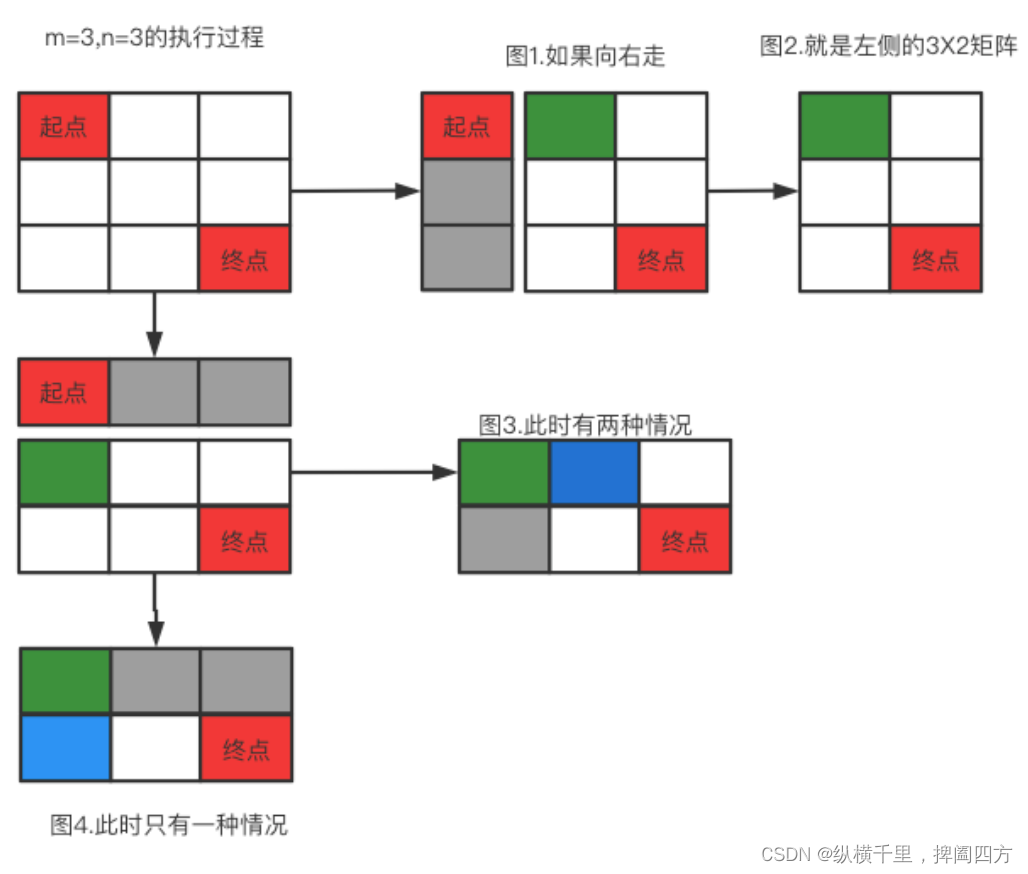
    可以看到，一个3X3的矩阵下一步就变成了一个3X2或者2X3的矩阵，而总路径数，也是是两者各自的路径之和。

    因此，对于一个mxn的矩阵，求路径的方法search(m,n)就是：

     search(m-1,n)+search(m,n-1);

     递归的含义就是处理方法不变，但是问题的规模减少了，所以这里的代码就是：

    1. public class Solution {
    2.    public int uniquePaths (int m, int n) {
    3.      return search(m,n);     
    4.   }
    5.    public int search(int m,int n){ 
    6.          if(m==1 || n==1){
    7.            return 1;
    8.       }
    9.       return search(m-1,n)+search(m,n-1);
    10.   }
    11. }

    上面这个过程，我们也可以用二叉树表示出来：

    例如对于3X3的矩阵，过程图就是：

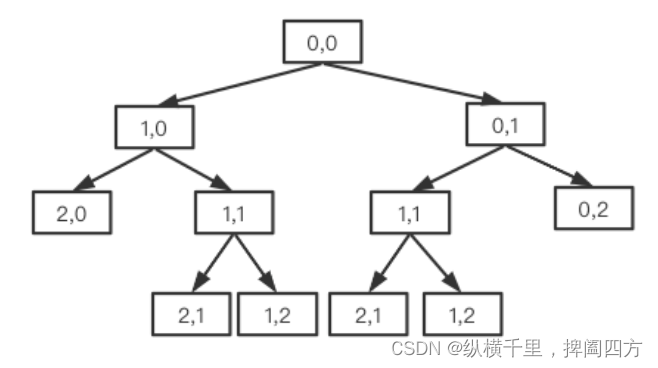
    而总的路径数就是叶子节点数，在图中是6个，这与二叉树的递归遍历本质上是一样的。

    第二炮：使用二维数组优化递归

    第二炮，我们来优化递归的问题，研究如何结合二维数组来实现记忆化搜索。

    从上面这个树也可以看到在递归的过程中存在重复计算的情况，例如{1,1}出现了两次，如果是一个NXN的空间，那{1,0}和{0,1}的后续计算也是一样的。

    从二维数组的角度，例如在位置(1,1)处，不管从(0,1)还是(1,0)到来，接下来都会产生2种走法，因此不必每次都重新遍历才得到结果。

     为此，我们可以采取一个二维数组来进行记忆化搜索，算好的就记录在数组中，也就是这样子：

    每个格子的数字表示从起点开始到达当前位置有几种方式，这样我们计算总路径的时候可以先查一下二维数组有没有记录，如果有记录就直接读，没有再计算，这样就可以大量避免重复计算，这就是记忆化搜索。

    根据上面的分析，我们可以得到两个规律：

    1.第一行和第一列都是1。

    2.其他格子的值是其左侧和上方格子之和。对于其他m，n的格子，该结论一样适用的，例如：

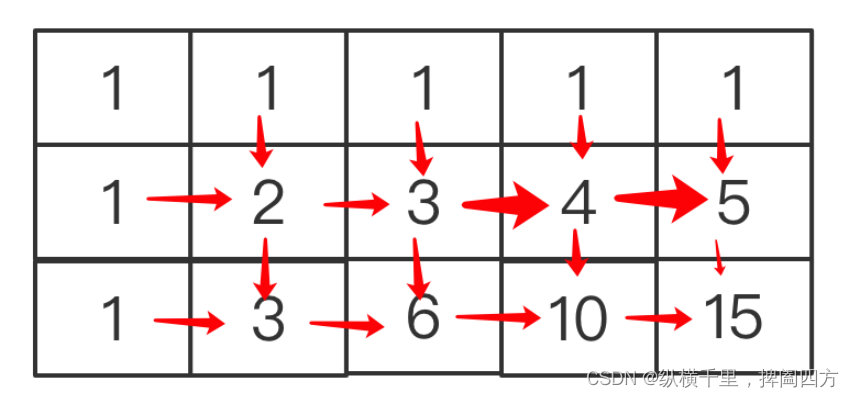
     比如图中的4，是有上面的1和左侧的3计算而来，15是上侧的5和左侧的10计算而来。如果用公式表示就是：

     我们可以直接写出如下代码：

    1. public int uniquePaths(int m, int n) {
    2.     int[][] f = new int[m][n];
    3.     f[0][0] = 1;
    4.     for (int i = 0; i < m; i++) {
    5.         for (int j = 0; j < n; j++) {
    6.          if (i > 0 && j > 0) {
    7.                f[i][j] = f[i - 1][j] + f[i][j - 1];
    8.             } else if (i > 0) {
    9.                 f[i][j] = f[i - 1][j];
    10.             } else if (j > 0) {
    11.                 f[i][j] = f[i][j - 1];
    12.              }
    13.          }
    14.     }
    15.     return f[m - 1][n - 1];
    16. }

    第三炮：滚动数组：用一维代替二维数组

    第三炮，我们通过滚动数组来优化此问题。上面的缓存空间使用的是二维数组，这个占空间太大了，能否进一步优化呢？

    我们再看一下上面的计算过程：

     在上图中除了第一行和第一列都是1外，每个位置都是其左侧和上访的格子之和，那我可以用一个大小为n的一维数组解决来：

     上面这几个一维数组拼接起来，是不是发现和上面的二维数组完全一样的？而这里我们使用了一个一维数组就解决了，这种反复更新数组的策略就是滚动数组.计算公式是：

    dp[j] = dp[j] + dp[j - 1]

    其实就是这么回事，代码如下：

    1.     public int uniquePaths(int m, int n) {
    2.         int[] dp = new int[n];
    3.         Arrays.fill(dp, 1);
    4.         for(int i = 1; i < m; ++i) {
    5.             for(int j = 1; j < n; ++j) {
    6.                 //等式右边的 dp[j]是上一次计算后的，加上左边的dp[j-1]即为当前结果
    7.                 dp[j] = dp[j] + dp[j - 1];
    8.             }
    9.         }
    10.         return dp[n - 1];
    11.     }

    这个题目涵盖了DP里的多个方面，比如重复子问题、记忆化搜索、滚动数组等等。这就是最简单的动态规划了，只不过我们这里的规划是dp[j] = dp[j] + dp[j - 1];不用进行复杂的比较和计算。

    这个问题非常重要，学好了对后面理解递归、动态规划等算法都有非常大的作用。

    第四炮：题目拓展：最小路径和

    上面的题目还有两个重要问题体现的不明显：最优子结构，我们再结合一个例子来研究。

    LeetCode64.给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

    说明：每次只能向下或者向右移动一步。示例：

    1. 输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
    2. 输出：7
    3. 解释：因为路径 1→3→1→1→1 的总和最小。

    这道题是在上面题目的基础上，增加了路径成本概念。由于题目限定了我们只能「往下」或者「往右」移动，因此我们按照当前位置可由哪些位置转移过来 进行分析：

    • 当前位置只能通过「往下」移动而来，即有f[i][j] = f[i-1][j] + grid[i][j]

    • 当前位置只能通过「往右」移动而来，即有 f[i][j] = f[i][j-1] + grid[i][j]

    • 当前位置既能通过「往下」也能「往右」移动，即有f[i][j] = min(f[i][j-1],f[i-1][j]) + grid[i][j]

    二维数组的更新过程，我们可以图示一下：

    我们现在可以引入另外一个概念状态：所谓状态就是下面表格更新到最后的二维数组,而通过前面格子计算后面格子的公式就叫状态转移方程。如果用数学表达就是：

    定义 f[i][j]为从 (0,0) 开始到达位置 (i,j)的最小总和。那么 f[m-1][n-1]就是我们最终的答案，f[0][0]=grid[0][0]是一个显而易见的起始状态。

    如果令f[i][j]表示从f(0,0)走到格子(i,j)的路径的最小数字总和，则使用表达式来表示上面的关系就是：

    所谓的确定状态转移方程就是要找递推关系，通常我们会从分析首尾两端的变化规律来入手，后面题目我们会继续分析。

    本题的代码实现就是： 

    1. public int minPathSum(int[][] grid) {        
    2.         int m = grid.length, n = grid[0].length;
    3.         int[][] f = new int[m][n];
    4.         for (int i = 0; i < m; i++) {
    5.             for (int j = 0; j < n; j++) {
    6.                 if (i == 0 && j == 0) {
    7.                     f[i][j] = grid[i][j];
    8.                 } else {
    9.                     int top  = i - 1 >= 0 ? f[i - 1][j] + grid[i][j] : Integer.MAX_VALUE;
    10.                     int left = j - 1 >= 0 ? f[i][j - 1] + grid[i][j] : Integer.MAX_VALUE;
    11.                     f[i][j] = Math.min(top, left);
    12.                 }
    13.             }
    14.         }
    15.         return f[m - 1][n - 1];
    16.     }

    第五炮：题目拓展：三角形最小路径和

    本题是上面一条的简单变型，LeetCode120.给定一个三角形 triangle ，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

    1. 示例1：
    2. 输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
    3. 输出：11
    4. 解释：如下面简图所示：
    5.    2
    6.   3 4
    7.  6 5 7
    8. 4 1 8 3
    9. 自顶向下的最小路径和为 11（即2 + 3 + 5 + 1 = 11）。

    在看解析之前，我们先看一下这个题是什么意思。本题就是1.2中最小路径和的简单变换，

    为了方便处理，我们可以先处理成对角线结构。

    如果上面的图你能想明白，就可以直接写代码了 ， 但是我们想通过本题我们来理解另外一个概念”无后效性“，确定一道题目是否可以用 DP 解决，要从有无后效性进行分析。所谓无后效性就是我们转移某个状态需要用到某个值，但是并不关心该值是如何而来的。更加装*的表述是：当前某个状态确定后，之后的状态转移与之前的决策无关，因此我们可以确定使用 DP 进行求解。 

    在本题中，既然是从上到下的路径，那么最后一个点必然落在最后一行。对于最后一行的某个位置的值，根据题意只能从上一行的某一个位置或者某两个位置之一转移而来。同时，我们只关注前一位的累加值是多少，特别是最小累加值是多少，而不关心这个累加值结果是由什么路径而来的，这就满足了「无后效性」的定义。

    接下来的问题是该如何确定「状态定义」呢？这就是要找递推关系，通常会从首尾两端的变化规律来入手。对于本题，我们结合两者可以猜一个 DP 状态：f[i][j]代表到达某个点的最小路径和，那么 min(f[n-1][i])（最后一行的每列的路径和的最小值）就是答案。

    通过观察可以发现以下性质（令 i 为行坐标，j 为列坐标）：

    • 每一行 i具有 i+1个数字(i从0开始)

    • 只要不是第一列（j!=0）位置上的数，都能通过「左上方」转移过来

    • 只要不是每行最后一列（j!=i）位置上的数，都能通过「上方」转移而来

    该过程可以推广并覆盖所有位置的，至此，状态转移方程也能不重不漏的枚举到每一条路径，因此这个 DP 状态定义可用，代码：

    1. public int minimumTotal(List<List<Integer>> tri) {
    2.         int n = tri.size();
    3.         int ans = Integer.MAX_VALUE;
    4.         int[][] f = new int[n][n];
    5.         f[0][0] = tri.get(0).get(0);
    6.         for (int i = 1; i < n; i++) {
    7.             for (int j = 0; j < i + 1; j++) {
    8.                 int val = tri.get(i).get(j);
    9.                 f[i][j] = Integer.MAX_VALUE;
    10.                 if (j != 0) {
    11.                     f[i][j] = Math.min(f[i][j], f[i - 1][j - 1] + val);
    12.                  }
    13.                 if (j != i){
    14.                      f[i][j] = Math.min(f[i][j], f[i - 1][j] + val);
    15.                 } 
    16.             }
    17.         }
    18.         for (int i = 0; i < n; i++){
    19.         ans = Math.min(ans, f[n - 1][i]);
    20.         } 
    21.         return ans;
    22.     }

    与本题非常类似的题目还有LeetCode931题”下降路径最小和“，以及LeetCode1289题”下降路径最小和II“，感兴趣的同学可以研究一下。

    3 理解动态规划

    经过上面这么多例子，我们终于可以完整的分析什么是动态规划了。

    首先，DP能解决哪类问题？直观上，DP一般是让找最值的，例如最长公共子序列等等，但是最关键的是DP问题的子问题不是相互独立的，如果递归分解直接分解会导致重复计算指数级增长(想想前面的热身题)。而DP最大的价值是为了消除冗余，加速计算。

    其次，严格来说，DP要满足「有无后效性」，也就是能进行“狗熊掰棒子，只管当下，不管之前”，对于某个状态，我们可以只关注状态的值，而不需要关注状态是如何转移过来的话，满足该要求的可以考虑使用 DP 解决。 为了理解这一点，我们来看一下这个问题：

    上面路径的问题，从左上角走到右下角，我们设置两个问题，请问哪个是动态规划问题：

    A 求有多少种走法 B 输出所有的走法

    我们说动态规划是无后向型的，只记录数量，不管怎么来的，因此A是DP问题，而B不能用DP。如果你理解上一章回溯的原理的话，就知道回溯可以记录所有的路径，因此B是个回溯的问题。

    回溯：能解决，但是解决效率不高

    DP：计算效率高，但是不能找到满足要求的路径。

    因此区分动态规划和回溯最重要的一条是： 动态规划只关心当前结果是什么，怎么来的就不管了，所以动态规划无法获得完整的路径，这与回溯不一样，回溯能够获得一条甚至所有满足要求的完整路径。

    DP的基本思想是将待求解问题分解成若干个子问题，先求子问题，再从这些子问题中得到原问题的解。既然要找“最”值那必然要做的就是穷举来找所有的可能，然后选择“最”的那个，这就是为什么在DP代码中大量判断逻辑都会被套上min()或者max()，而这也是导致DP看起来很难的原因之一。

    接下来，既然穷举，那为啥还要有DP的概念？这是因为穷举过程中存在大量重复计算，效率低下，所以我们要使用记忆化搜索等方式来消除不必要的计算，所谓的记忆化搜索就是将已经计算好的结果先存在数组里，后面直接读就不再重复计算了。

    接下来，既然记忆化能解决问题，为啥DP这么难，因为DP问题一定具备“最优子结构”，这样才能让记忆时得到准确的结果。至于什么是最优子结构，我们还是要等后面具体问题再看。

    接下来，有了最优子结构之后，我们还要写出正确的“状态转移方程”，才能正确的穷举。也就是递归关系，但是在DP里，大部分递推都可以通过数组实现，因此看待的代码结构一般是这样的for循环，这就是DP代码的基本模板：

    1.    //   初始化base case，也就是刚开始的几种场景 ，有几种枚举几种
    2.         dp[0][0][...]=base case
    3.     //  进行状态转移
    4.         for 状态1 状态1的所有取值
    5.             for 状态2 in 状态2的所有取值
    6.                for ....
    7.                  dp[状态1][状态2][...]=求最值Max(选择1，选择2,...)
    8.     }

    我们一般写的动态规划只有一两层，不会太深，因此你会发现动态规划的代码特别简洁。

    动态规划的常见类型也比较多，从形式上看，有坐标型、序列型、划分型、区间型、背包型和博弈型等等。不过没必要刻意研究这些类型到底什么意思，因为解题基本思路是一致的。一般说来，动态规划题目有以下三种基本的类型：

    1.计数有关，例如求有多少种方式走到右下角，有多少种方式选出K个数使得***等等，而不关心具体路径是什么。

    2.求最大最小值，最多最少等等，例如最大数字和、最长上升子序列长度、最长公共子序列、最长回文序列等等。

    3.求存在性，例如取石子游戏，先手是否必胜；能不能选出K个数使得**等等。

    但是不管哪一种解决问题的模板也是类似的，都是：

    • 第一步：确定状态和子问题，也就是枚举出某个位置所有的可能性，对于DP，大部分题目分析最后一步更容易一些，得到递推关系，同时将问题转换为子问题。

    • 第二步：确定状态转移方程，也就是数组要存储什么内容。很多时候状态确定之后，状态转移方程也就确定了，因此我们也可以将第一二步作为一个步骤。

    • 第三步：确定初始条件和边界情况，注意细心，尽力考虑周全。

    • 第四步：按照从小到大的顺序计算：f[0]、f[1]、f[2]...

    虽然我们计算是从f[0]开始，但是对于大部分的DP问题，先分析最后一个往往更有利于寻找状态表达式，因此我们后面的问题基本都是

    从右向左找递归，从左向右来计算

    这个也是我们分析DP问题的核心模板。

    上面的模板，用大白话就是：我们要自始至终，都要在大脑里装一个数组，要看这个数组每个元素表示的含义是什么，要看每个数组位置是根据谁来算的，然后就是从小到大挨着将数组填满，最后看哪个位置是我们想要的结果。

    再详细一点的解释：

    我们要自始至终，都要在大脑里装一个数组（可能是一维，也可能是二维），要看这个数组每个元素表示的含义是什么（也就是状态），要看每个数组位置是根据谁来算的(状态转移方程)，然后就是从小到大挨着将数组填满(从小到大计算,实现记忆化搜索)，最后看哪个位置是我们想要的结果。

  • 相关阅读:
    快手根据ID取商品详情 API 返回值说明
    快速排序【C语言数据结构】
    什么是VR应急预案演练虚拟化|VR体验馆加盟|元宇宙文旅
    将nestjs项目迁移到阿里云函数
    Java“牵手”速卖通商品列表页数据采集+速卖通商品价格数据排序，速卖通API接口申请指南
    【Wio Terminal】使用WiFi（3）- Wi-F的高级使用
    bwapp下载安装
    关于ubuntu开发环境配置
    aspnetcore6.0源代码编译调试
    ⚡文件工具类⚡
  • 原文地址：https://blog.csdn.net/xueyushenzhou/article/details/125548959