数学建模算法与应用：预测模型（2）灰色预测模型

目录

前言

         GM（1，1）预测模型

1.GM（1，1）模型预测方法 

2.GM(1，1)模型预测步骤

        （1）数据的检验与处理 

        （2）建立模型 

        （3）检验预测值 

3.GM（1，1）模型预测实例

 (1）级比检验：建立交通噪声平均声级数据时间序列如下：

 (2)GM(1，1)建模

(3)模型检验 

4.MATLAB模型程序 

---

前言

        灰色预测的主要特点是模型使用的不是原始数据序列，而是生成的数据序列。其核心体系是灰色模型（ Grey Model ，简称 GM )，即对原始数据作累加生成（或其它方法生成）得到近似的指数规律再进行建模的方法。优点是不需要很多的数据，一般只需要4个数据就够，能解决历史数据少、序列的完整性及可靠性低的问题；能利用微分方程来充分挖掘系统的本质，精度高；

         能将无规律的原始数据进行生成得到规律性较强的生成序列，运算简便，易于检验，具有不考虑分布规律，不考虑变化趋势。缺点是只适用于中短期的预测，只适合指数增长的预测。

         GM（1，1）预测模型

        GM（1，1）表示模型是一阶微分方程，且只含1个变量的灰色模型。 

1.GM（1，1）模型预测方法 

        定义1：已知参考数据列： ，一次累加生成序列(1-AGO)

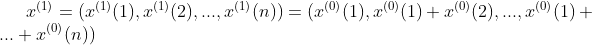
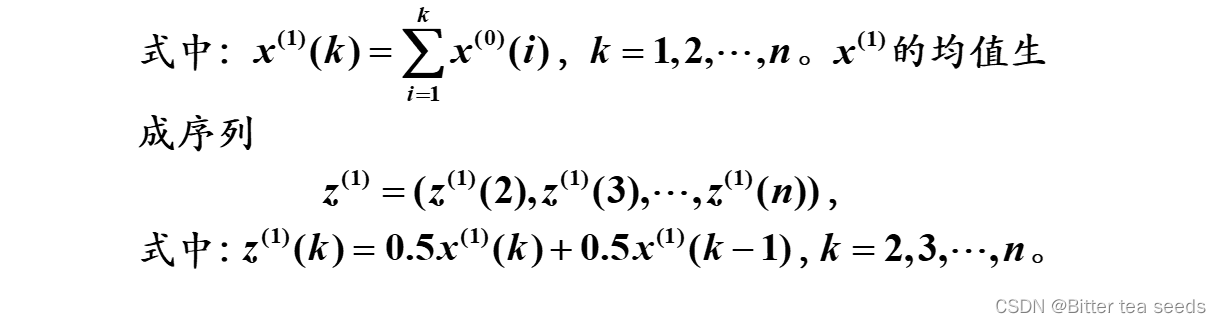
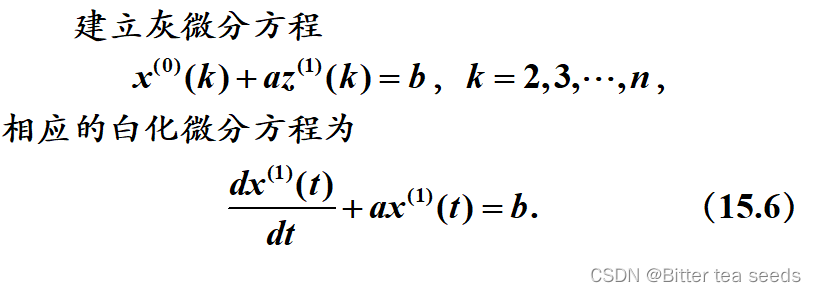
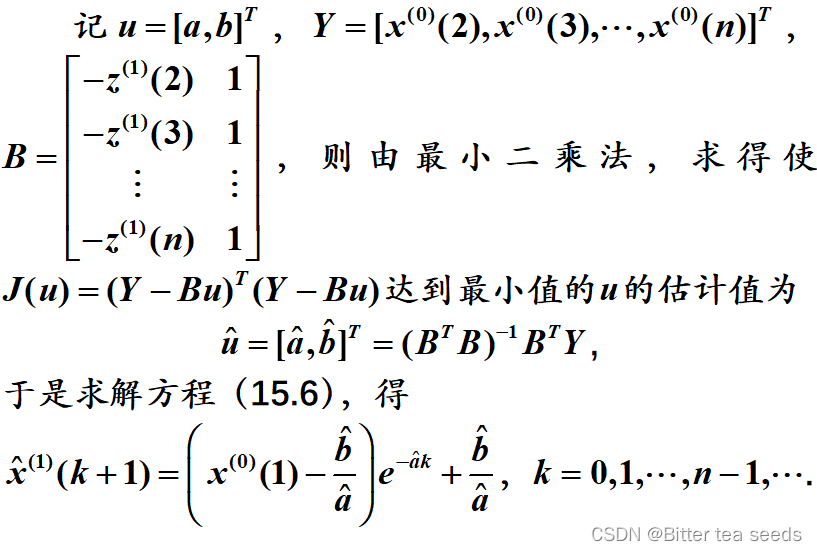
2.GM(1，1)模型预测步骤

        （1）数据的检验与处理 

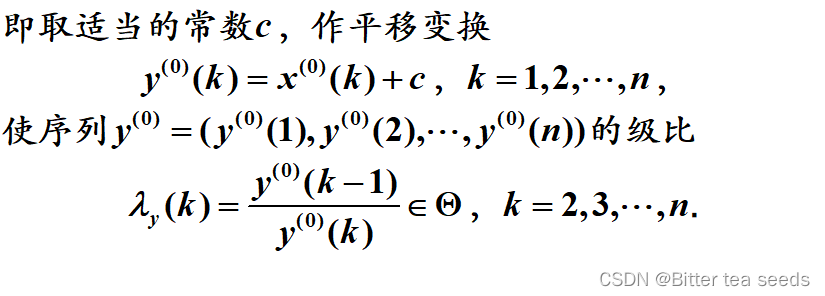
        （2）建立模型 

        （3）检验预测值 

3.GM（1，1）模型预测实例

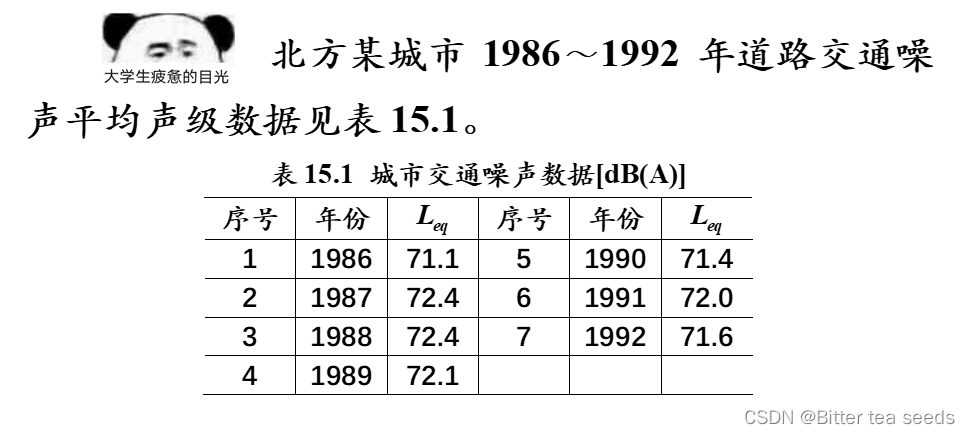
 (1）级比检验：建立交通噪声平均声级数据时间序列如下：

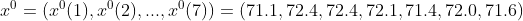
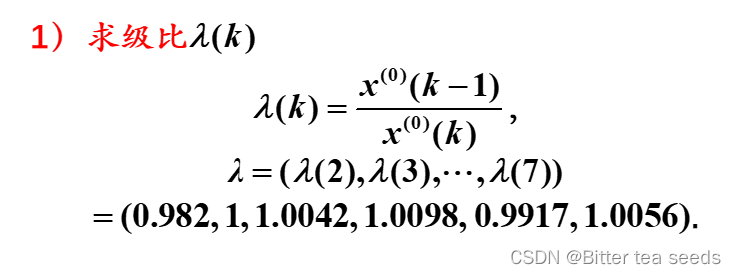
 (2)GM(1，1)建模

1）对原始数列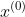作一次累加，得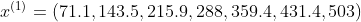

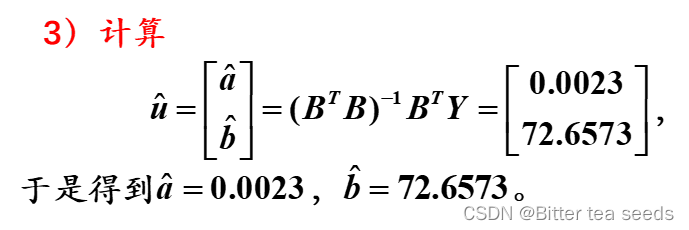
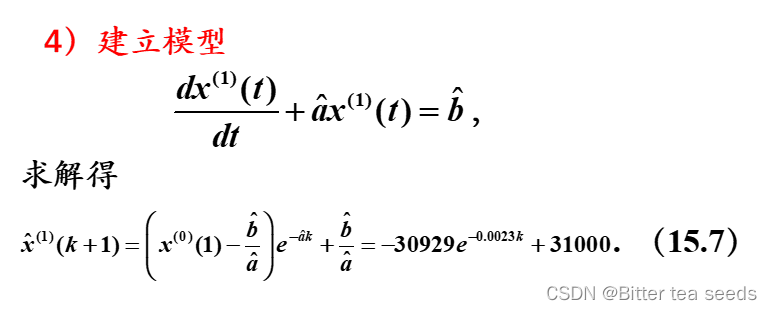
         5）求生成序列预测值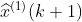及模型还原值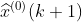，令k=1,2,3,4,5,6;

由式（15.7）的时间响应函数可计算得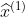，其中取,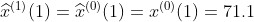

由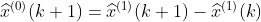，取k=1,2,3,4,5,6,得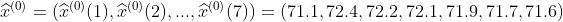

         

(3)模型检验 

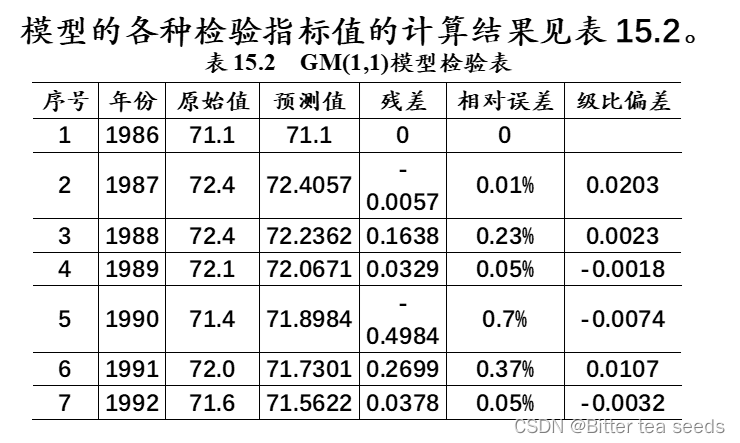
         经验证，该模型的精度较高，可以进行预测和预报。

4.MATLAB模型程序 

 代码如下，所示：

x0=[71.1 72.4 72.4 72.1 71.4 72.0 71.6]'; %注意这里为列向量
n=length(x0);
lamda=x0(1:n-1)./x0(2:n)  %计算级比
range=minmax(lamda')  %计算级比的范围
x1=cumsum(x0)  %累加运算
B=[-0.5*(x1(1:n-1)+x1(2:n)),ones(n-1,1)];
Y=x0(2:n);
u=B\Y  %拟合参数u(1)=a,u(2)=b
syms x(t)
x=dsolve(diff(x)+u(1)*x==u(2),x(0)==x0(1)); %求微分方程的符号解
xt=vpa(x,6) %以小数格式显示微分方程的解
yuce1=subs(x,t,[0:n-1]); %求已知数据的预测值
yuce1=double(yuce1); %符号数转换成数值类型，否则无法作差分运算
yuce=[x0(1),diff(yuce1)]  %差分运算，还原数据
epsilon=x0'-yuce    %计算残差
delta=abs(epsilon./x0')  %计算相对误差
rho=1-(1-0.5*u(1))/(1+0.5*u(1))*lamda'  %计算级比偏差值，u(1)=a

 结果：

 
lamda =
 
     711/724   
       1       
     724/721   
     103/102   
     119/120   
     180/179   
 
 
range =
 
     711/724        103/102   
 
 
x1 =
 
     711/10    
     287/2     
    2159/10    
     288       
    1797/5     
    2157/5     
     503       
 
 
u =
 
      50/21333 
   15476/213   
 
 
xt =
 
31000.0 - 30928.9*exp(-0.00234379*t)
 
 
yuce =
 
  1 至 5 列
 
     711/10        4996/69        9174/127      10738/149       9203/128   
 
  6 至 7 列
 
    4519/63       13239/185   
 
 
epsilon =
 
  1 至 5 列
 
       0            -29/5051      1523/9300       121/3681      -472/947   
 
  6 至 7 列
 
     790/2927        89/2353  
 
 
delta =
 
  1 至 5 列
 
       0             13/163931      89/39347       18/39481       67/9598  
 
  6 至 7 列
 
      17/4535        41/77612 
 
 
rho =
 
  1 至 5 列
 
      62/3061        25/10679      -11/6077       -61/8199       171/16049 
 
  6 列
 
     -36/11137 
 
>>